2021 江苏省赛

2021 江苏省赛

2024-2025 Winter Training Match B (Div.1)

GYM

5小时单挑，前 2h 依次过了 AICKJ，3.5h 出 D。H 最后 20min 出思路，没写完，结束后出的 H。

第一次写这种做题记录博客，就是趁着有空记录一下场上怎么想的，会写一些关键思路，可能不会很详细。

后续补了后面的题会再往这里写。

A - Spring Couplets

纯签到，直接模拟

5分钟 看题 + 写完这一坨 + 一发过

const int N = 1e5 + 32;
ll n, m, k;
ll a[N], b[N];

int main()
{
    ll T = re;
    while(T--)
    {
        n = re;
        fr(i, 1, n)
        {
            string s;
            cin >> s;
            int len = s.size();
            int ch = s[len-1] - '0';
            a[i] = ch;
        }
        fr(i, 1, n)
        {
            string s;
            cin >> s;
            int len = s.size();
            int ch = s[len-1] - '0';
            b[i] = ch;
        }
        if(a[n] == 1 || a[n] == 2)
        {
            puts("NO");
            continue;
        }

        bool ok = 1;
        fr(i, 1, n)
        {
            if(a[i] == 1||a[i]==2)
            {
                if(b[i]==1||b[i]==2) ok = 0;
            }

            if(a[i]==3||a[i]==4)
            {
                if(b[i] ==3||b[i]==4) ok=0;
            }
        }
        if(ok == 0) puts("NO");
        else puts("YES");
    }
    return 0;
}   

I - Fake Walsh Transform

发现所有的数异或起来是 0，只要再异或一下 n 就能得到 n 了。

WA 了两发，因为 \(m=1\) 要特判。

const int N = 1e5 + 32;
ll n, m, k;

int main()
{
    ll T = re;
    while(T--)
    {
        m = re, n = re;
        if(m == 1)
        {
            if(n == 0) puts("1");
            if(n == 1) puts("2");
            continue;
        }
        ll ans = (1LL << m);
        // ans -= __builtin_popcountll(n);
        if(n != 0) --ans;
        W(ans, '\n');
    }
    return 0;
}   

C - Magical Rearrangement

每次贪心地放最小的数，放的时候判断一下放完这个数剩下的数能否合法被放置，如果不行，就说明这个数不能放，要放更大的。如果 \(0 \sim 9\) 都放不了，就说明不合法。

设数字 \(i\) 剩余的个数为 \(a[i]\)，当前要放的数为 \(k\)，所有未放的数（包含要放的这个 \(k\)）的个数为 \(su\)，即 \(su=\sum a[i]\)

对于每个 \(i\)，当 \(i \neq k\) 时，需要满足 \(su-a[i] \geq a[i]\)；当 \(i = k\) 时，需要满足 \(su-a[i]\geq a[i]-1\)。

代码能力。

const int N = 1e5 + 32;
ll n, m, k;
ll a[20];

bool Check(ll x)
{
    ll su = 0;
    fr(i, 0, 9)
    {
        su += a[i];
    }

    fr(i, 0, 9)
    {
        ll sheng = su - a[i];
        if(a[i] == 0) continue;
        if(i == x)
        {
            if(sheng < a[i]-1) return 0;
        }
        else
        {
            if(sheng-1 < a[i]-1) return 0;
        }
    }
    return 1;
}

int main()
{
    ll T = re;
    while(T--)
    {
        string ans = "";
        ll n = 0;
        fr(i, 0, 9) a[i] = re, n += a[i];

        if(n == 1 && a[0] == 1)
        {
            puts("0");
            continue;
        }

        int tot = 0;
        bool ok = 1;
        ll lst = 0;
        while(1)
        {
            ++tot;
            if(tot > n) break;
            bool ook = 0;
            fr(i, 0, 9)
            {
                if(i == lst) continue;
                if(a[i] == 0) continue;
                if(Check(i)) 
                {
                    ans.push_back(i+'0');
                    // cout<<i;
                    lst = i;
                    --a[i];
                    ook = 1;
                    break;
                }
            }
            if(ook == 0)
            {
                ok = 0;
                break;
            }
        }

        if(ok == 0) puts("-1");
        else
        {
            for(auto x : ans) cout<<x;
            puts("");
        }

    }
    return 0;
}   

K - Longest Continuous 1

好像比 C 简单不少。

在纸上画画就能直接发现规律，每次使答案+1的位置就是每个 \(2^i\) 这个数的最高位。

预处理出每个使答案变更的位置，然后用 upper_bound 二分查找 \(k\) 属于哪里，下标就是答案。

const int N = 1e6 + 32;
ll n, m, k;
ll a[N];

int main()
{
    a[1] = 2, a[2] = 3;
    ll mul = 2;
    for(ll i = 3; ; ++i)
    {
        ll x = i-1;
        a[i] = a[i-1] + x*mul;
        mul *= 2;

        if(a[i] > 2e9) 
        {
            n=i;
            break;
        }
    }    
    // fr(i, 1, 4) W(a[i], '\n');

    ll T = re;
    while(T--)
    {
        ll k = re;
        ll xia = upper_bound(a+1, a+n+1, k) - a;
        W(xia-1, '\n');
    }
    return 0;
}   

J - Anti-merge

刚开始读题的时候看见什么上下合并左右合并，什么玩意儿，题都没往下看就开始想怎么合并。读完题发现根本就不用合并。

读完题发现就是一个纯染色，\(tag\) 的种类最多有 1 种，每个连通块中元素个数除以 2 向下取整就是几个 \(tag\)。

dfs 的时候顺便存一下位置就行。

const int N = 600 + 32;
ll n, m, k;
ll a[600][600];
bool vis[N][N];
// ll 
ll dx[4] = {0,0,1,-1};
ll dy[4] = {1,-1,0,0};

struct node
{
    ll x, y;
};

vector<node> l, r, ans;

void dfs(ll x, ll y, ll now, ll k)
{
    if(k == 0) l.push_back({x, y});
    else r.push_back({x, y});
    fr(i,0,3)
    {
        ll nx = x+dx[i], ny = y+dy[i];
        if(nx <= 0 || ny <= 0 || nx > n || ny > m) continue;
        if(vis[nx][ny]) continue;
        if(a[nx][ny] != now) continue;
        vis[nx][ny] = 1;
        dfs(nx, ny, now, k^1);
    } 
}

int main()
{
    n = re, m = re;
    fr(i, 1, n)
        fr(j, 1, m)
            a[i][j] = re;

    fr(i, 1, n)
    {
        fr(j, 1, m )
        {
            if(vis[i][j] == 0)
            {
                vis[i][j] = 1;
                l.clear();
                r.clear();
                dfs(i, j, a[i][j], 0);

                if(l.size() <= r.size()) // l
                {
                    for(auto x : l) ans.push_back(x);
                }
                else
                {
                    for(auto x : r) ans.push_back(x);
                }
            }
        }
    }

    if(ans.size() == 0)
    {
        puts("0 0");
        return 0;
    }
    W(1, ' ');
    W(ans.size(), '\n');
    for(auto x : ans)
    {
        W(x.x, ' ');
        W(x.y, ' ');
        W(1, '\n');
    }
    return 0;
}   

D - Pattern Lock

很好玩的构造。在纸上画了一个小时，尝试了好多，最后画出来了一个靠谱的思路。

难点：每一组之间的衔接处，要满足小于90度。

每两列每两列一组，如果 \(m\) 是偶数，可以这样（与 \(n\) 的奇偶性无关）：

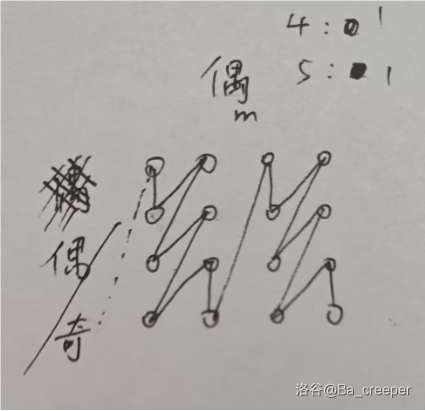
如果 \(m\) 是奇数，最后一定剩下 3 列，这时候对 \(n\) 分奇偶讨论。

\(n\) 是偶数的情况：

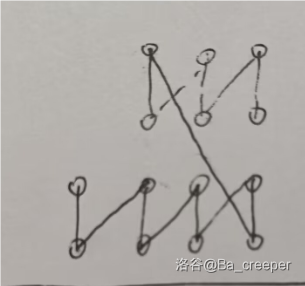
\(n\) 是奇数的情况，最后一定剩下一个 3x3：

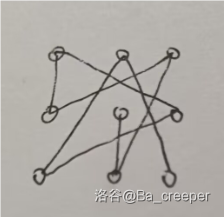
这样就做完了。每一部分之间的衔接处都小于 90 度。

const int N = 1e5 + 32;
ll n, m, k;

void _3(ll x, ll y) // 3x3
{
    W(x, y);
    W(x+1, y);
    W(x-1, y+1);
    W(x, y-1);
    W(x-1,y-1);
    W(x,y+1);
    W(x+1,y-1);
    W(x-1,y);
    W(x+1,y+1);
}

int main()
{
    n = re, m = re;

    ll lx = -1, ly = -1;
    for(int j = 1; j <= ((m-2)/2) * 2; j += 2)
    {
        W(1, j);
        fr(i, 2, n)
        {
            W(i, j);
            W(i-1, j+1);
        }
        W(n, j+1);
    }

    if(m%2 == 0)
    {
        ll j = m-1;
        W(1, j);
        fr(i, 2, n)
        {
            W(i, j);
            W(i-1, j+1);
        }
        W(n, j+1);
        return 0;
    }

    if(n%2 == 0)
    {
        for(int i = n-1; i>= 1; i -= 2)
        {
            W(i, m-2);
            fr(j, m-1, m)
            {
                W(i+1, j-1);
                W(i, j);
            }
            W(i+1, m);
        }
        return 0;
    }
    else
    {
        for(int i = n-1; i > 3; i -= 2)
        {
            W(i, m-2);
            fr(j, m-1, m)
            {
                W(i+1, j-1);
                W(i, j);
            }
            W(i+1, m);
        }
        _3(2, m-1);
        return 0;
    }

    return 0;
}   

H - Reverse the String

要翻转的区间的左端点可以确定：把原串的字符排序，从左往右扫，第一个与原串不同的就是左端点。

之后遍历右端点，问题转换成判断当前的右端点是否比之前的最优情况要优。

设之前最优情况右端点的位置为 \(now\)，当前右端点为 \(i\)，需要找到最大的 \(len\)，使串 \(s[now-len+1, now]=s[i-len+1,i]\)。

之后比较 \(s[now-len] 和 s[i-len]\) 两个字符的大小即可。

找最大的 len 可以二分，判断串相等用字符串哈希。

别忘特判初始串就是最优的情况。

const int N = 1e6 + 32;
ll n, m, k;

char ch[N], pai[N];

unsigned long long b[N], h[N];
unsigned long long b2[N], h2[N];

ll Check(ll l, ll r, ll L, ll R)
{
    ll x = (h[r] - h[l - 1] * b[r - l + 1]), y = (h[R] - h[L - 1] * b[R - L + 1]);
    ll x2 = (h2[r] - h2[l - 1] * b2[r - l + 1]), y2 = (h2[R] - h2[L - 1] * b2[R - L + 1]);
    return (x==y) && (x2 == y2);
}

int main()
{
    unsigned long long base1 = 13331;
    unsigned long long base2 = 131;
    ll T = re;
    while(T--)
    {
        b[0] = 1;
        b2[0] = 1;

        string s;
        cin >> s;

        n = s.size();

        fr(i, 0, n-1)
        {
            ch[i+1] = s[i];
            pai[i+1] = ch[i+1];
        }
        sort(pai+1, pai+n+1);
        ll l = -1;

        fr(i, 1, n)
        {
            if(pai[i] != ch[i])
            {
                l = i;
                break;
            }
        }

        if(l == -1)
        {
            cout<<s<<'\n';
            fr(i,0,n) b[i]=h[i]=0,ch[i]=pai[i]=0, b2[i]=h2[i] = 0;
            continue;
        }
        // W(l, '\n');

        ll now = l;

        for(int i = 1; i <= l; ++i)
        {
            b[i] = b[i - 1] * base1;
            h[i] = h[i - 1] * base1 + ch[i] - 'a' + 1;
            b2[i] = b2[i - 1] * base2;
            h2[i] = h2[i - 1] * base2 + ch[i] - 'a' + 1;
        }

        fr(i, l+1, n)
        {
            b[i] = b[i - 1] * base1;
            h[i] = h[i - 1] * base1 + ch[i] - 'a' + 1;
            b2[i] = b2[i - 1] * base2;
            h2[i] = h2[i - 1] * base2 + ch[i] - 'a' + 1;

            ll le = 0, rr = now - l + 1;
            ll mid;
            while(le<rr)
            {
                mid=(le+rr)/2+1;

                if(Check(now-mid+1, now, i-mid+1, i)) le=mid; 
                else rr=mid-1;
            }
            // le;
            if(le == now - l + 1)
            {
                int tot = 0;
                fr(j, now+1, i)
                {
                    ++tot;
                    int k = i-le+1-tot;
                    if(ch[j] == ch[k]) continue;
                    if(ch[j] > ch[k]) now = i;
                    break;
                }
                // now = i;
                continue;

            }
            if(ch[i-le] < ch[now-le]) now = i;
            // W(now, '\n');
        }
        // W(now, '\n');
        fr(i, 1, l-1) putchar(ch[i]);
        rp(i, now, l) putchar(ch[i]);
        fr(i, now+1, n) putchar(ch[i]);
        puts("");

        fr(i,0,n) b[i]=h[i]=0, ch[i]=pai[i]=0, b2[i]=h2[i] = 0;;
    }
    return 0;
}