[ZJOI2007]棋盘制作题解 & 悬线法

题意简述

给定 \(n \times m\) 的 01矩阵，从中找到最大的正方形和矩形使得 01 交错。

解题思路

采用悬线法。

悬线法

即对于每一行的状态，用一根横着的线左右移动，直到不满足条件或者到达边界为止，线的两端即为符合要求的区间。

定义状态

$ L[i][j] $ 表示从 \((i, j)\) 能到达的最左位置。
$ R[i][j] $ 表示从 \((i, j)\) 能到达的最右位置。
$ up[i][j] $ 表示 \((i, j)\) 能向上扩展多少层（包括自己这一层）。

初始化

假如只有自己，自己能到达的最左最右位置只有自己这儿；自己只有一层。

• \(L[i][j] = j;\)
• \(R[i][j] = j;\)
• \(up[i][j] = 1;\)

状态转移

一行中的不同列

枚举 \(j\)：

对于 \(L\)，仅当第 \(j\) 位能由 \(j - 1\) 扩展过来:

• \(L[i][j] = L[i][j - 1];\)

对于 \(R\)，仅当第 \(j\) 位能由 \(j + 1\) 扩展过来:

• \(R[i][j] = R[i][j + 1];\)

每行之间

仅当 \((i, j)\) 能与 \((i - 1, j)\) 联通，即 \((i, j)\) 能由 \((i- 1, j)\) 扩展过来时：

• $L[i][j] = max(L[i][j], L[i - 1][j]); $
• $R[i][j] = min(R[i][j], R[i - 1][j]); $
• \(up[i][j] = up[i - 1][j] + 1．\)

假设下图中绿色的方块为 $(i, j) $，那么红色的方块即为 $(i - 1, j) $。

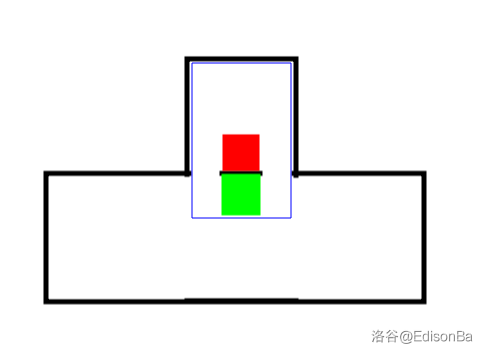
原来的 \(L[i][j]\) 较大，更新状态之后反而变小了。因为更新之后，$L[i][j] $ 代表的是蓝色方框内 $(i, j) $ 能到达的最左位置。\(R[i][j]\) 同理。

那可能有人有疑问了，要按照这样转移，最后是不是只考虑了下图蓝色的部分？可是答案是绿色的部分啊？

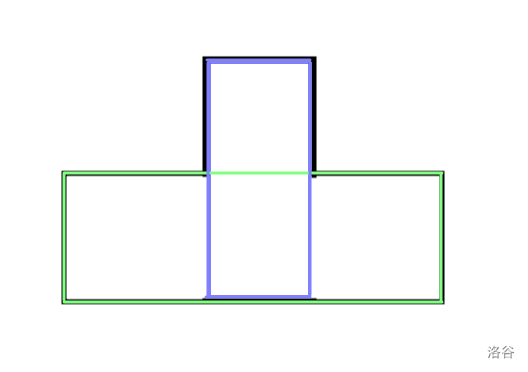
其实，按照刚才那样转移，绿色框也会考虑到。

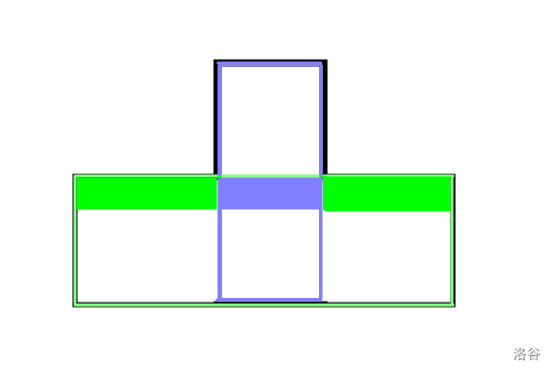
我们转移状态之前，保证 \((i, j)\) 能由 \((i- 1, j)\) 扩展过来，那么下图中填充为蓝色的部分的 \(L,R\) 表示蓝色框的宽。

而此时下图中填充为绿色的部分的 \(L,R\)，就可以表示绿色框的宽了。

仔细想一下，下图填充为绿色部分的 \(L,R\) 没有被上一行的 \(L,R\) 所影响，那么他们的 \(L,R\) 表示的即为整个绿色框的宽。在遍历 \(i,j\) 的时候，可以正常计算绿色框的大小，即绿色框被考虑到了。

代码

const int N = 2005;
int n, m, L[N][N], R[N][N], up[N][N];
bitset<N> b[N];

int main()
{
    n = read(), m = read();
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= m; ++j)
        {
            b[i][j] = read();
            L[i][j] = j, R[i][j] = j;
            up[i][j] = 1;
        }
    }

    for (int i = 1; i <= n; ++i)
        for (int j = 2; j <= m; ++j)
            if (b[i][j] != b[i][j - 1])
                L[i][j] = L[i][j - 1];

    for (int i = 1; i <= n; ++i)
        for (int j = m - 1; j >= 1; --j)
            if (b[i][j] != b[i][j + 1])
                R[i][j] = R[i][j + 1];

    int ans1 = 0, ans2 = 0;
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= m; ++j)
        {
            if (i > 1 and b[i][j] != b[i - 1][j])
            {
                up[i][j] = up[i - 1][j] + 1;
                L[i][j] = max(L[i][j], L[i - 1][j]);
                R[i][j] = min(R[i][j], R[i - 1][j]);
            }
            int len = R[i][j] - L[i][j] + 1;
            ans2 = max(ans2, len * up[i][j]);
            ans1 = max(ans1, min(len, up[i][j]) * min(len, up[i][j]));
        }
    }

    W(ans1, '\n'), W(ans2, '\n');
    return 0;
}