图的BFS与DFS

前言

本部分代码的存图方式为 \(\text{vector}\) 存图。

它与标准邻接表差别并不是很大。只是 \(\text{vector}\) 比较好写。

例题

题目链接

题目给我们一个有向图，要求我们求出从一个入度为 \(0\) 的点开始，DFS 和 BFS 的遍历顺序。

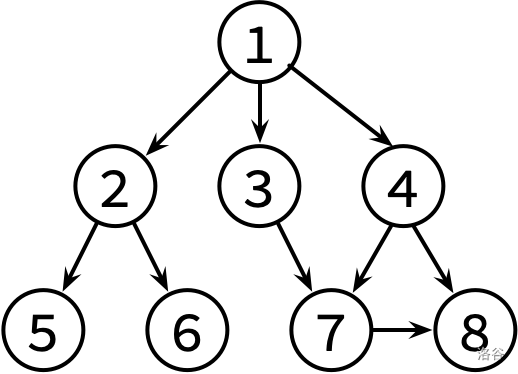
请对这个图分别进行 DFS 和 BFS，并输出遍历结果。如果有很多点可以遍历，请先遍历编号较小的那个点 (因此你可能需要先排序)。

输入样例

8 9
1 2
1 3
1 4
2 5
2 6
3 7
4 7
4 8
7 8

输出样例

1 2 5 6 3 7 8 4 
1 2 3 4 5 6 7 8 

DFS

直接感性理解，深搜即可。无任何难度。

void dfs(ll s)
{
    vis[s] = 1;
    ans.push_back(s);
    for (int i = 0; i < t[s].size(); ++i)
        if (!vis[t[s][i]])
            dfs(t[s][i]);
}

BFS

关于如何广搜，这里我就不再讲解。具体可以查看大佬博客。

这里只放代码作为参考。

void bfs(ll s)
{
    queue<ll> q;
    q.push(s);
    vis[s] = 1;
    while (!q.empty())
    {
        ll x = q.front();
        ans.push_back(x);
        q.pop();
        for (ll i = 0; i < t[x].size(); ++i)
        {
            if (!vis[t[x][i]])
            {
                q.push(t[x][i]);
                vis[t[x][i]] = 1;
            }
        }
    }
}