平时六测
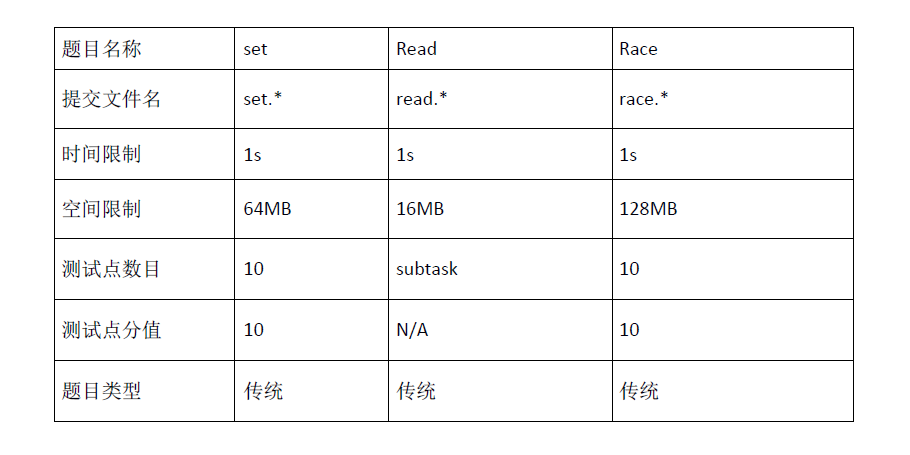
第一题：抽屉原理，维护前缀和，出现一样的中间就可以了；
我看成了不能选一样的数（其实我觉得题意有歧义，也可能是我太久没学语文了），难度翻翻，以后要认真审题；
#include<bits/stdc++.h> using namespace std; const int M = 1000005; bool dp[M]; int a[M], sum[M], ap[M]; int main(){ freopen("set.in","r",stdin); freopen("set.out","w",stdout); int n, x, ans = -1, cnt = 0; scanf("%d", &n); for(int i = 1; i <= n; i++){ scanf("%d", &a[i]); } memset(ap, -1, sizeof(ap)); ap[0] = 0; for(int i = 1; i <= n; i++){ sum[i] = (sum[i - 1] + a[i]) % n; if(ap[sum[i]] != -1) { printf("%d\n", i - ap[sum[i]]); for(int j = ap[sum[i]] + 1; j <= i; j++){ printf("%d ", j); } break; } else ap[sum[i]] = i; } }
第二题：空间问题，思路贪心，只要 max <= (n + 1) / 2就可以全部选择；
不能用数组记录种类，采用抵消思想 ;
扫的时候记录一个id， cnt;
if cnt = 0, id = a[i], cnt = 1;
else if a[i] = id, cnt++
else cnt--;
最后跑出来的id是一个理想最大值；
如果 max > (n + 1) / 2, 那么id一定是种类最多的那个数， 这个采用抵消思想易证；
如果 max < (n + 1) / 2, id不一定是个数最多的那个数，但这不影响答案；
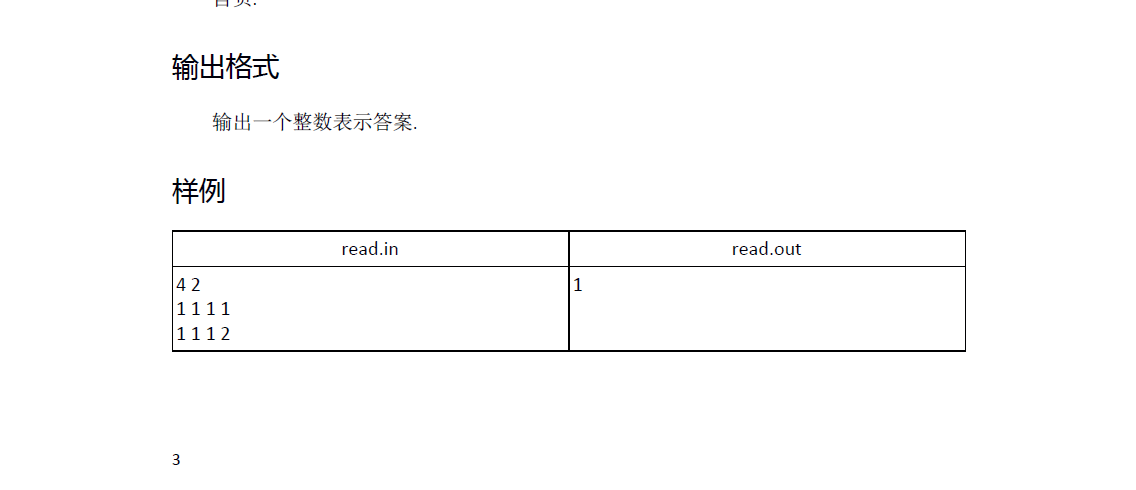
#include<bits/stdc++.h> using namespace std; #define ll long long const int M = 1005; int ct[M]; ll X[M], Y[M], Z[M]; int main(){ freopen("read.in","r",stdin); freopen("read.out","w",stdout); int N, S, M, K, ret = 0, cnt = 0; scanf("%d%d", &M, &K); for(int i = 1; i <= M; i++)scanf("%d", &ct[i]), ret += ct[i]; for(int i = 1; i <= M; i++)scanf("%lld", &X[i]); for(int i = 1; i <= M; i++)scanf("%lld", &Y[i]); for(int i = 1; i <= M; i++)scanf("%lld", &Z[i]); N = 0, S = (1 << K) - 1; ll qlst = -1; for(int i = 1; i <= M; i++){ N++; if (cnt==0) qlst = X[i] ,cnt = 1; else if (X[i] == qlst) cnt++; else cnt--; ll lst = X[i]; for(int j = 1; j < ct[i]; j++){ lst = (lst * Y[i] + Z[i]) & S; N++; if (cnt==0) qlst = lst ,cnt = 1; else if (lst == qlst) cnt++; else cnt--; } } cnt = 0; N = 0, S = (1 << K) - 1; for(int i = 1; i <= M; i++){ N++; ll lst = X[i]; if(qlst == X[i]) cnt++; for(int j = 1; j < ct[i]; j++){ lst = (lst * Y[i] + Z[i]) & S; N++; cnt += (lst == qlst); } } if(cnt > (ret + 1)/2) printf("%d\n", cnt - (ret - cnt) - 1); else puts("0"); }
第三题：Trie树， 按照每个人的得分建一棵深度为m的Trie树；
我们在Trie树上跑一个人积分的总和， 我们先按原数跑，假设现在的深度是dep，他当前排在前面，那么当 j 的这一位（dep位）改变时，这颗子树中每个排名都会整体往后降size[now]位, 而内部的相对排名是不变的；
我们记录P为当前节点中积分和 P = a1^2 + a2^2 + a3^2 +……
令S= siz[now], 那么另一个节点 P = (a1 + S) ^2 + (a2 + S)^2 + (a3 + S)^2 + ……
我们合并子树 P = P + P + (a1 + a2 + a3 + ……） * 2 * S + S*S * 2^(dep - 1) (这个节点下有（2^(dep-1)）场比赛；
用 sum = a1 + a2 + a3 + ……
所以 sum = sum * 2 + S * 2^(dep-1), P = 2 * P + 2 * S * sum + S*S * 2^(dep - 1)
#include<bits/stdc++.h> using namespace std; #define ss siz[ch[now][t^1]] #define ll long long const int M = 200005, ME = 5*1e6; const ll mod = 1e9 + 7; int a[M], tot; ll bin[M], siz[ME]; int ch[ME][2], n, m; void insert(int x){ int now = 0; for(int i = m; i >= 1; i--){ int t = bin[i-1] & x ? 1 : 0; if(!ch[now][t]) ch[now][t] = ++tot; now = ch[now][t]; siz[now]++; } } struct Node{ll sum, q;}; Node query(int x, int dep, int now){ if(!dep) return (Node) {0, 0}; int t = bin[dep - 1] & x ? 1 : 0; Node rs = query(x, dep - 1, ch[now][t]); ll sum = (rs.sum * 2 % mod + ss * bin[dep - 1] % mod) % mod; ll q = (rs.q * 2 % mod + 2 * rs.sum * ss % mod + ss * ss % mod * bin[dep - 1] % mod ) % mod; return (Node) {sum, q}; } int main(){ freopen("race.in","r",stdin); freopen("race.out","w",stdout); scanf("%d%d", &n, &m); bin[0] = 1; for(int i = 1; i <= 31; i++) bin[i] = (bin[i - 1] << 1) % mod; for(int i = 1; i <= n; i++){ scanf("%d", &a[i]); insert(a[i]); } ll ans = 0; for(int i = 1; i <= n; i++){ Node p = query(a[i], m, 0); //printf("%lld %lld\n", p.sum, p.q); ans = ans ^ p.q; } printf("%lld\n", ans); }
