裸地并查集

【例4-7】亲戚(relation)

链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1346
时间限制: 1000 ms 内存限制: 65536 KB

【题目描述】

或许你并不知道，你的某个朋友是你的亲戚。他可能是你的曾祖父的外公的女婿的外甥女的表姐的孙子。如果能得到完整的家谱，判断两个人是否是亲戚应该是可行的，但如果两个人的最近公共祖先与他们相隔好几代，使得家谱十分庞大，那么检验亲戚关系实非人力所能及。在这种情况下，最好的帮手就是计算机。为了将问题简化，你将得到一些亲戚关系的信息，如Marry和Tom是亲戚，Tom和Ben是亲戚，等等。从这些信息中，你可以推出Marry和Ben是亲戚。请写一个程序，对于我们的关于亲戚关系的提问，以最快的速度给出答案。

【输入】

输入由两部分组成。

第一部分以N，M开始。N为问题涉及的人的个数(1≤N≤20000)。这些人的编号为1,2,3,…, N。下面有M行(1≤M≤1000000)，每行有两个数 $a_{i}, b_{i}$

第二部分以Q开始。以下Q行有Q个询问(1≤ Q ≤1000000)，每行为 $c_{i}, d_{i}$

【输出】

对于每个询问 $c_{i}, d_{i}$

【输入样例】

【输出样例】

Yes
No
Yes

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn = 20005;
int father[maxn];
int find(int x)
{
    return father[x]==x?x:father[x]=find(father[x]);
}
bool check(int a,int b)
{
    if(a==b)return 1;
    else return find(a)==find(b);    
}
void unio(int a,int b)
{
    int c=find(a),d=find(b);
    if(c!=d)father[c]=d;
}
int main()
{
    int N,M,Q;
    cin>>N>>M;
    for(int i=1;i<=N;i++)
        father[i]=i;
    for(int i=1;i<=M;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        if(a!=b)unio(a,b);
    }
    cin>>Q;
    for(int i=1;i<=Q;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        if(check(a,b))printf("Yes\n");
        else printf("No\n");
    }
}

团伙(group)

时间限制: 1000 ms 内存限制: 65536 KB

【题目描述】

在某城市里住着n个人，任何两个认识的人不是朋友就是敌人，而且满足：

1、我朋友的朋友是我的朋友；

2、我敌人的敌人是我的朋友；

所有是朋友的人组成一个团伙。告诉你关于这n个人的m条信息，即某两个人是朋友，或者某两个人是敌人，请你编写一个程序，计算出这个城市最多可能有多少个团伙？

【输入】

第1行为n和m，1<n<1000,1≤m≤100 000；

以下m行，每行为p x y，p的值为0或1，p为0时，表示x和y是朋友，p为1时，表示x和y是敌人。

【输出】

一个整数，表示这n个人最多可能有几个团伙。

【输入样例】

【输出样例】

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1005;
int f[maxn],e[maxn];
bool vis[maxn];
int find(int x){
    return f[x] == x ? x : f[x] = find(f[x]);
}
void Union(int u,int v){
    int f1 = find(u), f2 = find(v);
    if(f1 != f2)f[f1] = f2;
}
void Sep(int u,int v){
    Union(e[u], v);
}
int main(){
    int N,M,cnt = 0;
    cin>>N>>M;
    for(int i = 1; i <= N; i++)
        f[i] = i;
    for(int i = 1; i <= M; i++){
        int u, v, p;
        cin>>p>>u>>v;
        if(!p)Union(u, v);
        if(p){
            if(!e[u])e[u] = v;
            else Sep(u, v);
            if(!e[v])e[v] = u;
            else Sep(v, u);
        }        
    }
    for(int i = 1; i <= N; i++)
        if(!vis[find(i)])vis[find(i)] = 1, cnt++;
    cout<<cnt;
}

搭配购买(buy)

时间限制: 1000 ms 内存限制: 65536 KB

【题目描述】

Joe觉得云朵很美，决定去山上的商店买一些云朵。商店里有n朵云，云朵被编号为1，2，…...，n，并且每朵云都有一个价值。但是商店老板跟他说，一些云朵要搭配来买才好，所以买一朵云则与这朵云有搭配的云都要买。

但是Joe的钱有限，所以他希望买的价值越多越好。

【输入】

第1行n，m，w，表示n朵云，m个搭配，Joe有w的钱。

第2~n+1行，每行ci，di表示i朵云的价钱和价值。

第n+2~n+1+m行，每行ui，vi，表示买ui就必须买vi，同理，如果买vi就必须买ui。

【输出】

一行，表示可以获得的最大价值。

【输入样例】

【输出样例】

【提示】

【数据范围】

30%的数据保证：n≤100

50%的数据保证：n≤1,000；m≤100；w≤1,000

100%的数据保证：n≤10,000；0≤m≤5000；w≤10,000

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 10005;
int f[maxn],c[maxn],d[maxn],C[maxn],D[maxn],p[maxn];

int find (int x)
{
    return f[x]==x?x:f[x]=find(f[x]);
}
void unin(int a,int b)
{
    int c=find(a),d=find(b);
    if(c==d)return ;
    f[c]=d;
}

int main()
{
    int N,M,W;
    cin>>N>>M>>W;
    for(int i=1;i<=N;i++)f[i]=i;
    for(int i=1;i<=N;i++)
        scanf("%d%d",&c[i],&d[i]);
    for(int i=1;i<=M;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        unin(a,b);
    }
    for(int i=1;i<=N;i++)
    {
        int u=find(i);
        C[u]+=c[i];
        D[u]+=d[i];
    }
    for(int i=1;i<=N;i++)
    {
        if(!C[i]||!D[i])continue;
        for    (int j=W;j>=C[i];j--)
        {
            p[j]=max(p[j],p[j-C[i]]+D[i]);
        }
    }
    cout<<p[W]<<endl;
    return 0;    
}

家谱(gen)

时间限制: 1000 ms 内存限制: 65536 KB

【题目描述】

现代的人对于本家族血统越来越感兴趣，现在给出充足的父子关系，请你编写程序找到某个人的最早的祖先。

【输入】

由多行组成，首先是一系列有关父子关系的描述，其中每一组父子关系由二行组成，用#name的形式描写一组父子关系中的父亲的名字，用+name的形式描写一组父子关系中的儿子的名字；接下来用?name的形式表示要求该人的最早的祖先；最后用单独的一个$表示文件结束。规定每个人的名字都有且只有6个字符，而且首字母大写，且没有任意两个人的名字相同。最多可能有1000组父子关系，总人数最多可能达到50000人，家谱中的记载不超过30代。

【输出】

按照输入的要求顺序，求出每一个要找祖先的人的祖先，格式：本人的名字+一个空格+祖先的名字+回车。

【输入样例】

#George
+Rodney
#Arthur
+Gareth
+Walter
#Gareth
+Edward
?Edward
?Walter
?Rodney
?Arthur
$

【输出样例】

Edward Arthur
Walter Arthur
Rodney George
Arthur Arthur
注意：没有找到父亲map返回的是“”，s.substr是截取字串函数

#include<cstdio>
#include<cstring>
#include<map>
using namespace std;
const int maxn = 100005;
map <string,string>father;
string find(string x)
{
    return father[x]==x?x:father[x]=find(father[x]);
}
int main()
{
    ios::sync_with_stdio(false);
    string f;
    while(1)
    {
        string s;
        cin>>s;
        if(s=="$")break;
        if(s[0]=='#')
        {
            f=s.substr(1,s.size()-1);
            if(find(f)=="")father[f]=f;
            else f=father[f];
            //cout<<"@"<<father[f]<<endl;
        }
        if(s[0]=='+')
        {
            string son;
            son=s.substr(1,s.size()-1);
            father[son]=find(f);
            //cout<<"!"<<father[son]<<endl;
        }
        if(s[0]=='?')
        {
            string st=s.substr(1,s.size()-1);
            cout<<st<<" "<<find(st)<<endl;
        }
    }
    
}

亲戚

时间限制: 1000 ms 内存限制: 65536 KB

【题目描述】

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的某个人所在家族的人数。

规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。

【输入】

第一行：三个整数n，（n≤100,000,m≤200,000），分别表示有n个人，m个信息。

以下m行：信息包含两种形式：

M a b：表示a和b具有亲戚关系。

Q a：要求输出a所在家族的人数。

【输出】

要求输出a所在家族的人数。

【输入样例】

【输出样例】

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn = 100005;
int father[maxn],num[maxn];
int find(int x)
{
    return father[x]==x?x:father[x]=find(father[x]);
}
int check(int a)
{
    return num[find(a)];    
}
void unio(int a,int b)
{
    int c=find(a),d=find(b);
    if(c!=d)
    {
        num[d]+=num[c];
        father[c]=d;
    }
}
int main()
{
    int N,M,Q;
    cin>>N>>M;
    for(int i=1;i<=N;i++)
        {
            father[i]=i;
            num[i]=1;
        }            

    for(int i=1;i<=M;i++)
    {
        string order;                
        cin>>order;
        //cout<<order<<endl;
        //cout<<"a";
        if(order=="M")
        {
            int a,b;
            scanf("%d%d",&a,&b);
            if(a!=b)unio(a,b);
        }
        else if(order=="Q")
        {
            int a;
            scanf("%d",&a);
            printf("%d\n",(check(a)));
        }
    }
    
}

【例4-8】格子游戏

时间限制: 1000 ms 内存限制: 65536 KB

【题目描述】

Alice和Bob玩了一个古老的游戏：首先画一个n × n的点阵（下图n = 3）

接着，他们两个轮流在相邻的点之间画上红边和蓝边：

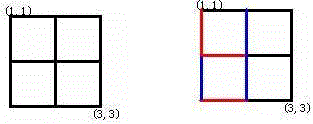
直到围成一个封闭的圈（面积不必为1）为止，“封圈”的那个人就是赢家。因为棋盘实在是太大了(n ≤ 200)，他们的游戏实在是太长了！他们甚至在游戏中都不知道谁赢得了游戏。于是请你写一个程序，帮助他们计算他们是否结束了游戏？

【输入】

输入数据第一行为两个整数n和m。m表示一共画了m条线。以后m行，每行首先有两个数字(x, y)，代表了画线的起点坐标，接着用空格隔开一个字符，假如字符是"D "，则是向下连一条边，如果是"R "就是向右连一条边。输入数据不会有重复的边且保证正确。

【输出】

输出一行：在第几步的时候结束。假如m步之后也没有结束，则输出一行“draw”。

【输入样例】

【输出样例】

题解：二维并查集，当两个点在同一集合中，则它们已首尾相连

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn = 301;
struct node{
    int x,y;
}f[maxn][maxn];
node find(node a)
{
    if((f[a.x][a.y].x==a.x)&&(f[a.x][a.y].y==a.y))
        return f[a.x][a.y];
    return f[a.x][a.y]=find(f[a.x][a.y]);
}
int main()
{
    int N,M;
    cin>>N>>M;
    for(int i=1;i<=N;i++)
        for(int j=1;j<=N;j++)
            f[i][j].x=i,f[i][j].y=j;
    for(int i=1;i<=M;i++)
    {
        int x,y;
        char c;
        node k1,k2;
        cin>>x>>y>>c;
        if(c=='D')
            k1=find(f[x][y]),k2=find(f[x+1][y]);
        else 
            k1=find(f[x][y]),k2=find(f[x][y+1]);
        if((k1.x==k2.x)&&(k1.y==k2.y)){
            cout<<i<<endl;return 0;
　　　　　}
        f[k1.x][k1.y]=k2;
        
    }
    cout<<"draw"<<endl;
}

posted @ 2018-02-25 18:55 Ed_Sheeran 阅读(303) 评论(0) 编辑收藏举报

刷新页面返回顶部

Ed_Sheeran

裸地并查集

【例4-7】亲戚(relation)

【题目描述】

【输入】

【输出】

【输入样例】

【输出样例】

团伙(group)

【题目描述】

【输入】

【输出】

【输入样例】

【输出样例】

搭配购买(buy)

【题目描述】

【输入】

【输出】

【输入样例】

【输出样例】

【提示】

家谱(gen)

【题目描述】

【输入】

【输出】

【输入样例】

【输出样例】

亲戚

【题目描述】

【输入】

【输出】

【输入样例】

【输出样例】

【例4-8】格子游戏

【题目描述】

【输入】

【输出】

【输入样例】

【输出样例】

公告