CG——Grab Cut
https://blog.csdn.net/zouxy09/article/details/8534954 (本文部分摘自此博客,共3篇,都是很好的学习资料)
grab cut是在graph cut上发展来的,作用就像PS中的魔棒。先选中可能的前景TU,剩余则是背景TB, 通过迭代使TU中可能的前景变成绝对的前景,这个筛选过程可以用最小割实现。
整个流程:

前提:
1、颜色模型
对于Gibbs能量的理解:https://blog.csdn.net/zouxy09/article/details/8532111 (这部分是graph cut的理解,是grab cut的前提)
我们采用RGB颜色空间,分别用一个K个高斯分量(一取般K=5)的全协方差GMM(混合高斯模型)来对目标和背景进行建模。于是就存在一个额外的向量k = {k1, . . ., kn, . . ., kN},其中kn就是第n个像素对应于哪个高斯分量,kn∈ {1, . . . K}。对于每个像素,要不来自于目标GMM的某个高斯分量,要不就来自于背景GMM的某个高斯分量。
所以用于整个图像的Gibbs能量为(式7):
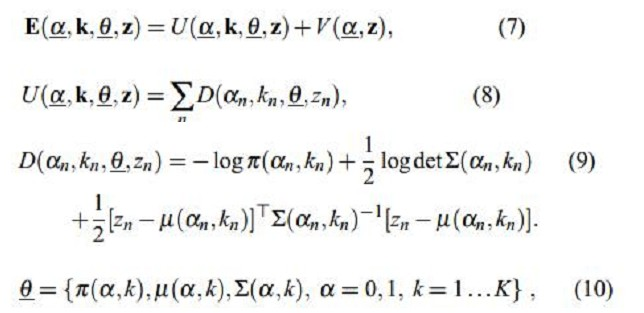
其中,U就是区域项,和上一文说的一样,你表示一个像素被归类为目标或者背景的惩罚,也就是某个像素属于目标或者背景的概率的负对数。
我们知道混合高斯密度模型是如下形式:
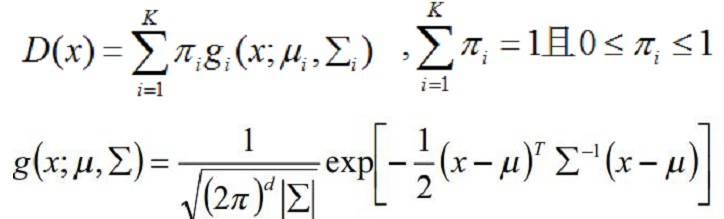
所以取负对数之后就变成式(9)那样的形式了,其中GMM的参数θ就有三个:每一个高斯分量的权重π、每个高斯分量的均值向量u(因为有RGB三个通道,故为三个元素向量)和协方差矩阵∑(因为有RGB三个通道,故为3x3矩阵)。如式(10)。也就是说描述目标的GMM和描述背景的GMM的这三个参数都需要学习确定。一旦确定了这三个参数,那么我们知道一个像素的RGB颜色值之后,就可以代入目标的GMM和背景的GMM,就可以得到该像素分别属于目标和背景的概率了,也就是Gibbs能量的区域能量项就可以确定了,即图的t-link的权值我们就可以求出。那么n-link的权值怎么求呢?也就是边界能量项V怎么求?
![]()
其中m,n表示相邻的点(8个方向)
解读:
Initialisation:
(1)用户通过直接框选目标来得到一个初始的trimap T,即方框外的像素全部作为背景像素TB,而方框内TU的像素全部作为“可能是目标”的像素。
(2)对TB内的每一像素n,初始化像素n的标签αn=0,即为背景像素;而对TU内的每个像素n,初始化像素n的标签αn=1,即作为“可能是目标”的像素。
(3)经过上面两个步骤,我们就可以分别得到属于目标(αn=1)的一些像素,剩下的为属于背景(αn=0)的像素,这时候,我们就可以通过这个像素来估计目标和背景的GMM了。我们可以通过k-mean算法分别把属于目标和背景的像素聚类为K(K=5)类,即GMM中的K个高斯模型,这时候GMM中每个高斯模型就具有了一些像素样本集,这时候它的参数均值和协方差就可以通过他们的RGB值估计得到,而该高斯分量的权值可以通过属于该高斯分量的像素个数与总的像素个数的比值来确定。
关于kmeans(所谓的距离换成像素差,再把一维的拓展到三维):

Iterative minimisation:
(1)对每个像素分配GMM中的高斯分量(例如像素n是目标像素,那么把像素n的RGB值代入目标GMM中的每一个高斯分量中,概率最大的那个就是最有可能生成n的,也即像素n的第kn个高斯分量):
![]() argmin: 使D取最小值的k.
argmin: 使D取最小值的k.
(2)对于给定的图像数据Z,学习优化GMM的参数(因为在步骤(1)中我们已经为每个像素归为哪个高斯分量做了归类,那么每个高斯模型就具有了一些像素样本集,这时候它的参数均值和协方差就可以通过这些像素样本的RGB值估计得到,而该高斯分量的权值可以通过属于该高斯分量的像素个数与总的像素个数的比值来确定。):
![]() θ的本质就是一堆参数
θ的本质就是一堆参数
(3)分割估计(通过1中分析的Gibbs能量项,建立一个图,并求出权值t-link和n-link,然后通过max flow/min cut算法来进行分割(这个算法我是直接去网上下的包),邻接点就V作为权值,和sink&tank的权值用U:
![]()
(4)重复步骤(1)到(3),直到收敛。经过(3)的分割后,每个像素属于目标GMM还是背景GMM就变了,所以每个像素的kn就变了,故GMM也变了,所以每次的迭代会交互地优化GMM模型和分割结果。另外,因为步骤(1)到(3)的过程都是能量递减的过程,所以可以保证迭代过程会收敛。
(5)采用border matting对分割的边界进行平滑等等后期处理。(本人没有处理)
一些注意:
1.开始我为α=0,1的分别造了一个结构体跑全程,后来发现跑网络流又要合并,只能重。最终借鉴jdr大佬的封装(本人第一次自己写代码封装),GMM,Kmeans,三元组都可以封装
2.Kmeans要注意有可能一组里一个都没分到的情况;GMM要注意分母不为0(多处坑,死了好多次,除0会报错nan)
3.由于有些色块在结果中会连一起,效仿jdr加了连通块优化
4.网络流建边注意序号关系
5.计算D最好用(9),不要直接带GMM的pdf
……
主要过程:

// #pragma GCC optimize(3) #include<queue> #include<cstdio> #include<iostream> #define mfor(i, b, c) for(int i = (b); i < (c); i++) #include "mylinalg.hpp" #include "myguass.hpp" #include "mykmeans.hpp" #include "flow/graph.hpp" #include "flow/Cut.hpp" using namespace std; const int MAXN = 1000000; double beta, lamda=3; //gama??? int image_n, image_m, left_up_x, left_up_y, right_down_x, right_down_y; int totcode; triple pixel_z[MAXN]; int label_k[MAXN], label_alpha[MAXN], pixel_code[2101][2101];//!!! GMM_model G[2]; int di[8]={0,-1,-1,-1,0,1,1,1}; int dj[8]={-1,-1,0,1,1,1,0,-1}; void Readimage(); void Initialization(); void Iterative_minimisation(); void Biggest(); void Writeimage(); void debug1(){ freopen("debug1.out","w",stdout); mfor(i, 0, image_n) mfor(j, 0, image_m) printf("%d ",label_k[pixel_code[i][j]]); } int main(){ Readimage(); printf("read done\n"); Initialization(); printf("init done\n"); Iterative_minimisation(); printf("cutting done\n"); Biggest(); // printf("Biggest done\n"); Writeimage(); // printf("writing done\n"); return 0; } void Writeimage(){ freopen("data.out","w",stdout); int tt=0; mfor(i, 0, image_n) mfor(j, 0, image_m){ // tt++; mfor(t, 0, 3) printf("%d ", int(0.1+pixel_z[pixel_code[i][j]][t] * label_alpha[pixel_code[i][j]])); puts(""); } // cout<<tt<<endl;/ } void Readimage(){ freopen("data.in","r",stdin); scanf("%d%d%d%d%d%d",&image_n,&image_m,&left_up_y,&left_up_x,&right_down_y,&right_down_x); printf("%d %d\n", image_n, image_m); mfor(i, 0, image_n) mfor(j, 0, image_m){ int a,b,c; scanf("%d%d%d",&a,&b,&c); pixel_code[i][j] = ++totcode; pixel_z[totcode] = triple(a, b, c); if(i>left_up_y && i <right_down_y && j>left_up_x && j<right_down_x) label_alpha[totcode] = 1; } } void Build_GMM(bool fg = 0){ G[0].init(); G[1].init(); mfor(i, 0, totcode) G[label_alpha[i]].component[label_k[i]].cal_1(pixel_z[i]); G[0].Process(); G[1].Process(); mfor(i, 0, totcode){ G[label_alpha[i]].component[label_k[i]].cal_2(pixel_z[i]); } G[0].Done(); G[1].Done(); } void Build_graph(CutGraph& _graph){ // freopen("mybuildg.out","w",stdout); int vcnt = image_n*image_m, ecnt = 2*(4*image_m*image_n - 3*(image_n+image_m) + 2); _graph = CutGraph(vcnt, ecnt); int bt=0; mfor(i, 0, image_n) mfor(j, 0, image_m){ bt++; int now = pixel_code[i][j]; triple pixz = pixel_z[now]; int vnum = _graph.addVertex(); double Sw = 0, Tw = 0; if(label_alpha[now]){ Sw = G[0].getD(pixz); Tw = G[1].getD(pixz); } else Sw = 10000; //break with T, inf with S(belong to S) // if(Tw) // printf("%d %d %lf %lf\n", i, j, Sw, Tw); _graph.addVertexWeights(vnum, Sw, Tw); //V(α, z) = γ * dis(m,n)^(−1) [αn != αm] exp(−β(zm −zn))^2 double val = 0; if(i){ val = lamda * exp(-beta*square(pixz - pixel_z[pixel_code[i-1][j]])); _graph.addEdges(vnum, vnum - image_m, val); } if(j){ val = lamda * exp(-beta*square(pixz - pixel_z[pixel_code[i][j-1]])); _graph.addEdges(vnum, vnum - 1, val); } if(i&&j){ val = lamda/1.4142135 * exp(-beta*square(pixz - pixel_z[pixel_code[i-1][j-1]])); _graph.addEdges(vnum, vnum - image_m - 1, val); } if(i&&j<image_m-1){ val = lamda/1.4142135 * exp(-beta*square(pixz - pixel_z[pixel_code[i-1][j+1]])); _graph.addEdges(vnum, vnum - image_m + 1, val); } } } void Minimization(CutGraph& _graph){ Build_graph(_graph); printf("build graph done\n"); _graph.maxFlow(); printf("maxflow done\n"); } bool change_alpha(CutGraph& _graph){ bool ans=false; // freopen("debugchangealpha.out","w",stdout); mfor(i, left_up_y, right_down_y) mfor(j, left_up_x, right_down_x){ // printf("%d %d %d %d\n",i, j, _graph.isSourceSegment(pixel_code[i][j]-1), label_alpha[pixel_code[i][j]]); } mfor(i, left_up_y, right_down_y) mfor(j, left_up_x, right_down_x){ if(!_graph.isSourceSegment(pixel_code[i][j]-1) && label_alpha[pixel_code[i][j]]){ label_alpha[pixel_code[i][j]] = 0; ans = true; } } return ans; } void Iterative_minimisation(){ int cnt = 0; while(true){ cnt++; printf("This is %d GMM\n", cnt); // debug2(); mfor(i, 0, totcode) if(label_alpha[i]) label_k[i] = G[1].argminD(pixel_z[i]); Build_GMM(1); CutGraph graph; Minimization(graph); printf("minimization done\n"); if(!change_alpha(graph)){ // cout<<"nochange"<<endl; return; break; } printf("this is %d times!!!!\n",cnt); if(cnt == 20)break; } } void Initialization(){ // beta(alpha != ???) mfor(i, 0, image_n) mfor(j, 0, image_m) mfor(t, 0, 4){ int newi = i + di[t], newj = j + dj[t]; if(newi < 0 || newj < 0 || newi == image_n || newj == image_m) continue; int newpos = pixel_code[newi][newj]; beta += square(pixel_z[pixel_code[i][j]] - pixel_z[newpos]); } beta = 1.0/(2*beta/(4*image_n*image_m - 3*image_n - 3*image_m +2)); KMEANS(0, label_k, label_alpha, pixel_z, totcode); KMEANS(1, label_k, label_alpha, pixel_z, totcode); Build_GMM(); } void Biggest(void){ int* bel = new int[image_m*image_n]; int* count = new int[10000]; int cnt=1; mfor(i, 0, image_n) mfor(j, 0, image_m){ if(label_alpha[pixel_code[i][j]]){ bel[pixel_code[i][j]]=0; } } mfor(i, 0, image_n) mfor(j, 0, image_m){ if(label_alpha[pixel_code[i][j]]){ if(!bel[pixel_code[i][j]]){ bel[pixel_code[i][j]]=++cnt; count[cnt]=1; std::queue<int>rQ; std::queue<int>cQ; while(!rQ.empty())rQ.pop(); while(!cQ.empty())cQ.pop(); rQ.push(i);cQ.push(j); while(!rQ.empty()){ int nowi = rQ.front();rQ.pop(); int nowj = cQ.front();cQ.pop(); for(int d=0;d<8;++d){ int nxti = nowi + di[d]; int nxtj = nowj + dj[d]; int nxtc = pixel_code[nxti][nxtj]; if(label_alpha[nxtc]&&(!bel[nxtc])){ bel[nxtc] = cnt; count[cnt]++; rQ.push(nxti); cQ.push(nxtj); } } } } } } int maxt=1; for(int i=2;i<=cnt;++i) if(count[maxt]<count[i]) maxt=i; mfor(i, 0, image_n) mfor(j, 0, image_m){ if(label_alpha[pixel_code[i][j]]&&bel[pixel_code[i][j]]!=maxt){ bool fg=0; for(int d=0;d<8;++d){ int nxti = i + di[d]; int nxtj = j + dj[d]; int nxtc = pixel_code[nxti][nxtj]; if(bel[nxtc]==maxt){fg=1;} } if(!fg) label_alpha[pixel_code[i][j]]=0; } } delete [] count; delete [] bel; return ; }
kmeans处理:

#include<stdlib.h> #include<ctime> using namespace std; double getrandnumber(int lower, int upper){ return lower + (upper - lower) * (rand()%10001) / (10000.0); } triple miu[5], low, up; int num[5]; void KMEANS(int opt, int *gpk, int *alpha, triple *pixel_z, int tot){ srand(time(NULL)); low[0] = low[1] = low[2] = inf; mfor(i, 0, tot) if(opt == alpha[i]){ mfor(t, 0, 3) low[t] = min(low[t], pixel_z[i][t]), up[t] = max(up[t], pixel_z[i][t]); } mfor(k, 0, 5) mfor(t, 0, 3) miu[k][t] = getrandnumber(low[t], up[t]); double newJ = inf, oldJ = inf; int tt=0; do{ tt++; oldJ = newJ; newJ = 0; mfor(k, 0, 5)num[k] = 0; // asign k mfor(i, 0, tot) if(opt == alpha[i]){ int ret = 0; mfor(k, 1, 5){ if(square(pixel_z[i] - miu[k]) < square(pixel_z[i] - miu[ret])) ret = k; } gpk[i] = ret; num[ret]++; } mfor(k, 0, 5) miu[k] = triple(0); mfor(i, 0, tot) miu[gpk[i]] = miu[gpk[i]] + pixel_z[i]; // for empty cluster mfor(k, 0, 5) if(!num[k]){ int ret = 0; mfor(t, 1, 5) if(num[t] > num[ret]) ret = t; int now = 0; double maxdis = -inf; mfor(i, 0, tot) if(opt == alpha[i] && gpk[i] == ret){ double dis = square(pixel_z[i] - (miu[ret]/num[ret])); if(dis > maxdis) maxdis = dis, now = i; } num[ret]--; num[k]++; miu[ret] = miu[ret] - pixel_z[now]; miu[k] = miu[k] + pixel_z[now]; gpk[now] = k; } //renew miu mfor(k, 0, 5) miu[k] = miu[k] / num[k]; mfor(i, 0, tot) newJ += square(pixel_z[i] - miu[gpk[i]]); printf("iterate %d\n",tt); }while(oldJ - newJ > 1e-3); }
三元组和矩阵计算:

#include<cmath> #include<cstring> #include<algorithm> const double eps = 1e-10; // #define mfor(i, b, c) for(int i = b; i < c; i++) struct triple { /* data */ double mat[3]; triple(){ } triple(double x){ mfor(i, 0, 3) mat[i] = x; } triple(double a, double b, double c){ mat[0]=a;mat[1]=b;mat[2]=c; } double& operator [] (int idx){return mat[idx];} triple friend operator + (triple A, triple B){ triple ans; mfor(i, 0, 3) ans[i] = A[i] + B[i]; return ans; } triple friend operator - (triple A, triple B){ triple ans; mfor(i, 0, 3) ans[i] = A[i] - B[i]; return ans; } double friend operator * (triple A, triple B){ double ans = 0; mfor(i, 0, 3) ans += A[i] * B[i]; return ans; } triple friend operator * (triple A, double k){ triple ans; mfor(i, 0, 3) ans[i] = A[i] * k; return ans; } triple friend operator / (triple A, int k){ triple ans; mfor(i, 0, 3) ans[i] = A[i] / k; return ans; } }; double square(triple A){return A * A;} struct Matrix { double v[3][3]; Matrix(){} Matrix(bool t){ memset(v, 0, sizeof(v)); if(t) mfor(i, 0, 3) mfor(j, 0, 3) v[i][j] = (i == j); } Matrix(triple x, bool form){ memset(v, 0, sizeof(v)); if(form) mfor(i, 0, 3) v[0][i] = x[i]; // x x x // 0 0 0 // 0 0 0 else mfor(i, 0, 3) v[i][0] = x[i]; // x 0 0 // x 0 0 // x 0 0 } double* operator [] (int idx){return v[idx];} Matrix friend operator *(Matrix A, Matrix B){ Matrix ans; ans = Matrix(0); mfor(i, 0, 3) mfor(j, 0, 3) mfor(k, 0, 3) ans[i][j] += A[i][k] * B[k][j]; return ans; } Matrix friend operator +(Matrix A, Matrix B){ Matrix ans; mfor(i, 0, 3) mfor(j, 0, 3) ans[i][j] = A[i][j] + B[i][j]; return ans; } bool friend operator ==(Matrix A, Matrix B){ mfor(i, 0, 3) mfor(j, 0, 3) if(A[i][j] != B[i][j]) return 0; return 1; } Matrix friend operator *(Matrix A, double k){ Matrix ans; mfor(i, 0, 3) mfor(j, 0, 3) ans[i][j] = A[i][j] * k; return ans; } Matrix friend operator /(Matrix A, double k){ Matrix ans; mfor(i, 0, 3) mfor(j, 0, 3) ans[i][j] = A[i][j] / k; return ans; } }; double det(Matrix M){ return M[0][0]*(M[1][1]*M[2][2]-M[2][1]*M[1][2]) + M[0][1]*(M[1][2]*M[2][0]-M[2][2]*M[1][0]) + M[0][2]*(M[1][0]*M[2][1]-M[1][1]*M[2][0]); } Matrix inv(Matrix M){ Matrix Inv; for(int i=0;i<3;i++) for(int j=0;j<3;j++) Inv[j][i]=M[(i+1)%3][(j+1)%3] * M[(i+2)%3][(j+2)%3] -M[(i+2)%3][(j+1)%3] * M[(i+1)%3][(j+2)%3]; return Inv / det(M); } double Trace(Matrix M){return M[0][0]+M[1][1]+M[2][2];}
GMM:

// #define mfor(i, b, c) for(int i = b; i < c; i++) const double PI = acos(-1.0); const double inf = 1e18; ////??????????????????????? struct Guassion { /* data */ triple miu; Matrix sigma; int Mass; double pdf(triple x){ Matrix A = Matrix(x-miu, 1); Matrix B = inv(sigma); Matrix C = Matrix(x-miu,0); Matrix D = A * B; Matrix tmp = D * C; // Matrix tmp = Matrix(x-miu, 1)*inv(sigma)*Matrix(x-miu, 0); double ans = 1.0/(pow(2*PI, 1.5)*sqrt(det(sigma)))*exp(tmp[0][0]*(-0.5)); return ans; } void init(){ miu = triple(0); sigma = Matrix(0); Mass = 0; } void cal_1(triple x){ miu = miu + x; Mass += 1; } void cal_2(triple x){ sigma = sigma + Matrix(x - miu, 0) * Matrix(x - miu, 1); // 巧用矩阵乘法 } void ep(){ mfor(i, 0, 3) mfor(j, 0, 3) if(sigma[i][j] < 1e-7) sigma[i][j] = 1e-7; } }; struct GMM_model { Guassion component[5]; double weight[5]; int totMass; void init(){//checked mfor(i, 0, 5){ component[i].init(); weight[i] = 0; } totMass = 0; } void Process(){//checked mfor(i, 0, 5)totMass += component[i].Mass; mfor(i, 0, 5){ weight[i] = component[i].Mass * 1.0 / totMass; if(component[i].Mass > 0) component[i].miu = component[i].miu / component[i].Mass; } } void Done(){//checked mfor(i, 0, 5) component[i].ep(); mfor(i, 0, 5) if(component[i].Mass > 1) component[i].sigma = component[i].sigma / (1.0*component[i].Mass - 1); } double getD(triple pt){ int k = argminD(pt); double ans=-log(weight[k]) + 0.5*log(det(component[k].sigma)) +0.5*(Matrix(pt - component[k].miu,1)*inv(component[k].sigma)*Matrix(pt - component[k].miu,0))[0][0]; return ans; } int argminD(triple pt){//checked int ret = 0; double ans = 0; mfor(t, 0, 5){ double newpro = weight[t] * component[t].pdf(pt); if(newpro > ans) ans = newpro, ret = t; } return ret; } };
网络流是网上找的包
成果:






总结:这次比泊松的代码实现更难,对数学要求也很高,但理清流程后还是可以实现。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号