皮亚诺曲线距离 2020 蓝桥杯国赛
皮亚诺曲线距离 2020 蓝桥杯国赛
链接:
题目:https://www.lanqiao.cn/courses/2786/learning/?id=131138
提交平台:https://www.lanqiao.cn/problems/1023/learning/
题目大意:


题解:
算法:递归
求 \((x_1,y_1)\) 和 \((x_2,y_2)\) 之间的距离,那么求 \((0,0)\) 到 \((x_1,y_1)\) 和 \((0,0)\) 到 \((x_2,y_2)\) ,然后做差即可。
求 \((0,0)\) 到 \((x,y)\) ,可以一阶一阶的算。
-
对于 k 阶,那么它就有 9 个位置。
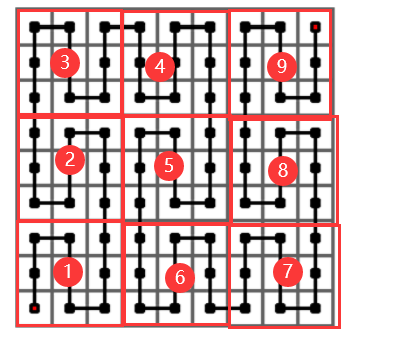
-
然后我们对每一个位置进行分类讨论,注意 \(x,y\) 都从 0 开始计算
-
假设此时是第 \(k\) 阶,那么边长就是 \(len = 3^k\) ,如果从起点走到终点距离是 :\(cnt = 3^{2*k}/9\)
-
如果 \(x<len/3\)
- 如果\(y<len/3\) 说明在第一个部分,且起点位置不变,所以继续递归
- else 如果 \(y<len/3*2\) 说明在第二个部分,起点位置改变,所以 x 要进行变化,因为此时起点就变成了 \((len/3-1,len/3)\) ,所以 \((x,y)\) -> \((len/3-1-x,y-len/3)\) ,需要加上 1 这个部分的距离,也就是 \(cnt\)
- else 就说明在第 3 部分,起点位置改变:\((0,len/3*2)\) ,所以 \((x,y)\) -> \((x,y - len/3*2)\) ,需要加上 1 2 部分的距离,也就是 \(cnt*2\)
-
else 如果 \(x<len*2/3\)
- 如果 \(y<len/3\) 说明在第 6 部分,起点变成:\((len/3,len/3-1)\) ,\((x,y)\) 变成:\((x - len/3,len/3-1-y)\) ,加上 1 2 3 4 5 部分,也就是 \(cnt*5\)
- else 如果 \(y<len*2/3\) ,说明在第 5 部分,起点变成:\((len*2/3-1,len*2/3-1)\) ,\((x,y)\) 变成:\((len*2/3-1-x,len*2/3-1-y)\) ,加上 1 2 3 4 部分,也就是 \(cnt*4\)
- else 说明在第 4 部分,起点变成:\((len/3,len-1)\) ,\((x,y)\) 变成:\((x - len /3,len-1-y)\) ,加上 1 2 3 部分,也就是 \(cnt*3\)
-
\(x<len\)
- 如果 \(y<len/3\) 说明在第 7 部分,起点变成 :\((len*2/3,0)\) ,\((x,y)\) 变成 :\((x - len*2/3,y)\) ,加上 1 2 3 4 5 6 部分,也就是 \(cnt*6\)
- 如果 \(y<len*2/3\) ,说明在第 8 部分,起点变成:\((len - 1,len/3)\) ,\((x,y)\) 变成 \((len-1-x,y - len/3)\) ,加上 1 2 3 4 5 6 7 部分,也就是 \(cnt*7\)
- 说明在第 9 部分,起点变成 \((len*2/3,len*2/3)\) ,\((x,y)\) 变成 \((x - len*2/3,y-len*2/3)\) ,加上 1 2 3 4 5 6 7 8 部分,也就是 \(cnt*8\)
\(k = 0\) 是停止条件。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll f[200];
ll cal(int k,ll x,ll y) {
if (k == 0) return 1;
ll len = f[k], cnt = f[k * 2]/9;
// printf("k = %d x = %lld y = %lld len = %lld cnt = %lld\n",k,x,y,len,cnt);
if (x < len / 3) {
if (y < len / 3) return cal(k - 1, x, y);
if (y < len * 2 / 3) return cnt + cal(k - 1, len / 3 - 1 - x, y - len / 3);
return cnt * 2 + cal(k - 1, x, y - len / 3 * 2);
} else if (x < len * 2 / 3) {
if (y < len / 3) return cnt * 5 + cal(k - 1, x - len / 3, len / 3 - 1 - y);
else if (y < len * 2 / 3) return cnt * 4 + cal(k - 1, len * 2 / 3 - 1 - x, len * 2 / 3 - 1 - y);
return cnt * 3 + cal(k - 1, x - len / 3, len - 1 - y);
} else {
if (y < len / 3) return cnt * 6 + cal(k - 1, x - len * 2 / 3, y);
else if (y < len * 2 / 3) return cnt * 7 + cal(k - 1, len - 1 - x, y - len / 3);
return cnt * 8 + cal(k - 1, x - len * 2 / 3, y - len * 2 / 3);
}
}
int main() {
f[0] = 1;
for (int i = 1; i <= 39; i++) {
f[i] = f[i - 1] * 3;
}
int k;
ll x1, y1, x2, y2;
scanf("%d%lld%lld%lld%lld", &k, &x1, &y1, &x2, &y2);
ll ans1 = cal(k,x1,y1);
ll ans2 = cal(k,x2,y2);
ll ans = abs(ans1-ans2);
// printf("%lld %lld\n", ans1,ans2);
printf("%lld\n",ans);
return 0;
}



