C. Planar Reflections DP 更加巧妙的一个递推

C. Planar Reflections DP

题目大意：

给你一条射线，他的寿命是 \(k\) ，每次撞击一个平面，如果穿过，则寿命不减，如果反射，则生成一条新的射线，寿命为之前的射线 -1，问给你 \(n\) 个平面，一条寿命为 \(k\) 的射线，最多可以产生多少条新射线。

下面是一个 \(n=2,k=3\) 的样例。

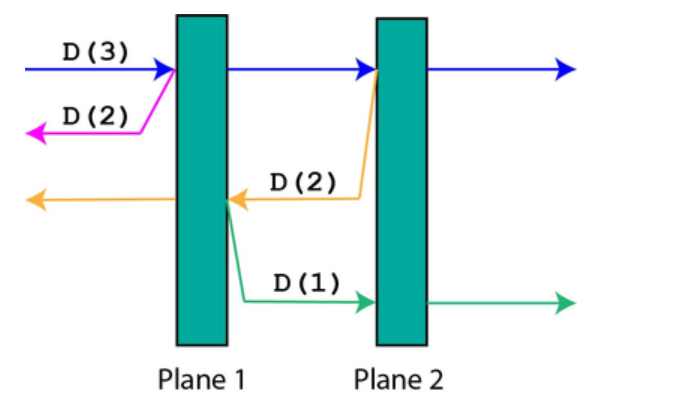
题解：

识别出这个是一个DP是很简单的。

一般的DP会发现当你去推样例的答案的时候，会比较麻烦，尤其是当样例的数据范围略大的时候，但是，你同样也会感觉到有很多重复的推导，可以实现递推，这个也是DP的巧妙之处。

这个题目之前写过一个题解，那算一个非常普通的DP式子。 C. Planar Reflections dp

今天看到一个非常漂亮、巧妙的DP式子。 https://www.bilibili.com/read/cv10541096/

\(dp[i][j]\) 定义光的强度是 \(i\) 前面还有 \(j\) 面镜子最后得到的光线数量。

每次一束强度为k的光穿过镜子，将同时反射出一束强度为k-1的光往反方向照射。

假设一束光强为 \(i\) 的光，前面还有 \(j\) 面镜子，那么这束光最后得到的数量，等价于：一束光强为 \(i-1\) 的光前面有 \(n-j\) 面镜子 得到的光线数 + 一束光强为 \(i\) 的光，前面还有 \(j-1\) 面镜子得到的光线数。

转移方程：\(dp[i][j] = dp[i-1][n-j]+dp[i][j-1]\)

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 1e3 + 10;
const int mod = 1e9 + 7;
LL dp[maxn][maxn];

int main(){
   int T;scanf("%d",&T);
   while(T--){
       int n,k;
       scanf("%d%d",&n,&k);
       for(int i=0;i<=n;i++)
           for(int j=0;j<=k;j++)
               dp[i][j] = 0;

       for(int i=1;i<=k;i++) dp[i][0] = 1;


       for(int i=1;i<=k;i++){
           for(int j=1;j<=n;j++){
                dp[i][j] = (dp[i-1][n-j] + dp[i][j-1])%mod;
           }
       }

       printf("%lld\n",dp[k][n]);
   }
}