C. Planar Reflections dp

C. Planar Reflections dp

题目大意：

给你一条射线，他的寿命是 \(k\) ，每次撞击一个平面，如果穿过，则寿命不减，如果反射，则生成一条新的射线，寿命为之前的射线 -1，问给你 \(n\) 个平面，一条寿命为 \(k\) 的射线，最多可以产生多少条新射线。

下面是一个 \(n=2,k=3\) 的样例。

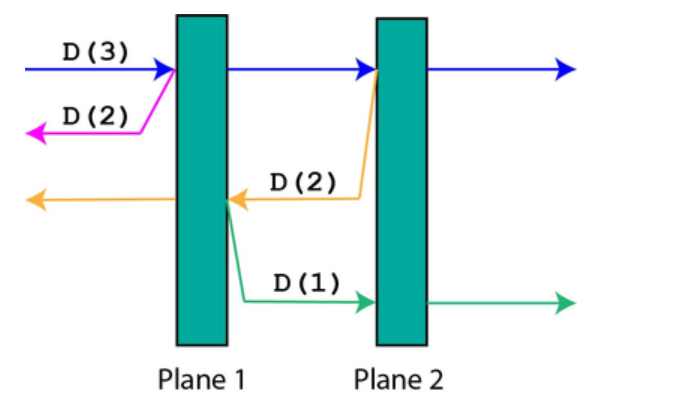
题解：

容易发现这个是一个 \(dp\) ，因为你发现推小数据都是十分复杂的，而且状态和状态之间是有重复的，可以相互转移的。

\(dp[i][j]\) 表示寿命为 \(i\) 通过第 \(j\) 个间隔的数量。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 10;
const int mod = 1e9 + 7;
typedef long long ll;
ll dp[maxn][maxn];

int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        int n, k;
        scanf("%d%d", &n, &k);
        for (int i = 1; i <= k; i++) {
            for (int j = 1; j <= n; j++) {
                dp[i][j] = 0;
            }
        }
//        printf("!!!\n");
        dp[k][1] = 1;
        ll ans = 1;
        for (int i = k - 1; i >= 1; i--) {
            ll sum = 0;
            if ((k - i) & 1) {
                for (int j = 1; j <= n; j++) {
                    sum = (sum + dp[i + 1][j]) % mod;
                    dp[i][j] = sum;
                    ans = (ans + dp[i][j]) % mod;
                }
            } else {
                for (int j = n; j >= 2; j--) {
                    sum = (sum + dp[i + 1][j]) % mod;
                    dp[i][j] = sum;
                    ans = (ans + dp[i][j]) % mod;
                }
            }
        }
        printf("%lld\n",ans);
    }
    return 0;
}