ICPC NEAU Programming Contest 2020 [ 随便置换]

ICPC NEAU Programming Contest 2020 随便置换

题目大意：

中文题就自己看吧

题解：

这个题目还是很复杂的，挺绕的，想说明白也需要很强的表述能力。

• 首先假设 \(a\) 表示原始串，\(c\) 表示目标串，\(p\) 表示置换串，那么题目中已知的等式关系是 \(a=b*p^m\) 求 \(p\)

• 第一步先求 \(p^m\) 这个应该不太难求

  

• 直白的来说就是直接把 \(p^m\) 当作一个置换串 \(s\) ，已知原串和目标串，求这个中间置换串 \(s\)

• 完成第一步之后，这个目标串和原始串就没什么太大的意义了，接下来看这个中间置换串 \(s\)

• \(s\) 也就是 \(p^m\)， 这个是一个变化串，他把 \(a\) 按照本身的变化规律变成了 \(c\) 串。

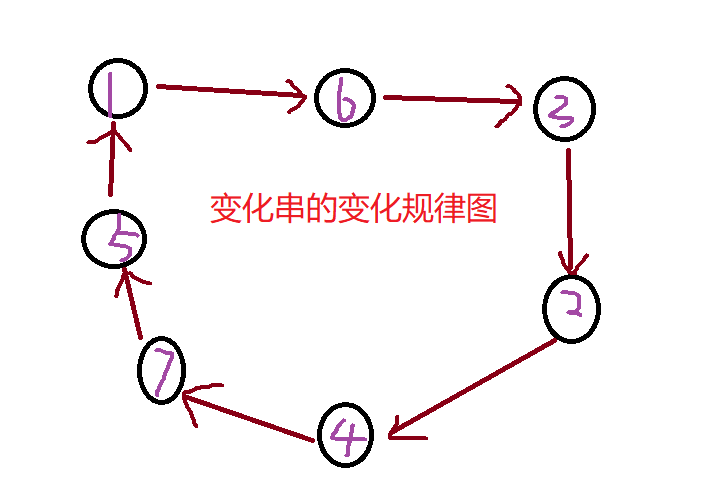
• 接下来说说 \(s\) 串的变化规律：

  • \(s[1]=6\) 表示原来第1个数变成了6

  • \(s[2]=4\) 表示原来第2个数变成了4，\(s[i]\) 表示的原来的第 \(i\) 个变成了第 \(s[i]\)

  • ... 以此类推

  

• 已知 \(s\) 串的变化规律，那么我要求 \(s^2\) 这个串，那是不是相当于原来的 \(s\) 串往后挪了两位，\(s[1]\) 变成了6之后又变成了3，\(s[2]\) 变成了4之后又变成了7，所以可以得到 \(s^2=3745621\) 这个串，这个串的变化规律也很好求，就是原来的串往后挪了两位。

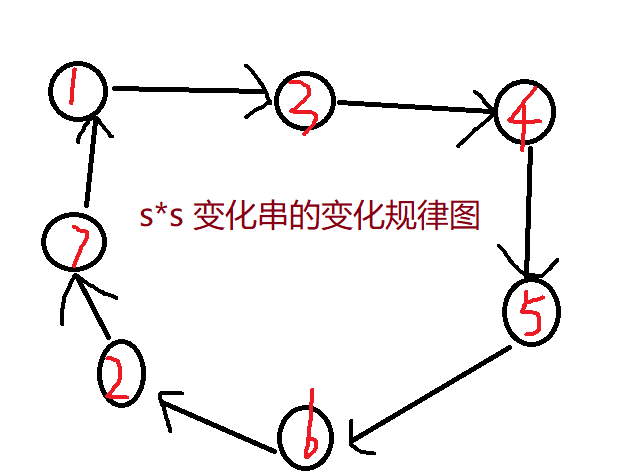
这个图就是上面哪个图两格两格的跳变化出来的图，就是说 \(s\) 串按照 \(s\) 串的规律变化一次之后任选一个起点，之后的第 \(i\) 点是原来的这个点的位置往后跳 \(i*2\)

• 接下来讨论\(p\) 的变化规律，已知 \(p^m=p*p...*p\) ，所以 \(p^m\) 是原来 \(p\) 往后跳 \(m\) 格形成的图。

• 此例题的 \(m=2\) ，先任意选一个起点，假设起点是1：

  • 那么1后面的第 \(m\) 个格子是6，b[2]=6

    b[0] = 1 b[1]=0 b[2]=6 b[3]=0 b[4]=0 b[5]=0 b[6]=0

  • 那么6后面的第 2个格子是3，所以第4个 b[4]=3

    b[0] = 1 b[1]=0 b[2]=6 b[3]=0 b[4]=3 b[5]=0 b[6]=0

  • 以此类推，最后可以得出这个 \(p\) 的变化规律

    b[0] = 1 b[1]=4 b[2]=6 b[3]=7 b[4]=3 b[5]=5 b[6]=2

    

• 这个变化规律图得到之后，就可以求 \(p\) 这串是什么了，这个的求法和之前从串变成规律图操作差不多。

  \(p[1]=4\) \(p[4]=6\) ...

以上都是这个题目的整体求解思路，代码中有部分细节讲解。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+10;
int a[maxn],f[maxn],cnt[maxn],b[maxn],p[maxn];

int Find(int x){
    return x==f[x]?x:f[x]=Find(f[x]);
}

void init(int n){
    for(int i=1;i<=n;i++) f[i]=i,cnt[i]=0;
}
int gcd(int a,int b){
    return b==0?a:gcd(b,a%b);
}

int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int n,m;
        scanf("%d%d",&n,&m);
        init(n);
        for(int i=1,x;i<=n;i++){
            scanf("%d",&x);
            a[x]=i;
            if(Find(i)!=Find(x)){
                f[i]=x;
                /*
                 * 这一步再为求环上的节点数量做准备
                 * 也可以用dfs求环上的节点数量
                 * 但是这些都是简单环，所以用并查集比较简单
                 */
            }
        }
        for(int i=1;i<=n;i++) cnt[Find(i)]++;
        /*
         * a就是p^m这个串
         * cnt[i]表示以i点为根节点的这个环的节点数量
         * 接下来求判断是否有解，因为题目可能不止一个环，所以要判断每一个环的大小是不是都是与m互质
         * 如果不互质，那么不可能找到答案，因为不互质，那么总会有一些点找不到
         */
        int flag = 1;
        for(int i=1;i<=n;i++){
            if(!cnt[i]) continue;
            if(gcd(cnt[i],m)!=1){
                flag = 0;
                break;
            }
        }
        if(!flag){
            printf("NO\n");
            continue;
        }
        /*
         * 判断有解之后就开始求p这个串的变化规律了
         */
//        for(int i=1;i<=n;i++) printf("a[%d]=%d\n",i,a[i]);
        for(int i=1;i<=n;i++){
            if(!cnt[i]) continue;
            int l = cnt[i], w = i;
            for(int j=0;j<l;j++){
                b[j*1ll*m%l] = w;
                w=a[w];
//                printf("b[%d]=%d\n",j*m%l,b[j*1ll*m%l]);
            }
            for(int j=0;j<l;j++){
                p[b[j]]=b[(j+1)%l];
            }
            /*
             * 这里是在求p串，w首先等于i，表示将i定为起点
             * 所以b[0]=w
             * 从这个点往后跳m格b[m]=a[w]
             * 得到b串之后再转化为p串即可
             * !!!注意这个位置p[b[j]]=b[(j+1)%l]
             * 这是因为我存的这个变化串是 a[i] 表示的是原来的第i个变成了第a[i]个
             * 。。。。好像没有讲清楚，自己思考吧，差不多就是怎么变成图的就怎么变回来
             * 假设 原来是 x1->x2 a[x2]=x1
             * 那么之后的 x1->x2  p[x1]=x2
             */
        }
        printf("YES\n");
        for(int i=1;i<n;i++) printf("%d ",p[i]);
        printf("%d\n",p[n]);
    }

}