C. Edgy Trees Codeforces Round #548 (Div. 2) 并查集求连通块

C. Edgy Trees

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a tree (a connected undirected graph without cycles) of nn vertices. Each of the n−1n−1 edges of the tree is colored in either black or red.

You are also given an integer kk. Consider sequences of kk vertices. Let's call a sequence [a1,a2,…,ak][a1,a2,…,ak] good if it satisfies the following criterion:

• We will walk a path (possibly visiting same edge/vertex multiple times) on the tree, starting from a1a1 and ending at akak.
• Start at a1a1, then go to a2a2 using the shortest path between a1a1 and a2a2, then go to a3a3 in a similar way, and so on, until you travel the shortest path between ak−1ak−1 and akak.
• If you walked over at least one black edge during this process, then the sequence is good.

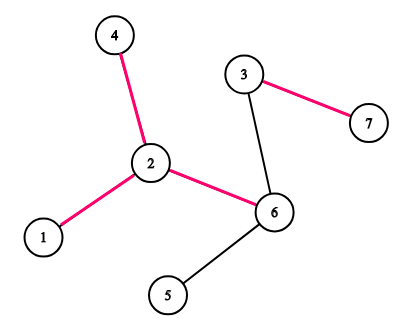
Consider the tree on the picture. If k=3k=3 then the following sequences are good: [1,4,7][1,4,7], [5,5,3][5,5,3] and [2,3,7][2,3,7]. The following sequences are not good: [1,4,6][1,4,6], [5,5,5][5,5,5], [3,7,3][3,7,3].

There are nknk sequences of vertices, count how many of them are good. Since this number can be quite large, print it modulo 109+7109+7.

Input

The first line contains two integers nn and kk (2≤n≤1052≤n≤105, 2≤k≤1002≤k≤100), the size of the tree and the length of the vertex sequence.

Each of the next n−1n−1 lines contains three integers uiui, vivi and xixi (1≤ui,vi≤n1≤ui,vi≤n, xi∈{0,1}xi∈{0,1}), where uiui and vivi denote the endpoints of the corresponding edge and xixi is the color of this edge (00 denotes red edge and 11 denotes black edge).

Output

Print the number of good sequences modulo 109+7109+7.

Examples

input

Copy

4 4
1 2 1
2 3 1
3 4 1

output

Copy

252

input

Copy

4 6
1 2 0
1 3 0
1 4 0

output

Copy

0

input

Copy

3 5
1 2 1
2 3 0

output

Copy

210

Note

In the first example, all sequences (4444) of length 44 except the following are good:

• [1,1,1,1][1,1,1,1]
• [2,2,2,2][2,2,2,2]
• [3,3,3,3][3,3,3,3]
• [4,4,4,4][4,4,4,4]

In the second example, all edges are red, hence there aren't any good sequences.

 

 

这个题目读题读到我绝望，我不太理解这样子的题目。

这个题目我深刻的理解到了两个东西，一个是取模运算，还有一个是并查集求连通块，

这个就是求出有多少个0的连通块，然后用公式求出道路就可以了。

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 100;
const int mod = 1e9 + 7;
bool vis[maxn];
int f[maxn];

int findx(int x)
{
	return f[x] == x ? x : f[x] = findx(f[x]);
}
void unite(int x, int y)
{
	x = findx(x);
	y = findx(y);
	if (x == y) return;
	f[x] = y;
}

int exa[maxn];
int main()
{
	int n, k, num = 0;
	cin >> n >> k;
	ll ans = 1;
	for (int i = 1; i <= k; i++)
	{
		ans *= n;
		ans %= mod;
	}
	//printf("%lld\n", ans);
	memset(vis, 0, sizeof(vis));
	for (int i = 1; i <= n; i++) f[i] = i;
	for (int i = 1; i < n; i++)
	{
		int  a, b, x;
		scanf("%d%d%d", &a, &b, &x);
		if (x) continue;
		unite(a, b);
		if (vis[a] == 0)
		{
			vis[a] = 1;
			num++;
		}
		if (vis[b] == 0)
		{
			vis[b] = 1;
			num++;
		}
	}
	for (int i = 1; i <= n; i++) exa[i] = 0;
	for (int i = 1; i <= n; i++)
	{
		if (vis[i] == 0) continue;
		int x = findx(i);
		exa[x]++;
		//printf("exa[%d]=%d %d\n", x, exa[x],i);
	}
	for (int i = 1; i <= n; i++)
	{
		ll sum = 1;
		if (exa[i] == 0) continue;//printf("%d\n", exa[i]);
		for (int j = 1; j <= k; j++)
		{
			sum *= exa[i];
			sum %= mod;
		}
		//printf("%lld\n", sum);
		ans = (ans - sum + mod) % mod;
	}
	ans = (ans - (n - num) + mod) % mod;
	printf("%lld\n", ans);
	return 0;
}