YbtOJ 「基础算法」 第2章 贪心算法
贪心
A. 【例题1】奶牛晒衣服
[题目背景]
熊大妈决定给每个牛宝宝都穿上可爱的婴儿装 。但是由于衣服很湿,为牛宝宝晒衣服就成了很不爽的事情。于是,熊大妈请你(奶牛)帮助她完成这个重任。
[题目描述]
一件衣服在自然条件下用一秒的时间可以晒干 \(a\) 点湿度。抠门的熊大妈只买了一台烘衣机 。使用用一秒烘衣机可以让一件衣服额外烘干 \(b\) 点湿度(一秒晒干 \(a+b\) 湿度),但在同一时间内只能烘一件衣服。现在有 \(n\) 件衣服,第 \(i\) 衣服的湿度为 \(w_i\)(保证互不相同),要你求出弄干所有衣服的最少时间(湿度为 \(0\) 为干 )。
[输入格式]
第一行三个整数,分别为 \(n,a,b\)。
接下来 \(2\) 到 \(n+1\) 行,第 \(i\) 行输入 \(w_i\)。
[输出格式]
一行,弄干所有衣服的最少时间。
[算法分析]
贪心地取每一次弄干衣服时间最长的衣服来烘干
我们并没有每次都减去整体的晾干值 只是减去了每一次烘干的值 所以while中循环条件应该是\(q.top() - a * ans > 0\)
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
const int N = 1e3 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int n , a , b , ans;
priority_queue <int> q;
signed main()
{
n = read() , a = read() , b = read();
for ( int i = 1 ; i <= n ; i ++ ) q.push(read());
while ( q.top() - a * ans > 0 )
//我们并没有每次都减去整体的晾干值 只是减去了每一次烘干的值
{
ans ++;
int tmp = q.top(); q.pop();
q.push(tmp-b);
}
printf ( "%d" , ans );
return 0;
}
B. 【例题2】雷达装置
[题目描述]
假设海岸线是一条无限延伸的直线。它的一侧是陆地,另一侧是海洋。每一座小岛是在海面上的一个点。雷达必须安装在陆地上(包括海岸线),并且每个雷达都有相同的扫描范围 \(d\)。你的任务是建立尽量少的雷达站,使所有小岛都在扫描范围之内。
数据使用笛卡尔坐标系,定义海岸线为 \(x\) 轴。在 \(x\) 轴上方为海洋,下方为陆地。
[输入格式]
第一行包括 \(2\) 个整数 \(n\) 和 \(d\),\(n\) 是岛屿数目,\(d\) 是雷达扫描范围。
接下来 \(n\) 行,每行两个整数,为岛屿坐标。
[输出格式]
一个整数表示最少需要的雷达数目,若不可能覆盖所有岛屿,输出 -1。
[算法分析]
对于每一个雷达 处理出最左和最右面能控制到它的雷达端点
之后 和线段覆盖思路相似 将雷达按照右端点排序
如果节点的左端点能被前一个放置的雷达覆盖 那么不需要再放置
反之 如果节点的左端点不能被覆盖 那么需要在这个不能被覆盖的节点的右端点放置一个雷达 这样保证了最优
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
const int N = 1e3 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int n , ans;
double d , x , y , last;
struct seg { double l , r; }a[N];//最左面可以放雷达的点 最右面可以放雷达的点
signed main()
{
n = read() , scanf ( "%lf" , &d );
for ( int i = 1 ; i <= n ; i ++ )
{
x = read() , y = read();
if ( d < y ) { printf ( "-1" ); return 0; }
a[i].l = x - sqrt ( d * d - y * y ) , a[i].r = x + sqrt ( d * d - y * y );
}
sort ( a + 1 , a + n + 1 , [](const seg a , const seg b) { return a.r < b.r; } );
last = a[1].r , ans = 1;
for ( int i = 2 ; i <= n ; i ++ )
if ( a[i].l > last )
ans ++ , last = a[i].r;
printf ( "%d" , ans );
return 0;
}
C. 【例题3】畜栏预定
[题目描述]
有\(N\)头牛在畜栏中吃草。每个畜栏在同一时间段只能提供给一头牛吃草,所以可能会需要多个畜栏,给出第\(i\)头牛开始吃草的时间区间\([a_i,b_i]\),求需要的最少畜栏数和每头牛对应的畜栏方案。
[输入格式]
第一行一个正整数\(N\)。
接下来\(N\)行,第\(i\)行两个正整数\(a_i,b_i\)。
[输出格式]
第一行一个整数,表示需要的最少畜栏数。
接下来\(N\)行,第\(i\)行一个整数表示第\(i\)头牛的对应畜栏,编号是从\(1\)开始的连续整数,方案合法即可。
[算法分析]
先将所有区间按照左端点(开始时间)排序
每一次贪心地将这一段区间接到畜栏中结束时间快的畜栏后面 如果接不上就新开一个组
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
const int N = 5e4 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int n , cnt , pos[N];
struct cow { int l , r , id; } a[N];
struct node { int ed , id; const bool operator < ( const node a ) const { return ed > a.ed; } };//保证弹出的是结束时间最小的畜栏
priority_queue <node> q;
signed main ()
{
n = read();
for ( int i = 1 ; i <= n ; i ++ ) a[i].l = read() , a[i].r = read() , a[i].id = i;
sort ( a + 1 , a + n + 1 , [](const cow a , const cow b) { return a.l < b.l; } );
for ( int i = 1 ; i <= n ; i ++ )
{
if ( q.empty() || q.top().ed >= a[i].l ) q.push ( (node) { a[i].r , ++cnt } ) , pos[a[i].id] = cnt;
else
{
pos[a[i].id] = q.top().id;
q.pop();
q.push ( (node) { a[i].r , pos[a[i].id] } );
}
}
printf ( "%d\n" , cnt );
for ( int i = 1 ; i <= n ; i ++ ) printf ( "%d\n" , pos[i] );
return 0;
}
D. 【例题4】荷马史诗
追逐影子的人,自己就是影子 —— 荷马
[题目描述]
Allison 最近迷上了文学。她喜欢在一个慵懒的午后,细细地品上一杯卡布奇诺,静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》 组成的鸿篇巨制《荷马史诗》实在是太长了,Allison 想通过一种编码方式使得它变得短一些。
一部《荷马史诗》中有 \(n\) 种不同的单词,从 \(1\) 到 \(n\) 进行编号。其中第 \(i\) 种单词出现的总次数为 \(w_i\)。Allison 想要用 \(k\) 进制串 \(s_i\) 来替换第 \(i\) 种单词,使得其满足如下要求:
对于任意的 \(1\leq i, j\leq n\) ,\(i\ne j\) ,都有:\(s_i\) 不是 \(s_j\) 的前缀。
现在 Allison 想要知道,如何选择 \(s_i\),才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下,Allison 还想知道最长的 \(s_i\) 的最短长度是多少?
一个字符串被称为 \(k\) 进制字符串,当且仅当它的每个字符是 \(0\) 到 \(k-1\) 之间(包括 \(0\) 和 \(k-1\) )的整数。
字符串 \(str1\) 被称为字符串 \(str2\) 的前缀,当且仅当:存在 \(1 \leq t\leq m\) ,使得 \(str1 = str2[1..t]\)。其中,\(m\) 是字符串 \(str2\) 的长度,\(str2[1..t]\) 表示 \(str2\) 的前 \(t\) 个字符组成的字符串。
[输入格式]
输入的第 \(1\) 行包含 \(2\) 个正整数 \(n, k\) ,中间用单个空格隔开,表示共有 \(n\) 种单词,需要使用 \(k\) 进制字符串进行替换。
接下来 \(n\) 行,第 \(i + 1\) 行包含 \(1\) 个非负整数 \(w_i\),表示第 \(i\) 种单词的出现次数。
[输出格式]
输出包括 \(2\) 行。
第 \(1\) 行输出 \(1\) 个整数,为《荷马史诗》经过重新编码以后的最短长度。
第 \(2\) 行输出 \(1\) 个整数,为保证最短总长度的情况下,最长字符串 \(s_i\) 的最短长度。
[算法分析]
哈夫曼树板题 自下而上构造 用树形结构为每一个节点赋编码
如果你是\(k\)进制的串 那么每一个节点一共有\(k\)个儿子 编码分别为\(0\)到\(k-1\)
基本概念:
-
树的路径长度PL:从树根到树的每个节点的路径长度(每条边长度为1)之和(完全二叉树为这种路径长度最短的二叉树)。
-
树的带权路径长度WPL:树的所有叶子节点的带权路径长度(该节点到根节点路径长度与节点上权的乘积)之和。
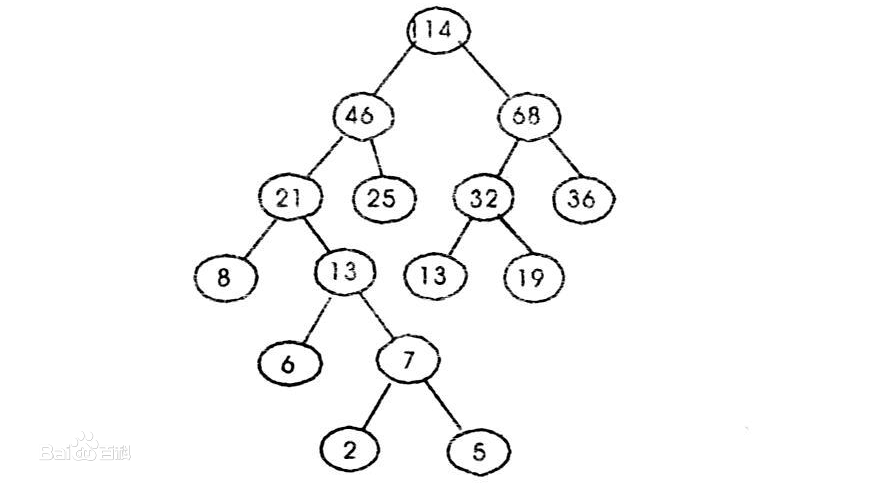
这是一棵典型的二叉哈夫曼树 多叉同理
那么具体代码实现就是:每一次拿出来\(k\)个权值最小的节点并向上合并
可以证明 这样可以保证树上路径权值和(也就是类比石子合并 树根到叶子的路径乘以深度)最小
因为你\(n\)个叶子节点才是需要的 这样可以保证任何一个串不是另一个串的前缀 大的边要尽量向上放 这样才能减少整体文章长度
需要将整棵树补满成完全\(k\)叉树
那么对于循环条件 我们在合并到根之后break即可
#include <bits/stdc++.h>
using namespace std;
#define inl inline
#define int long long
const int N = 1e6 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar(); }
return x * f;
}
struct node
{
int w , dep;
friend bool operator < ( const node &a , const node &b ) { return a.w == b.w ? a.dep > b.dep : a.w > b.w; }
};
priority_queue <node> q;
int n , k , ans;
signed main ()
{
n = read() , k = read();
for ( int i = 1 ; i <= n ; i ++ ) q.push ( (node) { read() , 0 } );
while ( ( q.size() - 1 ) % ( k - 1 ) != 0 ) q.push ( (node) { 0 , 0 } );
while ( q.size() > 1 )//如果小于k了 直接赋值即可
{
int val = 0 , maxdep = 0;
for ( int i = 1 ; i <= k ; i ++ )
{
val += q.top().w;
maxdep = max ( maxdep , q.top().dep );
q.pop();
}
ans += val;
q.push ( (node) { val , maxdep + 1 } );//新建一个父亲节点
}
printf ( "%lld\n%lld" , ans , q.top().dep );
return 0;
}
E. 1.排队接水
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
#define pii pair<int,int>
#define mkp make_pair
#define fi first
#define se second
#define int long long
const int mod = 2147483647;
const int N = 2e6 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int n , ans;
double ave;
struct node { int wait , id , tim; } a[N];
signed main ()
{
n = read();
for ( int i = 1 ; i <= n ; i ++ ) a[i] = { 0 , i , read() };
sort ( a + 1 , a + n + 1 , [](const node &a , const node &b) { return a.tim < b.tim; } );
for ( int i = 1 ; i <= n ; i ++ )
{
printf ( "%d " , a[i].id );
a[i].wait = ans;
ans += a[i].tim;
}
for ( int i = 1 ; i <= n ; i ++ )
ave += a[i].wait;
ave /= (double) n;
printf ( "\n%.2lf" , ave );
return 0;
}
F. 2.砍树问题
[算法分析]
先将树按横坐标排序,则由题意得 \(ai≤min(|pi−pi−1|,|pi+1−pi|)\)。
\(1\)和\(n\)要特判
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
const int N = 2e6 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int ans , n;
struct node { int pos , hei; } a[N];
signed main ()
{
n = read();
for ( int i = 1 ; i <= n ; i ++ ) a[i].pos = read() , a[i].hei = read();
sort ( a + 1 , a + n + 1 , [](const node &a , const node &b) { return a.pos < b.pos; } );
for ( int i = 1 ; i <= n ; i ++ )
{
if ( i == 1 ) ans += max ( 0 , a[i].hei - ( a[i+1].pos - a[i].pos ) );
else if ( i == n ) ans += max ( 0 , a[i].hei - ( a[i].pos - a[i-1].pos ) );
else ans += max ( 0 , max ( a[i].hei - ( a[i].pos - a[i-1].pos ) , a[i].hei - ( a[i+1].pos - a[i].pos ) ) );
}
printf ( "%d" , ans );
return 0;
}
G. 3.出栈序列
[算法分析]
我们对于入栈序列维护一个后缀max
每一次入栈 如果这个值不小于后缀最大值 那么是最大值 pop出来 再尝试pop前一个 以此类推
最后可能没有都pop出来 那么清空栈即可
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
const int N = 1e6 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();如果这个值已经是最大值了 那么pop出来 再尝试pop前一个
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int a[N] , s[N] , n;
stack<int> sta;
int main()
{
n = read();
for ( int i = 1 ; i <= n ; i ++ ) a[i] = read();
for ( int i = n ; i >= 1 ; i -- ) s[i] = max ( s[i+1] , a[i] );//后缀最大值 从后往前,a[i]-a[n]间最大值就是s[i]
for ( int i = 1 ; i <= n ; i ++ )
{
sta.push ( a[i] );
while ( !sta.empty() && sta.top() >= s[i+1] ) printf ( "%d " , sta.top() ) , sta.pop();
//如果这个值已经是最大值了 那么pop出来 再尝试pop前一个
}
//都入栈了 直接输出即可
while ( !sta.empty() ) printf ( "%d " , sta.top() ) , sta.pop();
return 0;
}
H. 4.序列问题
[题目描述]
给定一个长度为\(n\)的数列和一个整数\(k\),求两个长度不小于\(k\)的连续子序列,分别使他们的二进制或运算值和二进制与运算值最大。
[输入格式]
第一行两个正整数 。
第二行\(n\)个整数,表示给定的数列。
[输出格式]
输出\(1\)个整数,分别表示最大的或运算值和最大的与运算值。
[算法分析]
对于或运算 只需要所有点或起来即可
对于与运算 我们必须强制固定选\(k\)长度的子序列 因为这样一定不劣
我们设置\(f[i][j]\)表示第\(i\)个数的第\(j\)位的二进制值
\(sum[i][j]\)表示\(1-i\)这些数的\(j\)位的和
前缀和处理每一个区间内的1 如果1=k 那么合法
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
const int N = 1e6 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int n , k , anshuo , ansyu , a[N] , b[N][31] , sum[N][31];
signed main ()
{
n = read() , k = read();
for ( int i = 1 ; i <= n ; i ++ ) a[i] = read() , anshuo |= a[i];
printf ( "%d " , anshuo );
for ( int i = 1 ; i <= n ; i ++ )
for ( int j = 0 ; j <= 30 ; j ++ )
{
b[i][j] = ( a[i] >> j ) & 1;
sum[i][j] = sum[i-1][j] + b[i][j];
}
for ( int l = 1 ; l <= n - k + 1 ; l ++ )
{
int r = l + k - 1;//越多个数与起来显然要更小 所以严格控制在k个显然不劣
int ans = 0;
for ( int i = 0 ; i <= 30 ; i ++ ) ans += ( 1 << i ) * ( sum[r][i] - sum[l-1][i] == k );
ansyu = max ( ansyu , ans );
}
printf ( "%d" , ansyu );
return 0;
}

