YbtOJ 「基础算法」 第1章 递推算法
A. 【例题1】错排问题
[题目描述]
求多少个\(n\)个数的排列\(A\),满足对于任意的\(i(1\le i\le n) A_i!=i\)。
[输入格式]
一个整数\(n\)。
[输出格式]
一个整数,表示答案。
[算法分析]
我们假设有\(n\)个数 错排方案数为\(f(n)\)
首先 分步计数: 完成\(f(n)\)的统计分两步:将第一封信放进某一个位置 再将其余位置进行排列
- 首先找出一个数\(a\) 这封信不能排在本身位置 只能排在其余\(n-1\)个位置上 因此有\(n-1\)种排法
- 现在讨论其余除\(a\)之外的信的错排
其次 分类计数:假设\(a\)占据了\(b\)的位置 那么\(b\)此时放在哪一个位置分两种情况
- \(b\)放在\(a\)位置上 那么相当于\(a,b\)交换放置 那么剩下\(n-2\)个数进行错排\(f(n-2)\)
- \(b\)不放在\(a\)位置上 那么相当于除了\(a\)之外其他元素的错排问题 那么方案数就是\(f(n-1)\)
根据加法原理 上面的分步计数中第二步的方案数就是\(f(n-1)+f(n-2)\)
那么根据乘法原理 计算结果就是\(f(n)=(n-1)*(f(n-1)+f(n-2))\)
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
#define int long long
const int N = 1e5 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int n , a[N];
signed main()
{
n = read();
a[1] = 0 , a[2] = 1;
for ( int i = 3 ; i <= n ; i ++ )
a[i] = ( i - 1 ) * ( a[i-1] + a[i-2] );
printf ( "%lld" , a[n] );
return 0;
}
B. 【例题2】传球游戏
[题目描述]
上体育课的时候,小蛮的老师经常带着同学们一起做游戏。这次,老师带着同学们一起做传球游戏。
游戏规则是这样的:\(n\)个同学站成一个圆圈,其中的一个同学手里拿着一个球,当老师吹哨子时开始传球,每个同学可以把球传给自己左右的两个同学中的一个(左右任意),当老师再次吹哨子时,传球停止,此时,拿着球没有传出去的那个同学就是败者,要给大家表演一个节目。
聪明的小蛮提出一个有趣的问题:有多少种不同的传球方法可以使得从小蛮手里开始传的球,传了\(m\)次以后,又回到小蛮手里。两种传球方法被视作不同的方法,当且仅当这两种方法中,接到球的同学按接球顺序组成的序列是不同的。比如有三个同学\(1\)号、\(2\)号、\(3\)号,并假设小蛮为\(1\)号,球传了\(3\)次回到小蛮手里的方式有\(1\)->\(2\)->\(3\)->\(1\)和\(1\)->\(3\)->\(2\)->\(1\),共\(2\)种。
[输入格式]
一行,有两个用空格隔开的整数\(n,m(3 \le n \le 30,1 \le m \le 30)\)。
[输出格式]
\(1\)个整数,表示符合题意的方法数。
[算法分析]
我们考虑dp 设\(f[i][j]\)表示当前传球传了\(i\)次 到了\(j\)人手中的方案数
固定小蛮为1号人 则初值\(f[0][1]=1\) 其余都为0
状态转移就是\(f[i][j] = f[i-1][j-1] + f[i-1][j+1]\)
意义为这一个状态的方案数可以由上一次传球到左右两边的人的方案数相加得到
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
#define int long long
const int N = 1e3 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int n , m , f[N][N];//f[i][j]表示球传了i次 最终到了第j个人的方案总数
signed main()
{
n = read() , m = read();//同学人数 传球次数
f[0][1] = 1;//球一次都没传 最终到了第1个人(第一个人为给定的人)
for ( int i = 1 ; i <= m ; i ++ )
{
f[i][1] = f[i-1][n] + f[i-1][2];
for ( int j = 2 ; j < n ; j ++ ) f[i][j] = f[i-1][j-1] + f[i-1][j+1];
f[i][n] = f[i-1][1] + f[i-1][n-1];
}
printf ( "%lld" , f[m][1] );
return 0;
}
C. 【例题3】数的划分
[题目描述]
将整数 \(n\) 分成 \(k\) 份,且每份不能为空,任意两个方案不相同(不考虑顺序)。
例如:\(n=7\),\(k=3\),下面三种分法被认为是相同的。
\(1,1,5\);
\(1,5,1\);
\(5,1,1\).
问有多少种不同的分法。
[输入格式]
\(n,k\) (\(6<n \le 200\),\(2 \le k \le 6\))
[输出格式]
\(1\) 个整数,即不同的分法。
[算法分析]
\(dfs\)和\(dp\)都可以
\(dfs\)的话 因为不能重复 所以考虑按照升序枚举
还需要加一个强力剪枝:即如果剩余的苹果即使每一个都划分成i段 苹果数量也不够的话 就直接剪枝
\(sum + i * ( k - cnt ) \le n\)
如果用\(dp\)做法 那么设置\(f[i][j]\)为\(i\)分成\(j\)个非空的数段的方案数
那么我们分类讨论 常用的方法是讨论1和没有1的情况 这样是为了让两种情况都能写出来表达式
- 有盒子里只装了1个球 那么方案数就是\(f[i-1][j-1]\)
- 没有盒子里只装了1个球 那么所有盒子拿出来一个球 也就是\(i-j\)中分\(j\)段 方案数就是\(f[i-j][j]\)
[代码实现]
dfs:
#include <bits/stdc++.h>
using namespace std;
#define inl inline
const int N = 1e5 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int n , k , ans;
void dfs ( int last , int sum , int cnt ) //上一个划分的段是多少 已经划分了多少个苹果 划分了cnt段
{
if ( cnt == k )
{
if ( sum == n ) return ans ++ , void();
return;
}
for ( int i = last ; sum + i * ( k - cnt ) <= n ; i ++ )
dfs ( i , sum + i , cnt + 1 );
}
signed main()
{
n = read() , k = read();//n分成k份
dfs ( 1 , 0 , 0 );
printf ( "%d\n" , ans );
return 0;
}
dp:
#include <bits/stdc++.h>
using namespace std;
#define inl inline
const int N = 1e3 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int n , k , f[N][N];
signed main()
{
n = read() , k = read();
for ( int i = 1 ; i <= n ; i ++ ) f[i][1] = 1;
for ( int i = 1 ; i <= n ; i ++ )//枚举总值
for ( int j = 2 ; j <= k ; j ++ )//枚举分的段数
if ( i >= j ) f[i][j] = f[i-1][j-1] + f[i-j][j];
//只有总值大于等于段数的时候才可能开始递推
printf ( "%d" , f[n][k] );
return 0;
}
D. 【例题4】栈的问题
[题目背景]
栈是计算机中经典的数据结构,简单的说,栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作,即 pop(从栈顶弹出一个元素)和 push(将一个元素进栈)。
栈的重要性不言自明,任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时,想到了一个书上没有讲过的问题,而他自己无法给出答案,所以需要你的帮忙。
[题目描述]
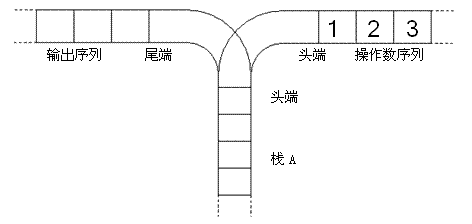
宁宁考虑的是这样一个问题:一个操作数序列,\(1,2,\ldots ,n\)(图示为 1 到 3 的情况),栈 A 的深度大于 \(n\)。
现在可以进行两种操作,
- 将一个数,从操作数序列的头端移到栈的头端(对应数据结构栈的 push 操作)
- 将一个数,从栈的头端移到输出序列的尾端(对应数据结构栈的 pop 操作)
使用这两种操作,由一个操作数序列就可以得到一系列的输出序列,下图所示为由 1 2 3 生成序列 2 3 1 的过程。
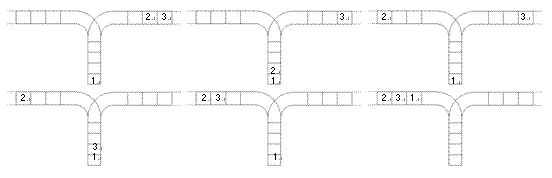
(原始状态如上图所示)
你的程序将对给定的 \(n\),计算并输出由操作数序列 \(1,2,\ldots,n\) 经过操作可能得到的输出序列的总数。
[输入格式]
输入文件只含一个整数 \(n\)(\(1 \leq n \leq 18\))。
[输出格式]
输出文件只有一行,即可能输出序列的总数目。
[算法分析]
我们对于\(1-n\)这个区间 设置\(f_i\)表示\(i\)个数进栈再出栈的方案数
对于每一个\(i\) 在\(1-i\)这段区间内枚举一个断点\(k\) 那么我们把\(k\)左面先出栈再入栈 \(k\)右面先出栈再入栈的方案数相乘
状态转移方程即是:\(f[i] += f[j-1] * f[i-j]\)
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
const int N = 20 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int f[N] , n;//f[i]表示i个数进栈再出栈的方案数
signed main ()
{
n = read();
f[0] = f[1] = 1;
for ( int i = 2 ; i <= n ; i ++ )
for ( int j = 1 ; j <= i ; j ++ )
f[i] += f[j-1] * f[i-j];
printf ( "%d" , f[n] );
return 0;
}
E. 1.划分数列
\(up[i]\)表示以\(i\)为结尾的最长不降子序列的起点
\(down[i]\)同理
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int N = 1e6 + 5;
const int inf = 0x3f3f3f3f;
int read ()
{
int x = 0 , f = 1;
char ch = cin.get();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = cin.get(); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = cin.get(); }
return x * f;
}
int n , a[N] , ans = inf , f[N] , up[N] , down[N];
signed main ()
{
ios::sync_with_stdio(false);
cin.tie(0) , cout.tie(0);
n = read();
for ( int i = 1 ; i <= n ; i ++ ) a[i] = read();
up[1] = down[1] = 1;
for ( int i = 1 ; i <= n ; i ++ )
{
if ( a[i] >= a[i-1] ) up[i] = up[i-1];
else up[i] = i;
if ( a[i] <= a[i-1] ) down[i] = down[i-1];
else down[i] = i;
}
for ( int i = 1 ; i <= n ; i ++ ) f[i] = min ( f[up[i]-1] , f[down[i]-1] ) + 1;
//从上一个分好的段转移过来 再加上这一段的上升/下降
cout << f[n] << endl;
return 0;
}
F. 2.求 f 函数
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
#define int long long
#define mid ((l+r)>>1)
const int N = 2500000+5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int n , f[N] , ans;
void pre ()
{
for ( int i = 1111 ; i > 1000 ; i -- ) f[i] = i - 10;
for ( int i = 1000 ; i ; i -- ) f[i] = f[f[i+11]];
}
signed main ()
{
pre();
n = read();
while ( n )
{
if ( n > 1000 ) ans ^= ( n - 10 );
else ans ^= f[n];
n = read();
}
printf ( "%lld" , ans );
return 0;
}
G. 3.无限序列
[题目描述]
我们按以下方式产生序列:
开始时序列是: 1 ;
每一次变化把序列中的 1 变成 10 ,0 变成 1。
经过无限次变化,我们得到序列 1011010110110101101 ...。
总共有\(Q\)个询问,每次询问为:在区间\(a\)和\(b\)之间有多少个 1。
任务:写一个程序回答\(Q\)个询问。
[输入格式]
输入的第一行为一个整数 ,后面有\(q\)行,每行两个数用空格隔开的整数 。
[输出格式]
输出共\(Q\)行,每行一个回答。
[算法分析]
手搓样例(看题解)可以发现一个性质:
- \(1-3\)区间内\(1\)的个数是\(2\)
- \(1-5\)区间内\(1\)的个数是\(3\)
- \(1-8\)区间内\(1\)的个数是\(5\)
正好符合斐波那契的性质 一个区间内\(1\)的个数就是区间长度的斐波那契数列的前一位的数
那么如果不是整斐波那契数列 那么分解一下即可
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
#define int long long
const int mod = 2147483647;
const int N = 2e6 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int n , a[N] , q , f[N];
int fib ( int x )
{
if ( x == 0 ) return 0;
if ( x == 1 || x == 2 ) return 1;
int i = 1;
for ( i = 1 ; i <= 103 ; i ++ )
if ( f[i] >= x && x > f[i-1] ) break;
return fib(x-f[i-1]) + f[i-2];
}
signed main ()
{
f[0] = f[1] = f[2] = 1;
for ( int i = 3 ; i <= 101 ; i ++ ) f[i] = f[i-1] + f[i-2];
q = read();
for ( int i = 1 , x , y ; i <= q ; i ++ )
{
x = read() , y = read();
printf ( "%lld\n" , fib(y) - fib(x-1) );
}
return 0;
}
H. 4.序列个数
[算法分析]
我们将一个排列看成一个二维矩阵 行坐标表示这个排列中数的下表 列坐标表示第几个数 \(g[i][j]=1\)表示这个排列中第\(i\)个数是\(j\)
对于排列2 3 4 1 5 我们可以得到上图的矩阵
满足a数组的排列需要满足的条件就是在\(1-i\)中 小于等于\(i\)的数恰好为\(a[i]\)个
对应到矩阵中,即以\((1,1)\)为左上角,以\((i,i)\)为右下角的矩阵中,正好有a[i]个1。
然后我们可以考虑从内向外(充矩阵也就是每一次填充一个\(L\)型的区间)填(有后效性,所以要从里往外)
每一行,每一列都只能有1个1.
- \(a_i-a_{i-1}=0\) 这一层不用考虑
- \(a_i-a_{i-1}=1\) 这一层有\(2*i-1\)个位置可以放\(1\) 由于内层已经放了\(a_{i-1}\)个互不相同的\(1\) 那么第\(i\)层必然减少了\(2*a_{i-1}\)个位置
- \(a_i-a_{i-1}=2\) 则这两个\(1\)必然在两条臂上 那么每条臂上剩余的位置就是\(i-1-a_{i-1}\)
- \(a_i-a_{i-1}\ge 3\) 显然不能填写
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define inl inline
#define int long long
const int mod = 340610;
const int N = 2e6 + 5;
inl int read ()
{
int x = 0 , f = 1;
char ch = getchar();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = getchar (); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = getchar (); }
return x * f;
}
int n , a[N];
signed main ()
{
scanf ( "%d" , &n );
for ( int i = 1 ; i <= n ; i ++ ) a[i] = read();
for ( int i = 1 ; i <= n ; i ++ )
{
if ( a[i] - a[i-1] == 1 ) ans *= 2 * i - 1 - 2 * a[i-1];
if ( a[i] - a[i-1] == 2 ) ans *= pow ( i - 1 - a[i-1] , 2 ) ;
if ( a[i] - a[i-1] >= 3 ) { ans = 0; break; }
ans %= mod;
}
printf ( "%lld" , ans );
return 0;
}
I. 5.等距跳跃
[算法分析]
暴力枚举所有点对并沿着两点路径跳 如果合法就更新答案
坑点1:必须跳出去 所以在这个点不能被跳的时候cnt要清零
坑点2:初始点必须为边界点(也就是这个点对跳一步必然可以跳出去 否则不是边界点 需要加特判)
[代码实现]
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int N = 5e3 + 5;
const int inf = 0x3f3f3f3f;
int read ()
{
int x = 0 , f = 1;
char ch = cin.get();
while ( !isdigit ( ch ) ) { if ( ch == '-' ) f = -1; ch = cin.get(); }
while ( isdigit ( ch ) ) { x = ( x << 1 ) + ( x << 3 ) + ( ch ^ 48 ); ch = cin.get(); }
return x * f;
}
int n , m , q , x[N] , y[N] , ans = -inf , vis[N][N];
int check ( int xx , int yy ) { return 1 <= xx && xx <= n && 1 <= yy && yy <= m; }
signed main ()
{
ios::sync_with_stdio(false);
cin.tie(0) , cout.tie(0);
n = read() , m = read() , q = read();
for ( int i = 1 ; i <= q ; i ++ ) x[i] = read() , y[i] = read() , vis[x[i]][y[i]] = 1;
for ( int i = 1 ; i <= q ; i ++ )
for ( int j = 1 ; j <= q ; j ++ )
{
if ( i == j ) continue;
int dx = x[j] - x[i] , dy = y[j] - y[i] , posx = x[i] , posy = y[i];
if ( check ( posx - dx , posy - dy ) ) continue;
int cnt = 0;
while ( check ( posx , posy ) )
{
if ( vis[posx][posy] ) posx += dx , posy += dy , cnt ++;
else { cnt = 0; break; }
}
ans = max ( ans , cnt );
}
cout << ans;
return 0;
}
}

