图解数据结构——二叉查找树/二叉排序树

 

什么是二叉查找树？

二叉查找树又叫二叉排序树。它是一种树型数据结构。抽象成图片如下图：

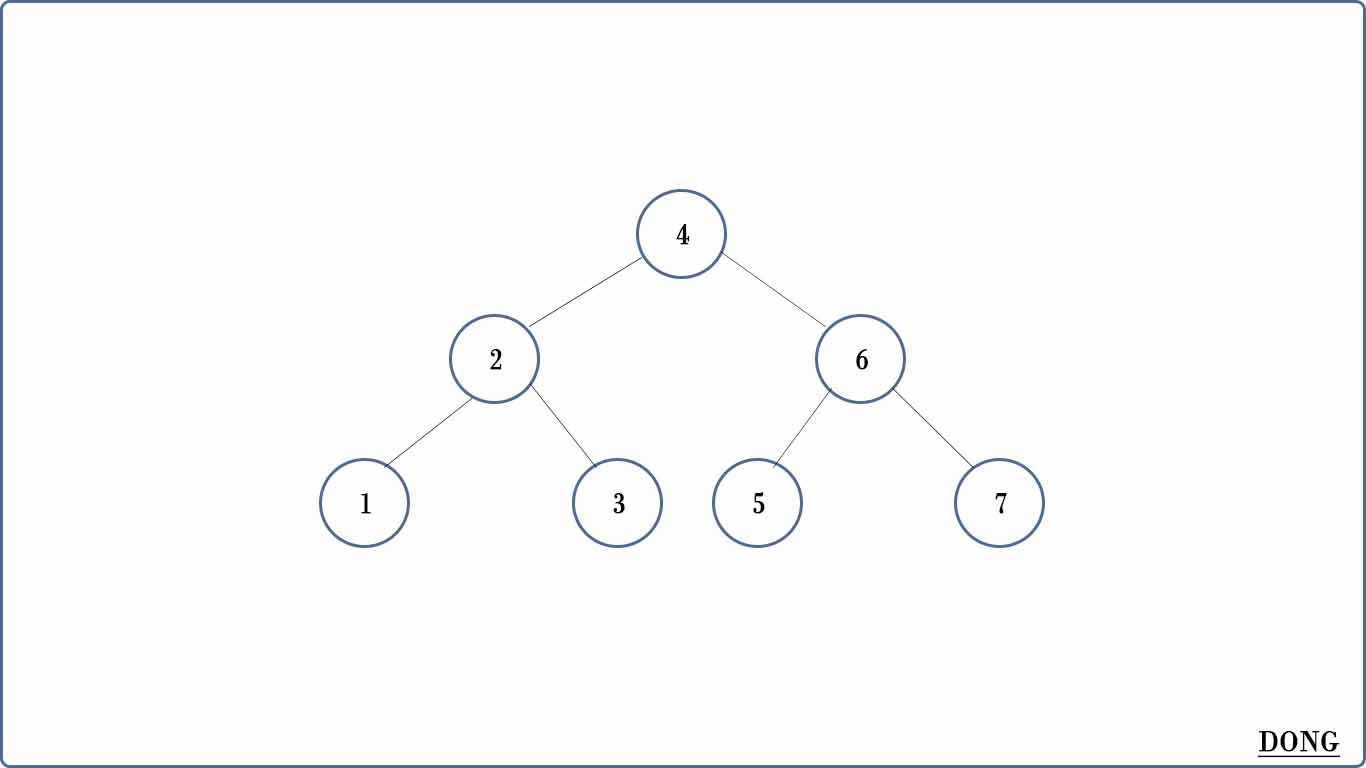
二叉树有以下特点：

1、任意节点的左子节点都小于它。

2、任意节点的右子节点都大于它。

3、任意节点的左右子树都是二叉查找树。（其实满足上面两点也就基本满足了这个）

 

小提示：为什么二叉查找树要有上面的这三个特点呢？因为如果具有了这三个特点的，那么这棵树就相当于存储了一个排序好的数据了。这样在查找的时候，就能使用二分法进行查找。如果不知道什么是二分法，建议先稍微理解一下二分法是怎么查找数据的。简单来说就是在一组排序好的数据中每次查找的时候都把需要查找的数据分成两份。比如在[1,2,3,4,5]中查找4，第一次查找就把1到5分成两份，比对3。如果比3大那么在把3后面的分成两份再比较中间的，依次套娃。

 

二叉查找树有什么优点呢？

二叉查找树可以让我们更快的在一堆数据中找到想要的某个数据。

举个例子：

上图的二叉查找树中存有[1,2,3,4,5,6,7]这7个数据，每个数据代表一个节点，我现在要在这7个数据查到3这个数据。查找步骤如下：

1、首先，跟根节点的4比较，发现3<4，所以下一步查找4节点的左孩子2节点。（为什么要查找左孩子，参照上面二叉树的的特点1）

2、跟2节点比较，发现3>2，所以下一步查找2节点的右孩子3节点。（为什么要查找右孩子，参照上面二叉树的的特点2）

3、跟3节点比较，发现3=3，至此对比三次，找到想要的数据了。

从上面的例子我们看出来，在七个数据中查找“3”我们只查找了三次。

二叉查找树利用了二分法的思想。在一个二叉查找树中查找所需的数据，最大查找次数等于二叉树的高度。（如上面例子中的树的高度是3，很容易理解什么是树的高度）

 

二叉查找树怎么插入数据呢？

向二叉查找树中插入数据和在其中查找数据类似，依次对比，然后按照二叉树的特点插入指定位置。

比如在上面的二叉查找树中插入8。

 

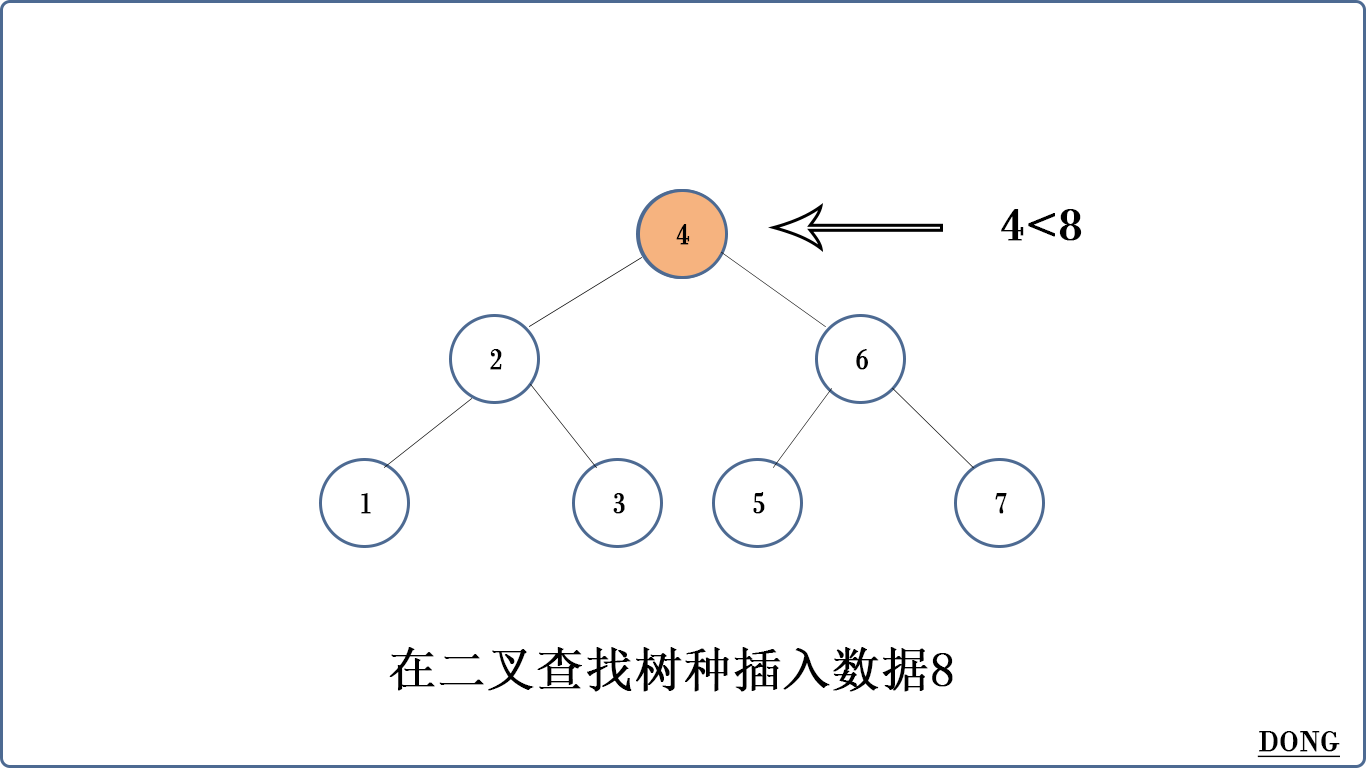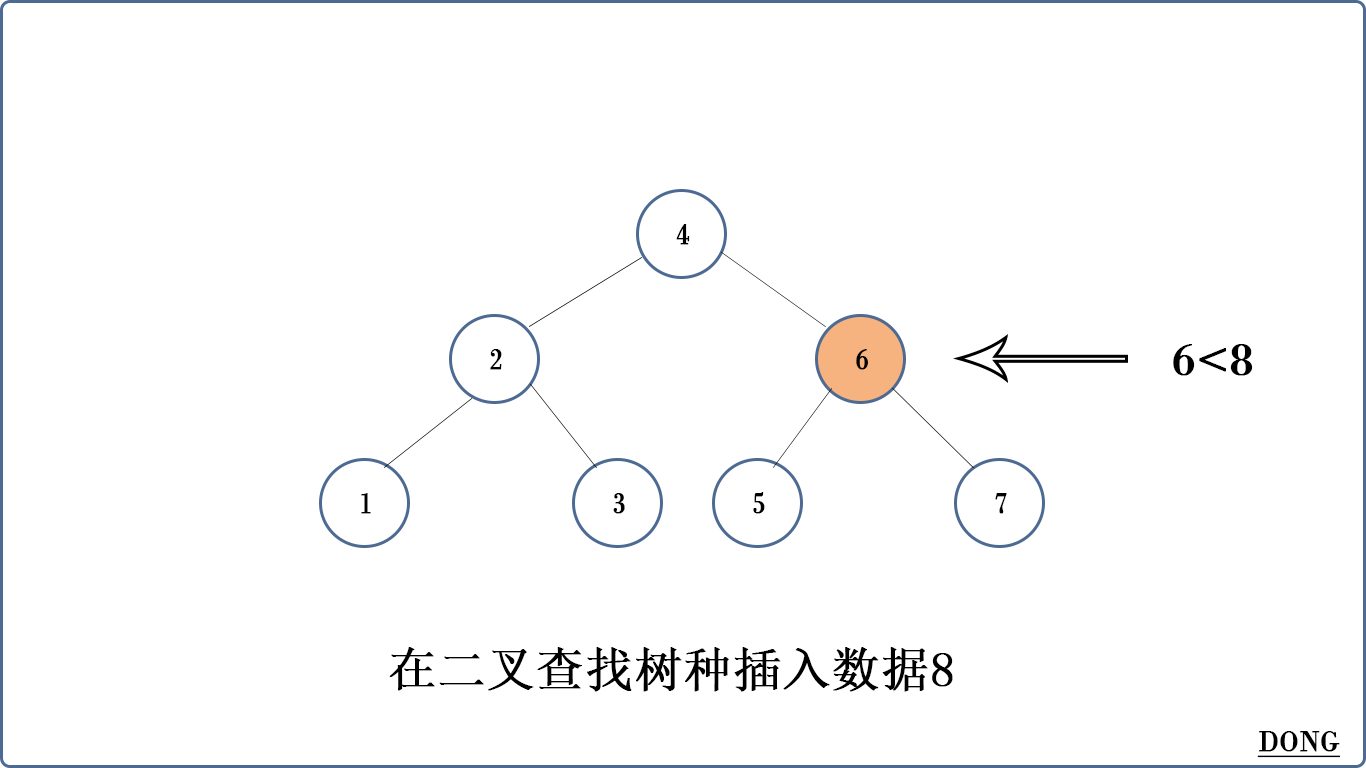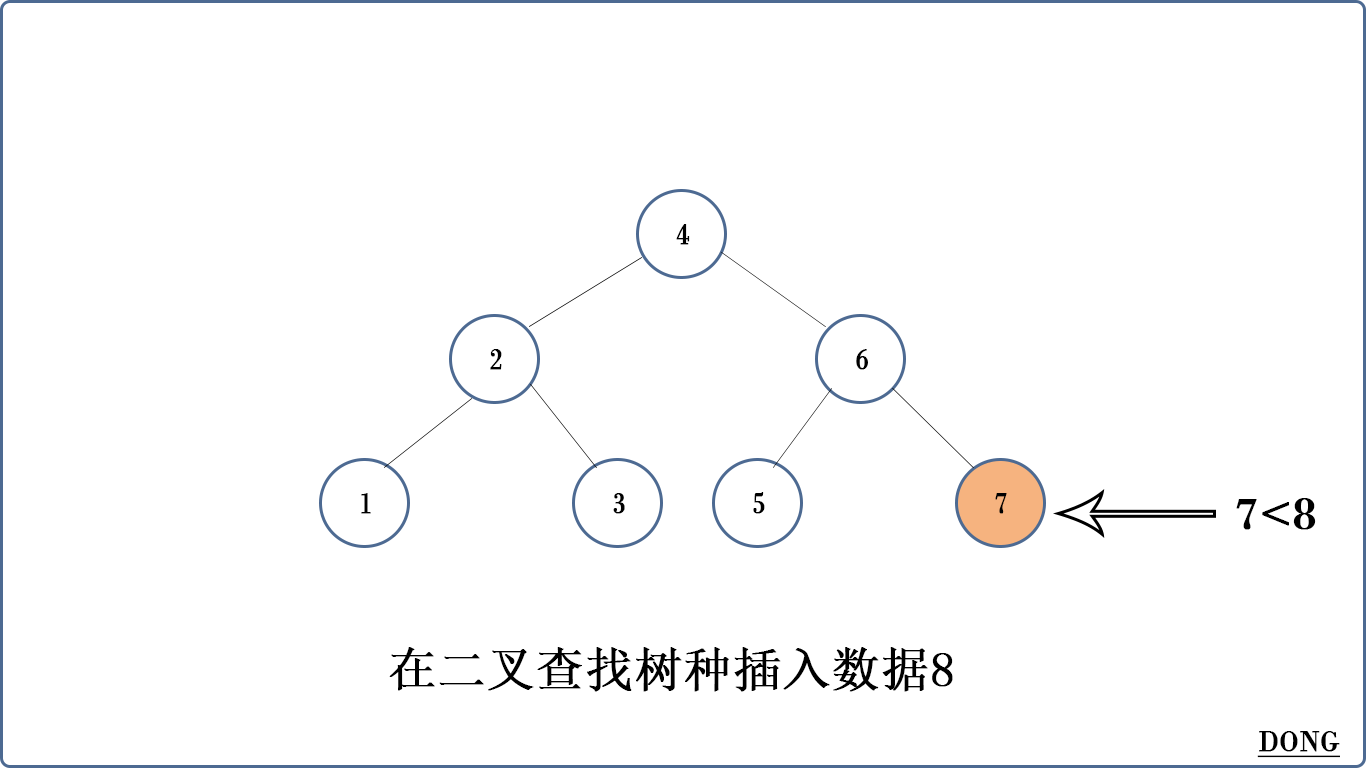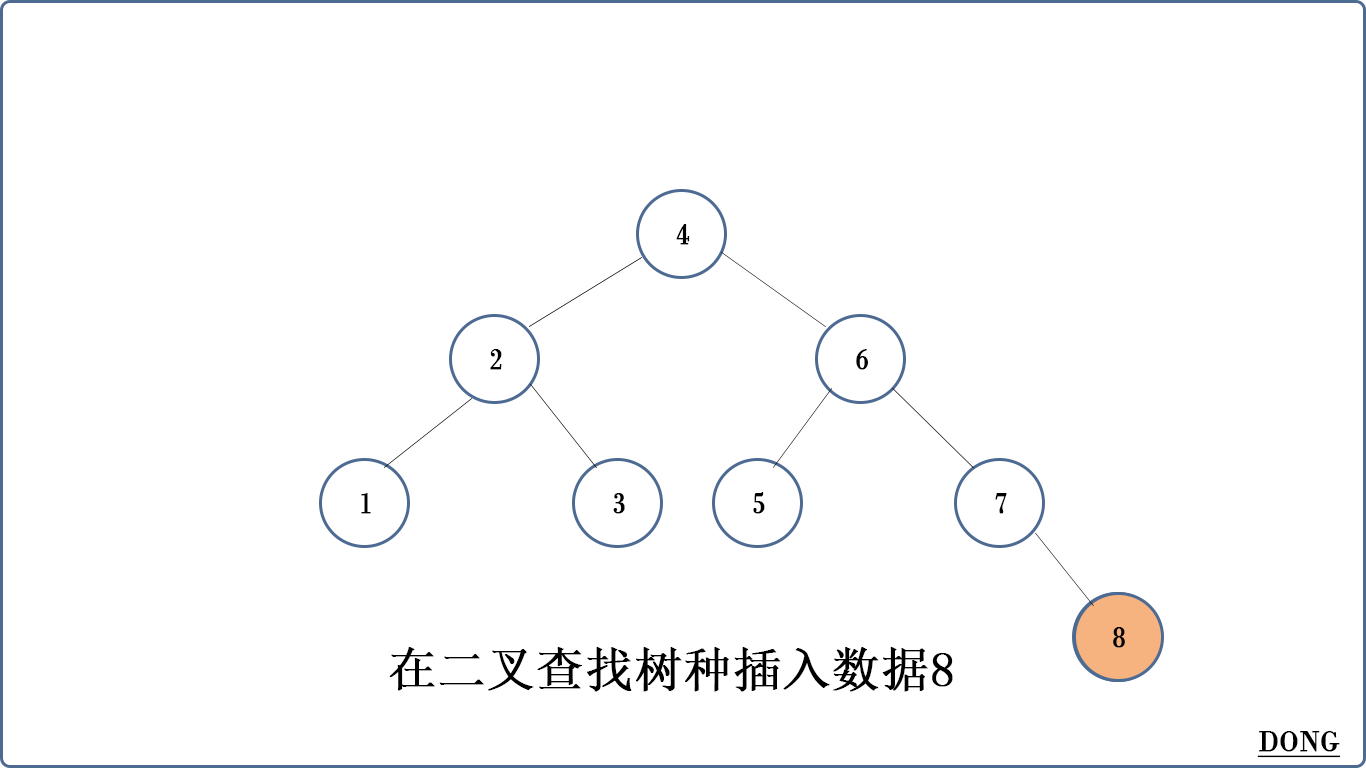
二叉查找树有什么缺陷嘛？

当然有，如果你只按照上面的特点去用代码实现一个二叉查找树，那么是会有缺点的。

来举个例子：

首先给一个初始的二叉查找树，如下图：

我们使用上面的方法插入一个数字6。

再添加7、8、9。

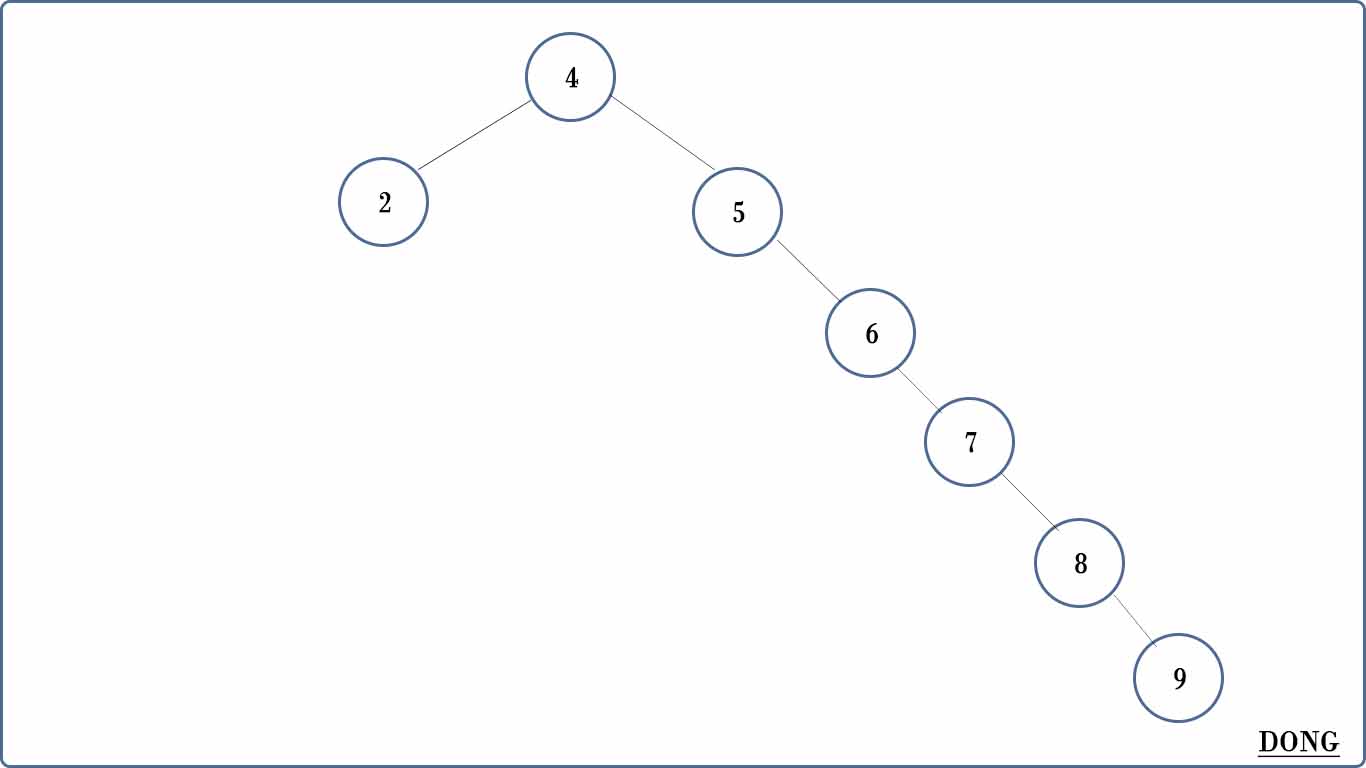
这样，所有的节点就倾向于同一边了，都快变成一个链表了。

这样就失去了二叉查找树的优点了，查找效率特别低下。

 

怎么解决这些缺陷呢？

我们可以结合平衡的概念，将二叉查找树升级成（avl）平衡二叉查找树。

下一篇文章继续（avl）平衡二叉树。二叉查找树就先不用代码实现了，因为实现了，使用的时候也有很多缺陷。

介绍完了平衡二叉查找树会提供平衡二叉查找树的代码实现。

---

 如果你发现了什么问题，欢迎提出意见，我们共同进步。

 end...