Atcoder Typical DP Contest S - マス目(状压 dp+剪枝)
介绍一个不太主流的、非常暴力的做法(
首先注意到 \(n\) 非常小,\(m\) 比较大,因此显然以列为阶段,对行的状态进行状压。因此我们可以非常自然地想到一个非常 trivial 的做法:\(dp_{i,mask1,mask2}\) 表示考虑到第 \(i\) 列,当前列状态为 \(mask1\),当前列中能从左上角到达的点集为 \(mask2\),枚举下一列状态简单转移一下即可。
但是相信聪明的读者到这里一定可以发现,这个做法是错误的,因为题目规定可以朝四个方向走,也就是说有可能出现如下图所示的情况:
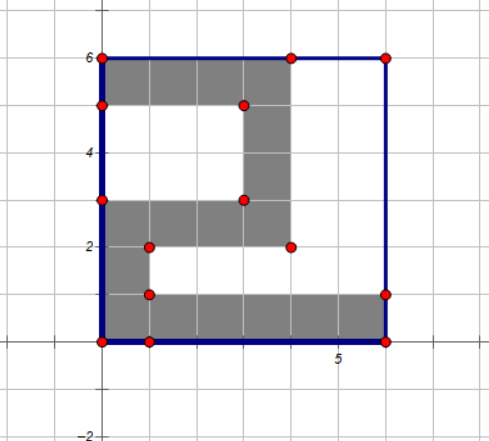
对于下图中的情况,当我们状态转移到第四列时,我们会判定 \(1,2,3,4\) 行是可以从起点到达的,而由于前一列(第 \(3\) 列)的第 \(6\) 行在前三行组成的子矩形中无法从起点到达,因此我们也会判断第四列第 \(6\) 行无法从源点到达,也就导致了情况的漏算。
怎么处理呢?由于这种情况的存在,我们要在状态中多记录一些东西,注意到这个 \(n=6\) 有点小的出奇,\(\dbinom{6}{2}\) 不过 \(15\),因此考虑对每个点对 \((j,k)\) 记录当前列中这两行的格子在前 \(i\) 列组成的子矩形中是否连通,即设 \(dp_{i,j,k}\) 表示前 \(i\) 列中两两可达性为 \(j\),\(k\) 中的格子可以从 \((1,1)\) 到达的方案数。这样一来我们在枚举下一列状态并 check 每个点是否能从 \((1,1)\) 到达时可以考虑这样的做法:对于每个 \(j\),如果它左边的格子能从 \((1,1)\) 到达并且它是黑格,那么它能从 \((1,1)\) 到达,否则如果 \(\exists k\) 满足 \((j,k)\) 在前 \(i\) 列组成的子矩形中连通并且 \(k\) 能从 \((1,1)\) 到达,那么 \(j\) 能从 \((1,1)\) 到达,正确性显然。而显然如果我们知道了上一列的两两之间的可达性,是可以用传递闭包 or 并查集直接推出上一列的可达性的,因此这个做法恰好能够解决我们之前遇到的问题。
复杂度?最坏情况下该算法的复杂度可以达到 \(2^{15}\times 2^6\times 2^6\times 100\times 6^3\approx 3\times 10^{12}\)(这要是能过我就当场把这个电脑屏幕 **),然鹅这个复杂度是远远达不到上界的,因为首先对于这 \(2^{15}\) 个表示可达性的状态中,一个状态合法当且仅当它的传递闭包就是它本身,暴力枚举一下可知这 \(2^{15}\) 个状态中总共只有 \(203\) 个合法的状态,这下复杂度降到了 \(203\times 2^6\times 2^6\times 100\times 6^3\approx 2\times 10^{10}\),其次在 DP 过程中很多状态是转移不到的,因此如果某个 \(dp_{i,j,k}=0\) 那么我们就不用转移了,加上这个小小的优化之后速度又能快不少。此题 \(\text{TL}=8\text{s}\),而我这个做法只跑了 \(222\text{ms}\)。当然这肯定不是最快的版本,还有优化的空间,比方说一开始大可不必 \(\mathcal O(2^{15}\times 6^3)\) 枚举所有状态,可以一遍 DFS 一遍把不合法的状态剪掉,这样程序还可以跑得更快(虽然这不是复杂度瓶颈所在),以及在转移中,由于本题的图是无向图,传递闭包可以用 dsu 来代替,这样可将 \(6^3\) 变成 \(6^2\),但由于本人懒癌症晚期就没有进一步优化了(
const int MAXM=100;
const int MAXT=1<<6;
const int MAXP=1<<15;
const int MAX_ST=203;
const int MOD=1e9+7;
void add(int &x,int v){((x+=v)>=MOD)&&(x-=MOD);}
int n,m,id[MAXP+5],msk[MAXP+5],cnt=0,is[8][8],pre_is[8][8],blk[8];
int dp[MAXM+5][MAXT+5][MAX_ST+5];
int main(){
scanf("%d%d",&n,&m);int lim=1<<(n*(n-1)/2);
for(int i=0;i<lim;i++){
int cur=i;bool flg=1;
for(int j=1;j<=n;j++) for(int k=1;k<j;k++)
is[j][k]=is[k][j]=cur&1,cur>>=1;
for(int j=1;j<=n;j++) is[j][j]=1;
for(int j=1;j<=n;j++) for(int k=1;k<=n;k++) for(int l=1;l<=n;l++)
if(is[j][k]&&is[k][l]&&!is[j][l]) flg=0;
if(flg) msk[++cnt]=i,id[i]=cnt;
} //printf("%d\n",cnt);
for(int i=0;i<(1<<n);i++){
if(~i&1) continue;
int pre=0,msk1=0,msk2=0;memset(is,0,sizeof(is));
for(int j=1;j<=n;j++){
if(~i>>(j-1)&1){
for(int k=pre+1;k<j;k++) for(int l=pre+1;l<k;l++) is[k][l]=is[l][k]=1;
if(!pre) for(int k=pre+1;k<j;k++) msk1|=(1<<k-1);
pre=j;
}
} if(!pre) msk1=(1<<n)-1;
for(int k=pre+1;k<=n;k++) for(int l=pre+1;l<k;l++) is[k][l]=1;
for(int k=n;k;k--) for(int l=k-1;l;l--) msk2=msk2<<1|is[k][l];
// printf("%d %d\n",msk1,msk2);
add(dp[1][msk1][id[msk2]],1);
}
for(int i=1;i<m;i++){
for(int j=1;j<(1<<n);j++){
for(int k=1;k<=cnt;k++){
// printf("%d %d %d %d\n",i,j,k,dp[i][j][k]);
if(!dp[i][j][k]) continue;int cur=msk[k];
for(int l=1;l<=n;l++) for(int o=1;o<l;o++)
pre_is[l][o]=pre_is[o][l]=cur&1,cur>>=1;
for(int l=0;l<(1<<n);l++){
for(int o=1;o<=n;o++) blk[o]=l>>(o-1)&1;
int pre=0;memset(is,0,sizeof(is));
for(int o=1;o<=n;o++){
if(!blk[o]){
for(int p=pre+1;p<o;p++) for(int q=pre+1;q<p;q++)
is[p][q]=is[q][p]=1;
pre=o;
}
}
for(int p=pre+1;p<=n;p++) for(int q=pre+1;q<p;q++)
is[p][q]=is[q][p]=1;
for(int p=1;p<=n;p++) if(blk[p])
for(int q=1;q<p;q++) if(blk[q])
is[p][q]|=pre_is[p][q],is[q][p]|=pre_is[q][p];
for(int p=1;p<=n;p++) if(blk[p])
for(int q=1;q<=n;q++) if(blk[q])
for(int r=1;r<=n;r++) if(blk[r])
is[q][r]|=is[q][p]&is[p][r];
int msk1=0,msk2=0;
for(int p=1;p<=n;p++){
bool flg=0;
if(blk[p]&&(j>>p-1&1)) flg=1;
else if(blk[p]){
for(int q=1;q<=n;q++) if(is[p][q]&&(j>>q-1&1))
flg=1;
} msk1|=flg<<(p-1);
}
for(int p=n;p;p--) for(int q=p-1;q;q--)
msk2=msk2<<1|is[p][q];
// printf("%d %d %d -> %d %d %d(%d)\n",i,j,msk[k],i+1,msk1,msk2,id[msk2]);
add(dp[i+1][msk1][id[msk2]],dp[i][j][k]);
}
}
}
} int ans=0;
for(int j=1;j<(1<<n);j++) if(j>>(n-1)&1)
for(int k=1;k<=cnt;k++) add(ans,dp[m][j][k]);
printf("%d\n",ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号