李超树学习笔记
由于最近在忙 whk,利用二模考完的空挡刚好学完了这个 trick。因此这大概是我初中阶段学的最后一个算法了(?)
李超线段树可以支持以下两个操作:
- 插入一条直线/线段 \(y=kx+b(l\le x\le r)\)
- 查询 \(x=x_0\) 与插入的直线/线段交点纵坐标的最大值
当然这里要求满足 \(l,r,x_0\in\mathbb{Z}\),因为我们要以它们为下标建立线段树,否则就是我也不知道怎么做了(London fog
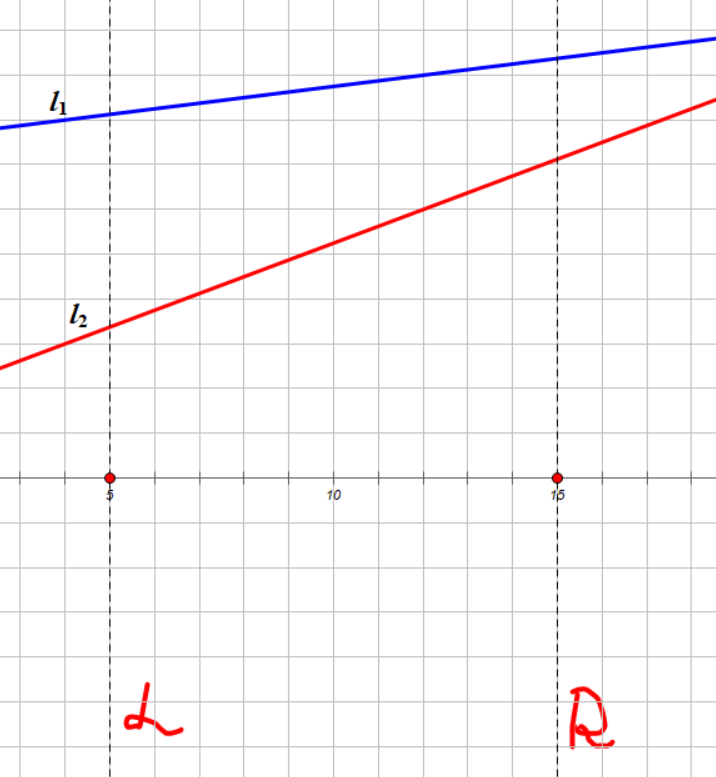
我们考虑以 \(x\) 轴坐标为下标建一棵线段树。线段树上一个区间 \([l,r]\) 上维护一个叫做优势最大线段的量表示在最高那段折线中横坐标跨度最大的线段,比方说对于下图:

优势最大线段(直线)即为绿色直线。
现在考虑插入一段线段(直线)\(y=kx+b(l\le x\le r)\) 后对区间的优势最大线段产生怎样的影响。首先按照线段树的套路将 \([l,r]\) 拆成线段树上若干个区间 \([l_i,r_i]\),然后考虑依次处理这些区间优势最大线段的改变,我们不妨紧盯其中一个区间 \([L,R]\),记 \([L,R]\) 原先的优势最大线段为 \(l_1\),新插入的线段为 \(l_2\),分情况讨论:
- 如果 \(l_1\) 原本就不存在,那直接令 \([L,R]\) 的优势最大线段为 \(l_2\) 即可,简单易懂(
- 如果 \(l_1\) 在 \([L,R]\) 中的部分完全高于 \(l_2\),那 \(l_2\) 简直就是来搞笑的,直接
return即可,简单易懂(
- 如果 \(l_1\) 在 \([L,R]\) 中的部分完全低于 \(l_2\),那原本 \(l_1\) 暴露在最高折线的部分会全部被 \(l_2\) 取代,因此 \(l_2\) 就成了最大优势线段,而 \([L,R]\) 左右儿子的优势最大线段也分别有可能变为 \(l_2\),也就是说如果按照朴素的解法来我们需要递归左右儿子更新,复杂度显然爆炸,不过借鉴标记永久化的思想可以将这个标记保留在这个节点处,不往下
pushdown了——反正最后用 \(x=x_0\) 截函数图像等价于求 \([x_0,x_0]\) 的最大优势线段,是个单点查询,可以通过查询 \([x_0,x_0]\) 及其祖先的最大优势线段在 \(x=x_0\) 处的值并取个 \(\max\) 搞定。

-
如果 \(l_1\) 在 \([L,R]\) 的部分一边高于 \(l_2\),一边低于 \(l_2\),我们考虑交点位置进一步分情况讨论(或者考虑 \(mid=\lfloor\dfrac{L+R}{2}\rfloor\) 处 \(l_1,l_2\) 交点纵坐标 \(m_1,m_2\) 的大小关系)
-
如果 \(m_1\le m_2\)
继续分情况:
-
如果 \(l_1\le l_2\),那么 \(l_2\) 并没有取代 \(l_1\) 在 \([L,R]\) 的最大优势线段的地位,但是有可能 \(l_2\) 取代了 \(l_1\) 在 \([L,mid]\) 处的最大优势线段的位置,因此我们可以拿 \(l_2\) 继续去更新 \([L,R]\) 的左儿子并递归下去。这样保证对于 \(x_0\in[L,R]\),我们在计算 \(x_0\) 处的答案时 both \(l_1\) and \(l_2\) 的贡献都能被计算到。

-
如果 \(l_1>l_2\),那么 \(l_2\) 取代了 \(l_1\) 在 \([L,R]\) 的最大优势线段的地位,并且由于标记永久化,当计算 \(x\in[L,R]\) 时 \(l_2\) 的贡献是肯定会被计算进去了,但 \(l_1\) 就不一定了,对于某些 \(x_0\),\(l_1\) 是吊打得了 \(l_2\) 的(现在写题解真的有 yyq&wc 内味了),因此 \(l_1\) 还是应当被考虑进去的,并且显然这样的 \(x_0\) 都集中在左半部,因此我们:
- 先用 \(l_1\) 更新 \([L,mid]\)
- 将 \([L,R]\) 的最大优势线段赋为 \(l_2\)

-
-
如果 \(m_1>m_2\)
镜像?-
若 \(l_1\le l_2\)
和 \(m_1\le m_2\) 里的第二类类似,只不过变为递归右区间。

-
若 \(l_1>l_2\)
和 \(m_1\le m_2\) 里的第一类类似,只不过变为递归右区间。

-
-
修改部分的代码大概长这样(这里我是通过取交点+判断交点在 \(mid\) 左边还是右边进行分类的,当然也可以直接求在 \(mid\) 处的函数值,代码大同小异,并无太大区别):
void modify(int k,int l,int r,seg x){
int mid=s[k].l+s[k].r>>1;
if(l<=s[k].l&&s[k].r<=r){
if(!s[k].mx.id) return s[k].mx=x,void();
double l1=s[k].mx.ask(s[k].l),r1=s[k].mx.ask(s[k].r);
double l2=x.ask(s[k].l),r2=x.ask(s[k].r);
if(l2<=l1&&r2<=r1) return;
if(l1<=l2&&r1<=r2) return s[k].mx=x,void();
double ix=(s[k].mx.b-x.b)/(x.k-s[k].mx.k);
if(ix<=mid){
if(l1<=l2) modify(k<<1,l,r,x);
else modify(k<<1,l,r,s[k].mx),s[k].mx=x;
} else {
if(l1<=l2) modify(k<<1|1,l,r,s[k].mx),s[k].mx=x;
else modify(k<<1|1,l,r,x);
} return;
}
if(r<=mid) modify(k<<1,l,r,x);
else if(l>mid) modify(k<<1|1,l,r,x);
else modify(k<<1,l,mid,x),modify(k<<1|1,mid+1,r,x);
}
其次是第二种操作,事实上理解了插入操作后查询操作就异常容易了,只需将根到 \([x_0,x_0]\) 路径上所有区间的最大优势线段 \(x_0\) 处的值取个 \(\max\) 即可。
模板题代码:
const int LIM=39989;
const double EPS=1e-6;
int n,lstans,tot;
struct seg{
double k,b;int id;
seg(double _k=0,double _b=0,double _id=0):k(_k),b(_b),id(_id){}
double ask(int x){return k*x+b;}
};
struct node{int l,r;seg mx;} s[LIM*4+5];
void build(int k,int l,int r){
s[k].l=l;s[k].r=r;s[k].mx=seg();if(l==r) return;
int mid=l+r>>1;build(k<<1,l,mid);build(k<<1|1,mid+1,r);
}
void modify(int k,int l,int r,seg x){
int mid=s[k].l+s[k].r>>1;
if(l<=s[k].l&&s[k].r<=r){
if(!s[k].mx.id) return s[k].mx=x,void();
double l1=s[k].mx.ask(s[k].l),r1=s[k].mx.ask(s[k].r);
double l2=x.ask(s[k].l),r2=x.ask(s[k].r);
if(l2<=l1&&r2<=r1) return;
if(l1<=l2&&r1<=r2) return s[k].mx=x,void();
double ix=(s[k].mx.b-x.b)/(x.k-s[k].mx.k);
if(ix<=mid){
if(l1<=l2) modify(k<<1,l,r,x);
else modify(k<<1,l,r,s[k].mx),s[k].mx=x;
} else {
if(l1<=l2) modify(k<<1|1,l,r,s[k].mx),s[k].mx=x;
else modify(k<<1|1,l,r,x);
} return;
}
if(r<=mid) modify(k<<1,l,r,x);
else if(l>mid) modify(k<<1|1,l,r,x);
else modify(k<<1,l,mid,x),modify(k<<1|1,mid+1,r,x);
}
seg query(int k,int p){
if(s[k].l==s[k].r) return s[k].mx;int mid=s[k].l+s[k].r>>1;
seg cur=(p<=mid)?query(k<<1,p):query(k<<1|1,p);
if(s[k].mx.id==0) return cur;if(cur.id==0) return s[k].mx;
double x=cur.ask(p),y=s[k].mx.ask(p);
if(x>y||(fabs(x-y)<EPS&&cur.id<s[k].mx.id)) return cur;
else return s[k].mx;
}
int main(){
scanf("%d",&n);build(1,1,LIM);
for(int i=1;i<=n;i++){
int opt;scanf("%d",&opt);
if(opt==1){
int x0,y0,x1,y1;scanf("%d%d%d%d",&x0,&y0,&x1,&y1);
x0=(x0+lstans-1)%LIM+1;y0=(y0+lstans-1)%1000000000+1;
x1=(x1+lstans-1)%LIM+1;y1=(y1+lstans-1)%1000000000+1;
if(x0>x1) x0^=x1^=x0^=x1,y0^=y1^=y0^=y1;
if(x0==x1) modify(1,x0,x1,seg(0,max(y0,y1),++tot));
else{
double k=1.*(y1-y0)/(x1-x0),b=y1-x1*k;
modify(1,x0,x1,seg(k,b,++tot));
}
} else {
int ps;scanf("%d",&ps);ps=(ps+lstans-1)%LIM+1;
seg tt=query(1,ps);printf("%d\n",lstans=tt.id);
}
}
return 0;
}
最后再稍微多说几句关于“最大优势线段”的问题,someone(including me)may argue that 有可能出现插入一个线段前不是最大优势线段,但插完某个线段后就变成最大优势线段的情况,比方说下图,在插入红、橙两条线段(在图中是直线,下同)前橙色不是最大优势线段,插入蓝色线段后就变成最大优势线段了。

但事实上我们大可不必真的这么纠结于这个“最大优势线段”的定义,或者说,这个“最大优势线段”给这个定义是方便理解这个算法,事实上这个问题还要牵扯到“贡献是否有可能被算到”来解答,即如果 \([L,R]\) 的最大优势线段为 \(l\),那么 \(l\) 可能会对 \(x_0\in[L,R]\) 的答案产生贡献。比方说在上面第四种情况的第二种情况,我们明知 \(l_1\) 在 \([mid+1,R]\) 处完全被 \(l_2\) 吊打了,我们就索性将整个区间的最大优势线段赋为 \(l_2\) 表示 \(l_2\) 会对整个区间产生贡献就完事了,但 \(l_1\) 还有可能对左边 \([L,mid]\) 产生贡献,因此我们还需继续递归左区间(u1s1 有很多关于李超树的题解,不过大概像我一样对这个最大优势线段讲解得这么细致入微的是少之又少罢)
李超树插入复杂度是 \(n\log^2n\),因为要拆成 \(\log n\) 个区间,每个区间又有可能往下递归 \(\log\) 层。查询复杂度依旧是 \(n\log n\)。
李超树一般应用于斜率优化,是替代 CDQ 分治/平衡树维护凸壳的不错选择,当然也会有出题人强行套个树剖之类的,下面是李超树的一些应用。
例题:
1. P4097 [HEOI2013]Segment
mol ban tea,直接建个李超线段树随便维护一下就完事了,注意特判 \(x_1=x_2\) 的情况
2. P4254 [JSOI2008]Blue Mary开公司
Cu Li,唯一不同的是读入方式+最后答案要除以 \(100.0\)(((
3. P4655 [CEOI2017]Building Bridges
首先很明显有一个朴素的 \(dp\) 转移方程:\(dp_i\) 表示连到 \(i\) 所花费的最小代价,那么显然 \(dp_i=\min\limits_{j=1}^{i-1}\{dp_j+(h_i-h_j)^2+s_i-s_j\}\),其中 \(s\) 为 \(g\) 数组的前缀和。
斜率优化显然可行。不过既然是李超树学习笔记那咱就要用好写的李超树来实现呗。稍微变个形可得 \(dp_i=h_i^2+s_i+\min\limits_{j=1}^{i-1}\{-2h_ih_j+dp_j+h_j^2-s_j\}\),如果记 \(k_j=-2h_j,b_j=dp_j+h^2_j-s_j\),那么后面那东西就是一个 \(\min\{k_jh_i+b_j\}\) 的形式,李超树维护一下即可,复杂度 \(n\log H\),其中 \(H=\max\{h_i\}\)
4. CF631E Product Sum
直接算价值似乎有点困难,我们不妨从增量的角度进行计算,总价值最大意味着增量最大,因此我们只需求出最大的增量即可。
首先求出 \(a\) 数组的前缀和 \(s\),我们考虑将 \(i\) 元素移动到了 \(j\) 号元素前面的贡献——这里我们假设 \(j<i\)。将 \(i\) 移到 \(j\) 前面之后,\([j,i-1]\) 中全部元素都会向后移一格,而 \(a_i\) 会向前提 \(i-j\) 格,因此变化量即是 \(-(i-j)a_i+s_{i-1}-s_{j-1}\),我们不妨枚举 \(j\),那么这个贡献就是 \(-s_{j+1}+\max\limits_{i>j}\{ja_i-ia_i+s_{i-1}\}\),这又是一个 \(kx+b\) 的形式,李超树维护一下即可。另一半也同理,只不过这里可以将 \(j\) 的定义改为将 \(i\) 移到 \(j\) 后面,这样就不会错过将 \(a_i\) 移到序列末尾的情况了,贡献即为 \((j-i)a_i-(s_j-s_i)\),也可用类似的方式维护。
5. P4069 [SDOI2016]游戏
李 超 上 树(London fog
其实也挺套路的罢……
把树进行 HLD,那么每次链上加数操作即可转化为对 \(\log n\) 条 DFS 序区间,在这些 DFS 区间中每个点 \(u\) 上加入一个数 \(C=kd_u+b\),其中 \(d_u\) 表示 \(u\) 离根的距离,\(k,b\) 为常数——这个直接求出 LCA,然后分 \(u\to\text{LCA},v\to\text{LCA}\) 的情况分别跳下重链即可,具体来说对于 \(u\to\text{LCA}\),加入直线的 \(k=-A,b=ad_u+B\),对于 \(v\to\text{LCA}\),加入直线的 \(k=A,b=a(d_s-2d_{\text{LCA}})+B\),其中 \(A,B\) 为读入的两个参数。与普通李超树不太一样的是这题还需要支持区间求 \(\min\),并且这里不是简单地以 DFS 序下标为横坐标,而是变化不太规则的距离,这个看似有点难处理,不过注意到对于一段重链上的点,它们到根节点的距离肯定是递增的,因此对于每段区间上的每条直线,它取到最小值的地方肯定是这段区间的一个端点,因此只需再额外维护一个 \(mn\) 表示这段区间中的所有直线上的所有点的最小值,上推就取两个端点之一计算贡献即可。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号