FFT/NTT复习笔记&多项式&生成函数学习笔记Ⅰ
众所周知,tzc 在 2019 年(12 月 31 日)就第一次开始接触多项式相关算法,可到 2021 年(1 月 1 日)才开始写这篇 blog。
感觉自己开了个大坑(
多项式
多项式乘法
好吧这个应该是多项式各种运算中的基础了。
首先,在学习多项式乘法之前,你需要学会:
复数
我们定义虚数单位 \(i\) 为满足 \(x^2=-1\) 的 \(x\)。
那么所有的复数都可以表示为 \(z=a+bi\) 的形式,其中 \(a,b\) 均为实数。
复数的加减直接对实部虚部相加减就行了。
复数的乘法稍微用下乘法分配律就有 \((a+bi)(c+di)=(ac-bd)+(ad+bc)i\)
复平面
我们以实部为横坐标,虚部为纵坐标建立平面直角坐标系,我们称得到的平面为“复平面”,这样所有复数 \(z=a+bi\) 都可以用复平面上的一个点 \((a,b)\) 表示。
例如 \((1,0)\) 就表示 \(1\),\((-1,1)\) 就表示 \(-1+i\)
定义复数的模长为其所表示的点与原点间的距离,即 \(|z|=\sqrt{a^2+b^2}\)
我们知道,高中阶段会学两种坐标系,一是平面直角坐标系,二是极坐标系。前面我们提到的 \((a,b)\) 就是 \(z\) 在平面直角坐标系下的坐标,据此也可类比出 \(z\) 在极坐标系下的坐标 \((r,\theta)\)。显然 \(r\) 就是复数 \(z\) 的模长,\(\theta\) 为复数 \(z\) 所表示的向量 \((a,b)\) 与 \(x\) 轴正半轴的夹角,我们称之为幅角。
根据三角函数显然有 \(a=r\cos\theta,b=r\sin\theta\)
考虑将两个用极坐标表示的复数 \((r_1,\theta_1),(r_2,\theta_2)\) 相乘:
\((r_1,\theta_1)(r_2,\theta_2)\)
\(=(r_1\cos\theta_1+r_1\sin\theta_1i)(r_2\cos\theta_2+r_2\sin\theta_2i)\)
\(=(r_1r_2\cos\theta_1\cos\theta_2-r_1r_2\sin\theta_1\sin\theta_2)+(r_1r_2\sin\theta_1\cos\theta_2+r_1r_2\cos\theta_1\sin\theta_2)i\)
\(=r_1r_2(cos(\theta_1+\theta_2)+\sin(\theta_1+\theta_2))=(r_1r_2,\theta_1+\theta_2)\)
于是我们得到复数乘法的原则:模长相乘,幅角相加。
单位根
定义 \(n\) 次单位根为满足 \(z^n=1\) 的复数 \(z\)。
考虑什么样的复数 \(z\) 满足条件,假设 \(z\) 写成极坐标形式为 \((r,\theta)\),那么 \(z^n=(r^n,n\theta)\)。
而 \(z^n=(1,0)\)。故这样的复数的模长均为 \(1\),幅角乘 \(n\) 为 \(2\pi\) 的整数倍。
故 \(r=1,\theta=\dfrac{2k\pi}{n}\),其中 \(k\) 为整数。
定义 \(\omega_n^i\) 为 \((1,\dfrac{2i\pi}{n})=\cos(\dfrac{2i\pi}{n})+i\sin(\dfrac{2i\pi}{n})\)。
单位根有如下性质(由于都比较显然就不一一证明了):
- \(\omega_n^i=\omega_n^{i+n}\)
- \(\omega_n^i=(\omega_n^1)^i\)
- 若 \(n\) 为偶数,则 \(\omega_n^i=-\omega_n^{i+n/2}\)
- \(\omega_n^i=\omega_{n/2}^{i/2}\)
单位根反演
qwq 这东西在三周前 XES 讲母函数的时候曾经讲过
单位根反演就是如下等式:
\([i\equiv 0\pmod{n}]=\dfrac{1}{n}\sum\limits_{t=0}^{n-1}(\omega_n^{i})^t\)
证明:
若 \(i\) 不是 \(n\) 的倍数,则 \(\omega_i\neq 1\),\(\dfrac{1}{n}\sum\limits_{t=0}^{n-1}(\omega_n^{i})^t=\dfrac{(\omega_n^i)^n-1}{\omega_n^i-1}\),由于 \((\omega_i)^n-1=0,\omega_i-1\neq 0\),故原式 \(=0\)。
若 \(i\) 是 \(n\) 的倍数,则 \(\omega_i=1\),式子中每项都是 \(1\),加起来除以 \(n\) 就是 \(1\)。
下面终于进入正题了:
快速傅里叶变换
对于多项式 \(A(x)=\sum\limits_{i=0}^na_ix^i,B(x)=\sum\limits_{i=0}^nb_ix^i\),设 \(C(x)=A(x)B(x)=\sum\limits_{i=0}^{n+m}c_ix^i\)
那么显然 \(c_i=\sum\limits_{x+y=i}a_xb_y\)
设 \(N\) 为大于 \(n+m\) 且最小的满足 \(N=2^k\)(\(k\) 为整数)的 \(N\)
由于 \(N>n+m\),所有 \(x+y=i\) 等价于 \(x+y-i\equiv 0\pmod{N}\)
至于 \(N\) 为什么要是 \(2\) 的整数次幂,后面再说。
继续推式子:
\(c_i=\sum\limits_{x+y-i\equiv 0\pmod{N}}a_xb_y\)
\(=\sum\limits_{x,y}a_xb_y\times\dfrac{1}{N}\sum\limits_{t=0}^{N-1}(\omega_N^{x+y-i})^t\)
\(=\dfrac{1}{N}\sum\limits_{x,y}\sum\limits_{t=0}^{N-1}\omega_N^{(x+y-i)t} a_xb_y\)
\(=\dfrac{1}{N}\sum\limits_{x,y}\sum\limits_{t=0}^{N-1}\omega_N^{-it} a_x\omega_N^{xt}b_y\omega_N^{yt}\)
\(=\dfrac{1}{N}\sum\limits_{t=0}^{N-1}\omega_N^{-it} \times\sum\limits_{x}a_x\omega_N^{xt}\times\sum\limits_{y}b_y\omega_N^{yt}\)
记 \(\hat{a}_t=\sum\limits_{i}a_i\omega_{N}^{it},\hat{b}_t=\sum\limits_{i}b_i\omega_{N}^{it}\),i.e,\(a_t\) 是将 \(\omega_N^t\) 代入多项式 \(A\) 后计算得到的结果,\(b_t\) 是将 \(\omega_n^t\) 代入多项式 \(B\) 后计算得到的结果。
则 \(c_i=\dfrac{1}{N}\sum\limits_{t=0}^{N-1}\omega_N^{-it} \hat{a}_t\hat{b}_t\)
稍微观察一下即可发现,若记 \(d_t=\hat{a}_t\hat{b}_t\),那么 \(c_i\) 就是 \(\omega_N^{-i}\) 代入多项式 \(D\) 后计算得到的结果。
是不是感觉与前面计算 \(\hat{a}_t,\hat{b}_t\) 的过程如出一辙?只不过 \(\omega_{N}^t\) 变成了 \(\omega_{N}^{-t}\) ?并且最后系数除了个 \(N\)?
故我们只需考虑计算 \(\hat{a}_t,\hat{b}_t\) 的过程,根据 \(\hat{a}_t,\hat{b}_t\) 计算 \(c_i\) 的过程同理即可。
考虑分治地计算 \(\hat{a},\hat{b}\)。
将 \(a\) 按照下标分为奇数和偶数两部分,每部分都是一个长为 \(\dfrac{N}{2}\) 的数组,不妨设两个数组为 \(a_{0,i}\) 和 \(a_{1,i}\),其中 \(a_{0,i}=a_{2i},a_{1,i}=a_{2i+1}\)
那么显然有 \(\hat{a}_t=\sum\limits_{i=0}^{N/2-1}\omega_{N}^{2it}a_{0,i}+\sum\limits_{i=0}^{N/2-1}\omega_{N}^{(2i+1)t}a_{1,i}\)。
把右边的 \(\omega_N^{(2i+1)t}\) 拆成 \(\omega_{N}^{2it}\times \omega_{N}^t\) 可得:
\(\hat{a}_t=\sum\limits_{i=0}^{N/2-1}\omega_{N}^{2it}a_{0,i}+\omega_{N}^t\sum\limits_{i=0}^{N/2-1}\omega_{N}^{2it}a_{1,i}\)
而由 \(\omega_i^n=\omega_{i/2}^{n/2}\) 得 \(\hat{a}_t=\sum\limits_{i=0}^{N/2-1}\omega_{N/2}^{it}a_{0,i}+\omega_{N}^t\sum\limits_{i=0}^{N/2-1}\omega_{N/2}^{it}a_{1,i}\)
设 \(\hat{a}_{0,t}=\sum\limits_{i=0}^{N/2-1}\omega_{N/2}^{it}a_{0,i},\hat{a}_{1,t}=\sum\limits_{i=0}^{N/2-1}\omega_{N/2}^{it}a_{1,i}\)
分治地计算 \(\hat{a}_{0,i},\hat{a}_{0,1}\)
最后 \(\hat{a}_t=\hat{a}_{0,t}+\omega_{N}^t\hat{a}_{1,t}\)
由于我们要保证每次 \(N/2\) 都可以除尽,所以我们选择将 \(N\) 定为 \(2\) 的整数次幂。
不过注意,按照定义域这里的 \(t\) 是在 \([0,N/2-1]\) 范围内的,因此对于 \(t\in[0,N/2-1]\) 才能用这个式子计算。不过注意到 \(\hat{a}_{t+N/2}=\hat{a}_{0,t}+\omega_N^{t+N/2,N}\hat{a}_{1,t}=\hat{a}_{0,t}-\omega_{N}^t\hat{a}_{1,t}\),用这个公式可以计算出 \(\hat{a}_{t+N/2}\)
上述推理过程写成代码的形式如下:
const int MAXN=1<<21;//pay sepcial attention to array size
struct comp{
double x,y;//(real,imag)
comp(){x=y=0;}
comp(double _x,double _y){x=_x;y=_y;}
friend comp operator +(comp lhs,comp rhs){return comp(lhs.x+rhs.x,lhs.y+rhs.y);}
friend comp operator -(comp lhs,comp rhs){return comp(lhs.x-rhs.x,lhs.y-rhs.y);}
friend comp operator *(comp lhs,comp rhs){return comp(lhs.x*rhs.x-lhs.y*rhs.y,lhs.x*rhs.y+lhs.y*rhs.x);}
} f[MAXN+5],g[MAXN+5],h[MAXN+5];
const double Pi=acos(-1);//the value of Pi
int n,m,LEN=1;//LEN is the smallest N such that N>n+m and N=2^k (k is integer)
void FFT(comp *a,int len,int type){
if(len==1) return;//the point value of a constant is the constant itself
comp a0[len>>1],a1[len>>1];//a0[i] and a1[i]
for(int i=0;i<len;i+=2) a0[i>>1]=a[i],a1[i>>1]=a[i+1];
FFT(a0,len>>1,type);FFT(a1,len>>1,type);//find the value of \hat{a}_0 and \hat{a}_1
comp W=comp(cos(2*Pi/len),type*sin(2*Pi/len)),w=comp(1,0);//omega_{len}^1
for(int i=0;i<len;i++,w=w*W){
if(i<(len>>1)) a[i]=a0[i]+w*a1[i];
else a[i]=a0[i-(len>>1)]+w*a1[i-(len>>1)];
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<=n;i++) scanf("%lf",&f[i].x);
for(int i=0;i<=m;i++) scanf("%lf",&g[i].x);
while(LEN<=(n+m)) LEN<<=1;
FFT(f,LEN,1);FFT(g,LEN,1);
for(int i=0;i<LEN;i++) h[i]=f[i]*g[i];
FFT(h,LEN,-1);for(int i=0;i<=n+m;i++) printf("%d ",(int)(h[i].x/LEN+0.5));//remember to divide c[i] by N
return 0;
}
在上面的代码中,有一些点需要注意:
-
FFT 数组的大小需要注意,假设两个多项式长度最大值分别为 \(n,m\),那么你所开数组的大小应至少为 \(2^{\lceil\log_2(n+m)\rceil}\)
-
最后别忘了将数组中所有值除以 \(N\)。
迭代 FFT
由于 FFT 常数很大,需要进行优化。
如图所示,我们手推一下递归的过程,先将其分成了 \(0,2,4,6\) 和 \(1,3,5,7\) 两组,又将 \(0,2,4,6\) 分成了 \(0,4\) 和 \(2,6\) 两组,将 \(1,3,5,7\) 分成了 \(1,5\) 和 \(3,7\) 两组。
然后对 \(0,4\) 进行合并,\(2,6\) 进行合并,\(1,5\) 进行合并,\(3,7\) 进行合并;然后合并长度为 \(4\) 的区间 \(0,4,2,6\) 和 \(1,5,3,7\),最后合并长度为 \(8\) 的区间 \(0,4,2,6,1,5,3,7\)。
于是我们考虑把 \(a_0,a_1,a_2,\dots,a_8\) 交换位置交换到 \(a_0,a_4,a_2,a_6,a_1,a_5,a_3,a_7\) 的位置。
然后合并长度为 \(2\) 的区间 \([2i,2i+1]\),再合并 \(4\) 的区间 \([4i,4i+3]\),然后是 \(8\) 的区间,以此类推。
那么变换前的下标和变换后的下标有什么规律呢?
不难发现 \(1\) 的二进制是 \(001\),\(4\) 的二进制是 \(100\),\(1\) 与 \(4\) 二进制下刚好互为翻转串。然后你发现 \(2\) 与 \(2\),\(3\) 与 \(6\),\(5\) 与 \(5\) 也有这样的规律。
因此我们就可以得出这样的规律:变换后下标为 \(i\) 的数在原来的 \(a_i\) 中的下标在二进制下互为翻转串。
至于怎么求 \(i\) 变换后的下标 \(rev_i\),暴力地 \(n\log n\) 求肯定是 ok 的。不过考虑到常数的原因,最好用类似数位 \(dp\) 的方法达到 \(O(n)\) 的复杂度。
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(LOG-1));
这样我们就有了不用递归的实现方式:
void FFT(comp *a,int len,int type){
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=1;i<len;i<<=1){
comp W=comp(cos(Pi/i),type*sin(Pi/i));
for(int j=0;j<len;j+=i*2){
comp w(1,0);
for(int k=0;k<i;k++,w=w*W){
comp x=a[j+k],y=w*a[i+j+k];
a[j+k]=x+y;a[i+j+k]=x-y;
}
}
}
}
通过以上探究,我们学会了 FFT,它有不少优点,譬如它能在高效地求出两个多项式的卷积。但同时它也有许多缺点,例如使用 FFT 可能会出现精度问题(因为使用了 double),并且它也不支持取模等等。那假如我们真的需要取模怎么办呢?
这就需要 NTT。
快速数论变换
在快速傅里叶变换中,我们使用的 \(\omega\) 是 \(n\) 次单位根 \((1,\cos(\dfrac{2\pi}{n}))\)。那么我们考虑,能不能将 \(\omega\) 换成其它数,比如说,某些整数,这样我们就能支持取模操作呢?
比如说我们要把多项式乘法放到模 \(M\) 的意义下。
那么我们应该选择怎样的 \(\omega\) 呢?
考虑在 FFT 中,我们用到了 \(\omega\) 的哪些性质:
- \(\omega_n^i=\omega_n^{i+n}\)
- \(\omega_n^i=(\omega_n^1)^i\)
- \(\omega_n^i=\omega_{n/2}^{i/2}\)
- \([i\equiv 0\pmod{n}]=\dfrac{1}{n}\sum\limits_{t=0}^{n-1}(\omega_n^{i})^t\)
当然,还有一个隐含的条件,那就是所有的 \(\omega_i\) 互不相同。
怎样构造这样的 \(\omega_i\) 呢?
看到条件 \(2\) 很容易想到 \(\omega_i=t^i\)
再看到条件 \(1\),联系费马小定理,可以想到 \(t=g^{\frac{M-1}{n}}\),这样 \(t^n=g^{M-1}\equiv 1\pmod{n}\),这样条件 \(3\) 也就满足了,因为 \(\omega_n^i=(g^{\frac{M-1}{n}})^i=(g^{2\times\frac{M-1}{n}})^{i/2}=(g^{\frac{M-1}{n/2}})^{i/2}=\omega_{n/2}^{i/2}\)。
但是这个 \(g,M\) 当然不是想取多少就取多少的,由于 \(\omega_i\) 互不相同,所以 \(g^1,g^2,\dots,g^{M-1}\) 应当互不相同,这意味着 \(g\) 应当是 \(M\) 的原根。并且由于分数出现在指数上会特别麻烦,所以 \(M-1\) 应当整除 \(n\),也就是 \(M\) 应当写成 \(c\times 2^k+1\) 的形式。我们发现,满足这样的 \(g,M\) 数量非常少。我们熟知的 \(998244353\) 就是其中一个满足条件的 \(M\),因为 \(998244353=119\times 2^{23}+1\),它对应的原根是 \(3\)。
当然还有其它容易出现的 NTT 模数,例如 \(1004535809=479\times 2^{21}+1\),它对应的原根为 \(3\);\(924844033=441\times 2^{21}+1\),它的原根是 \(5\)。
void NTT(int *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
int W=prs[i][type<0];
for(int j=0;j<len;j+=i){
int w=1;
for(int k=0;k<(i>>1);k++,w=1ll*w*W%MOD){
int X=a[j+k],Y=1ll*a[(i>>1)+j+k]*w%MOD;
a[j+k]=(X+Y)%MOD;a[(i>>1)+j+k]=(X-Y+MOD)%MOD;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i]=1ll*a[i]*inv[len]%MOD;//to avoid forgetting to divide the a[i] by N
}
然后主函数里写:
while(LEN<=n+m) LEN<<=1,LOG++;
for(int i=1;i<=LEN;i<<=1){
inv[i]=qpow(i,MOD-2);
prs[i][0]=qpow(pr,(MOD-1)/i);
prs[i][1]=qpow(ipr,(MOD-1)/i);
}
任意模数 NTT
名字听起来很吓人,其实根本不是啥高深的技巧
考虑取三个不同的模数 \(M_1,M_2,M_3\),(比如说 \(998244353,1004535809,924844033\)),三遍 NTT 求出最终每一项对 \(M_1,M_2,M_3\) 取模的结果,然后 CRT 合并即可,总共需要 9 次 DFT。
还有一种做法,就是设一个临界值 \(M\),一般取 \(31622\) 或者 \(32768\),然后将 \(a_i\) 拆分成 \(a_{0,i}\times M+a_{1,i}\),然后对 \(a_{0,i},a_{1,i}\) FFT 一下就行了。这样总共需要 7 次 DFT。
据说第二种做法可以优化到 4 次 DFT?然鹅我不会,关于 FFT 优化的事情且先不谈
例题:
俗话说:千里之行始于足下。要学好多项式,需先打好 FFT/NTT 的基础。
1. CF632E Thief in a Shop
一道 NTT/生成函数的入门题。
考虑设 \(f_i=\sum\limits_{i=1}^kx^{b_i}\)。然后 \(f^k\) 的非零项即可。
为什么?其实就是生成函数/母函数最基本的思想。我们显然可以把 \(f^k\) 看作 \(k\) 个括号连乘的形式,那么最终的结果其实是每个括号中选一个 \(x^{b_i}\) 并将指数加在一起,这也就对应着一种偷商品的方案,故最终 \(f^k\) 的第 \(x\) 项非零也就意味着偷商品总价值 \(=x\) 的方案存在。
不过听说这题 NTT 模数 \(998244353\) 和 \(1004535809\) 都被卡了?orzorz,还好没卡 \(924844033\)(
2. P3338 [ZJOI2014]力
为啥电场强度可以是负数呢?
对式子进行一番观察,在 \(E_i\) 和 \(F_j\) 的表达式中都各有一个 \(q_j\) 可以直接消去。故原题就变成了计算:
设 \(a_i=q_i,b_i=\dfrac{1}{i^2}\),那么原式就变成 \(\sum\limits_{j<i}a_jb_{i-j}+\sum\limits_{j>i}a_jb_{j-i}\)。
发现左边那玩意儿可以转化为 \(\sum\limits_{x+y=i}a_xb_y\) 的形式,可以直接卷,但右边是 \(\sum\limits_{x-y=i}a_xb_y\) 的形式,不太好直接卷。
不过我们考虑设 \(c_i=q_{n-i+1}\),那么右边的东西就是 \(\sum\limits_{j>i}c_{n-j+1}b_{j-i}\),也就是 \(\sum\limits_{x+y=n-i+1}c_xb_y\),这样就写成一个卷积的形式了。
于是我们得到了 FFT/NTT 一个很重要的技巧,看到形如 \(\sum\limits_{x-y=i}a_xb_y\) 的东西就将某个数组翻转。
3. P3723 [AH2017/HNOI2017]礼物
不难发现,将 \(b\) 数组整体加 \(c\) 等价于将 \(a\) 数组整体减 \(c\),所以我们只用枚举 \(a\) 数组的增量 \(c\in [-m,m]\) 即可。
设 \(b'_i\) 为 \(b_i\) 经过旋转后得到的数组。
那么需要的代价 \(W=\sum\limits_{i=1}^n(a_i+c-b'_i)^2=\sum\limits_{i=1}^na_i^2+c^2+b'^2_i+2ca_i-2cb_i-2a_ib'_i\)
注意到,\(\sum\limits_{i=1}^na_i,\sum\limits_{i=1}^nb'^2_i,\sum\limits_{i=1}^nc^2,\sum\limits_{i=1}^n2ca_i,\sum\limits_{i=1}^n2cb'_i\) 都是定值(不随 \(b'\) 的变化而变化),直接一遍预处理就可以 \(\mathcal O(1)\) 算得。
唯独 \(\sum\limits_{i=1}^n2a_ib'_i\) 不是定值,而它跟在一个负号之后,故我们要求它的最大值。
考虑 \(b'_i\) 是什么东西。假设我们旋转了 \(k\) 步,那么对于 \(i\leq n-k\) 有 \(b'_i=b_{i+k}\);对于 \(i>n-k\) 有 \(b'_i=b_{i-(n-k)}\),故 \(\sum\limits_{i=1}^n2a_ib'_i=\sum\limits_{i=1}^{n-k}2a_ib_{i+k}+\sum\limits_{i=n-k+1}^n2a_ib_{i-(n-k)}\)。
我们惊喜地发现,左右两部分都可以写成 \(\sum\limits_{x-y=i}f_xg_y\) 的形式。
老套路,设 \(a'_i=a_{n-i+1}\),则原式 \(=\sum\limits_{i=1}^{n-k}2a'_{n-i+1}b_{i+k}+\sum\limits_{i=n-k+1}^n2a'_{n-i+1}b_{i-(n-k)}\),预处理 \(a'\) 和 \(b\) 的卷积 \(f\) 就可以 \(\mathcal O(1)\) 对于每个 \(k\) 求出上述式子的值了,其值为 \(2(f_{n+k+1}+f_{k+1})\)。
注意到这个 \(\sum\limits_{i=1}^n2a_ib'_i\) 与 \(c\) 无关,故不用对于每个 \(c\) 都卷一遍,预处理这玩意儿的最大值,然后对于每个 \(c\) 算一遍剩余部分的值即可。
4. Atcoder Grand Contest 005F Many Easy Problems
1900 分 AGC F 神题,一看就是我不会做的亚子啊/kk
考虑对于给定的集合 \(S\) 怎样求 \(f(S)\),一个点 \(u\) 会对 \(f(S)\) 产生 \(1\) 的贡献当且仅当 \(u\in S\) 或者 \(u\) 有两个子树中包含 \(S\) 内的节点。
反过来说,一个点 \(u\) 不会对 \(f(S)\) 产生贡献当且仅当 \(S\) 中的点全在 \(u\) 的某个子树中。
假设我们规定的集合 \(S\) 的大小为 \(k\),对于某个点 \(u\),有 \(m\) 个大小分别为 \(s_1,s_2,\dots,s_m\) 的子树,那么共有 \(\dbinom{s_1}{k}+\dbinom{s_2}{k}+\dots+\dbinom{s_m}{k}\) 个集合 \(S\) 满足 \(u\) 不会对 \(f(S)\) 产生贡献。
从反面考虑,拿总贡献 \(n\times\dbinom{n}{k}\) 减去不会产生的贡献。i.e,\(ans_k=n\times\dbinom{n}{k}-\sum\limits_{u=1}^n\sum\limits_{j=1}^{m_u}\dbinom{s_{u,j}}{k}\),其中 \(m_u\) 为以 \(u\) 为根的子树个数,\(s_{u,1},s_{u,2},\dots,s_{u,m_u}\) 分别为这 \(m_u\) 个子树的大小。
显然我们并不用考虑这 \(u_m\) 个子树具体是什么,只用关心它的大小。故我们可以求出大小为 \(s\) 的子树的个数 \(c_s\),原式变为 \(ans_k=n\times\dbinom{n}{k}-\sum\limits_{s=1}^nc_s\times\dbinom{s}{k}\)。
拆组合数,得到 \(ans_k=n\times\dbinom{n}{k}-\sum\limits_{s=1}^nc_s\times\dfrac{s!}{k!(s-k)!}\)
把 \(\dfrac{1}{k!}\) 提到外面去可以得到:\(ans_k=n\times\dbinom{n}{k}-\dfrac{1}{k!}\times\sum\limits_{s=1}^nc_s\times\dfrac{s!}{(s-k)!}\)
令 \(a_i=c_i\times i!,b_i=\dfrac{1}{i!}\),那么原式变为 \(ans_k=n\times\dbinom{n}{k}-\dfrac{1}{k!}\times\sum\limits_{s=1}^na_sb_{s-k}\)
发现又是 \(\sum\limits_{x-y=i}f_xg_y\) 的形式,立马将其中某个数组翻转一下。我是令 \(b'_i=b_{n-i+1}\),求一下 \(a\) 和 \(b'\) 的卷积就行了。
还有这题模数是 \(924844033\),其原根是 \(5\)……
5. P4173 残缺的字符串
众所周知,字符串匹配有三种方式:
-
哈希
-
KMP/Z
-
FFT
今天我们来聊一聊第三种方法。
先考虑这题不带通配符的版本,也就是最经典的字符串匹配。
考虑设 \(C(x,y)\) 为字符 \(x\) 与字符 \(y\) 是否匹配,如果匹配返回 \(0\),否则返回一个非零的值。
再设 \(f_j\) 表示以 \(s_j\) 开头的长度为 \(|t|\) 的子串是否与 \(t\) 匹配,如果匹配返回 \(0\),否则返回一个非零的值。
那么 \(f_j=\sum\limits_{i=1}^{|t|}C(s_{j+i-1},t_i)\)
那么究竟取怎样的 \(C(x,y)\) 才合适呢?
一个很 naive 的想法是设 \(C(x,y)=x-y\),但这样很显然是错误的,因为这样会导致 ab 与 ba 匹配了。
回忆起初一时讲过的一个东西:若 \(a,b,c\) 为实数,\(a^2+b^2+c^2=0\) 就意味着 \(a=b=c=0\)。
于是思路就来了,设 \(C(x,y)=(x-y)^2\),这样只有当 \(s_j-t_1=0,s_{j+1}-t_2=0,s_{j+2}-t_3=0,\dots,s_{j+|t|-1}-t_{|t|}=0\) 同时满足的时候 \(f_j\) 才能等于 \(0\),符合条件。
那么怎么求 \(f_j\) 呢?
\(f_j=\sum\limits_{i=1}^{|t|}(s_{j+i-1}-t_i)^2=\sum\limits_{i=1}^{|t|}s_{j+i-1}^2+t_i^2-2s_{j+i-1}t_i\)
左边两个平方项只与 \(s\) 或者只与 \(t\) 有关,前缀和预处理后显然可以 \(\mathcal O(1)\) 地求。
而后面的交叉项又是喜闻乐见的 \(\sum\limits_{x-y=i}f_xg_y\) 的形式,把 \(t\)(或 \(s\))翻转一下预处理个卷积也可以 \(\mathcal O(1)\) 求。
时间复杂度 \(\mathcal O(n\log n)\)。
你可能会说,FFT 字符串匹配好菜啊,时间复杂度甚至不如 hash/KMP,常数还巨大,根本没有推广的必要。
如果你这样认为那你就大错特错了,碰到像 P4173 这类含通配符的字符串就只能用 FFT 了。记得去年 3 月某场 Atcoder 的 E 是含通配符的字符串匹配,结果还想着用 Z 乱搞,搞了半天发现 Z 是假的。
为什么?首先含通配符的 hash 肯定搞不定,否则请给出 hash 函数怎么求。。。
如果你要用 KMP/Z,那么你都要用到字符串匹配的一条性质:如果字符串 \(a\) 与 \(b\) 匹配,\(a\) 与 \(c\) 匹配,那么 \(b\) 与 \(c\) 一定匹配。
但这个性质换到含通配符的字符串匹配就不成立了。举个很简单的栗子,\(a="*",b="a",c="b"\)。所以含通配符的字符串匹配也不能 KMP/Z。
那就只能 FFT 了呗。
还是设 \(C(x,y)\) 为字符 \(x\) 与字符 \(y\) 是否匹配,如果匹配返回 \(0\),否则返回一个非零的值;\(f_j\) 表示以 \(s_j\) 开头的长度为 \(|t|\) 的子串是否与 \(t\) 匹配,如果匹配返回 \(0\),否则返回一个非零的值。
按照套路还是有 \(f_j=\sum\limits_{i=1}^{|t|}C(s_{j+i-1},t_i)\)。
那么这下子 \(C(x,y)\) 该设为什么东西呢?
考虑在什么情况下字符 \(x\) 与 \(y\) 能匹配,要么 \(x\) 为 \(0\),要么 \(y\) 为 \(0\),要么 \(x=y\)。
还是联想到初一数学,若 \(a,b,c\) 为实数,\(abc=0\) 就意味着 \(a=0\ \or\ b=0\ \or c=0\)。
于是思路就有了,给每个字符赋一个权值,通配符的权值为 \(0\),\(a\) 的权值为 \(1\),\(b\) 的权值为 \(2\),以此类推。
设 \(X\) 为 \(x\) 的权值,\(Y\) 为 \(y\) 的权值,那么 \(C(x,y)=XY(X-Y)^2\)。这样 \(C(x,y)=0\) 当且仅当 \(x\) 为通配符或 \(y\) 为通配符或 \(x=y\)。
最后就是求 \(f_j\) 的问题了,设 \(a_i\) 为 \(s_i\) 的权值,\(b_i\) 为 \(t_i\) 的权值,还是将平方项拆开,\(f_j=\sum\limits_{i=1}^{|t|}a_{j+i-1}b_i(a_{j+i-1}-b_i)^2=\sum\limits_{i=1}^{|t|}a_{j+i-1}^3b_i+a_{j+i-1}b_i^3-2a_{j+i-1}^2b_i^2\)
发现三项都是 \(\sum\limits_{x-y=i}f_xg_y\) 的形式,求三遍卷积就 ok 了。
不过似乎常数上天了啊……
6. CF1096G Lucky Tickets
跟 CF632E 几乎一模一样……
还是设 \(f_x=\sum\limits_{i=1}^kx^{d_i}\),快速幂求出 \(f^{n/2}\)。
还是把 \(f^{n/2}\) 看作 \(n/2\) 个括号连乘的形式,将得到的多项式看作每个括号中选一个 \(x^{b_i}\) 并将指数加在一起,第 \(i\) 个括号取了 \(x^{b_j}\) 等价于第 \(i\) 位上放 \(b_j\)。故每个和为 \(s\) 的填法都会对 \(x^s\) 产生 \(1\) 的贡献。故得到的多项式 \(x^i\) 前的系数就是前 \(n/2\) 和为 \(i\) 的方案数。
最终答案即为 \(\sum f_i^2\)
7. P5641 【CSGRound2】开拓者的卓识
一道挺有意思的题,并且竟然自己搞出来了!
首先要清楚 \(sum_{k,l,r}\) 的含义是什么。
\(sum_{1,l,r}\) 就不用多说了,就是 \(a_l\) 到 \(a_r\) 的和。
\(sum_{2,l,r}\) 根据 \(sum_{k,l,r}\) 的公式,可以看作是选择一个区间 \([l_1,r_1]\subseteq [l,r]\),再将 \(a_{l_1}\) 到 \(a_{r_1}\) 的和累加入答案中。
\(sum_{3,l,r}\) 是选择一个区间 \([l_1,r_1]\subseteq[l,r]\),再对 \([l_1,r_1]\) 求一遍 \(sum_{2,l_1,r_1}\),也就是再选择一个区间 \([l_2,r_2]\in [l_1,r_1]\) 将 \(a_{l_2}\) 到 \(a_{r_2}\) 的和加入答案中。
…………
\(sum_{k,l,r}\) 就是选择 \(k-1\) 个区间 \([l_{k-1},r_{k-1}]\subseteq [l_{k-2},r_{k-2}]\subseteq\dots\subseteq[l_1,r_1]\subseteq [l,r]\),并将 \([l_k,r_k]\) 的和加入答案中。
考虑转换贡献体,枚举 \(a_i\) 会对 \(sum_{k,1,r}\) 产生多大的贡献,也就是有多少组区间 \([l_i,r_i]\) 满足 \(i\in[l_{k-1},r_{k-1}]\subseteq [l_{k-2},r_{k-2}]\subseteq\dots\subseteq[l_1,r_1]\subseteq [1,r]\),由于是相邻区间之间是包含关系,故 \(i\geq l_{k-1}\geq l_{k-2}\geq\dots\geq l_1\geq 1\),记 \(d_k=i-l_{k-1},d_{k-1}=l_{k-1}-l_{k-2},\dots,d_2=l_2-l_1,d_1=l_1-1\),那么有 \(d_1+d_2+d_3+\dots+d_k=i-1\),其中 \(d_i\geq 0\),采用隔板法可求得所有 \((l_1,l_2,\dots,l_{k-1})\) 的个数为 \(\dbinom{i+k-2}{k-1}\)。同理可得所有 \((r_1,r_2,\dots,r_{k-1})\) 的个数为 \(\dbinom{r-i+k-1}{k-1}\)。
故 \(a_i\) 对 \(r\) 产生的贡献为 \(a_i\times \dbinom{i+k-2}{k-1}\times \dbinom{r-i+k-1}{k-1}\)。记 \(A_i=a_i\times \dbinom{i+k-2}{k-1},B_i=\dbinom{i+k-2}{k-1}\),求一遍 \(A\) 与 \(B\) 的卷积 \(C\),那么 \(C_{r+1}=sum_{k,1,r}\)。
8. P5075 [JSOI2012] 分零食
首先很容易观察到,\(A\leq 10^8\) 的数据范围其实是假的,\(A>M\) 和 \(A=M\) 的答案其实是一样的,因为最多只有 \(M\) 个人才能拿到糖,其它 \(A-M\) 个人都是来打酱油,撑场子的。
考虑暴力 \(dp\),\(dp_{i,j}=\) 前 \(i\) 个人中共拿了 \(j\) 个糖的欢乐程度的乘积之和,那么 \(dp_{i,j}=\sum\limits_{k=1}^jdp_{i-1,j-k}\times f(k)\),其中 \(f(i)=Oi^2+Si+U\),最终答案即为 \(\sum\limits_{i=1}^Adp_{i,M}\)。时间复杂度 \(m^3\),期望得分 40。
发现上述式子可以写成卷积的形式,故可以使用 FFT 优化,时间复杂度 \(m^2\log m\),期望得分 60。
注意到我们复杂度的瓶颈在于,我们每做一次卷积都要将答案加入贡献。如果最终答案仅仅只是 \(dp_{A,M}\) 那显然多项式快速幂就行了。
故我们考虑记 \(g_{i,j}=\sum\limits_{k=1}^idp_{k,j}\),最终答案即为 \(g_{A,M}\)。
考虑怎么算 \(g_i\):
- 如果 \(i\) 为奇数,那么 \(g_{i}=g_{i-1}+dp_{i}\)。
- 如果 \(i\) 为偶数,那么 \(g_i=g_{i/2}+dp_{i/2}\times g_{i/2}\)
多项式快速幂即可。
至于这个模数 \(P\) 如何处理,其实不用任意模数 NTT,注意到这个 \(P\) 很小,所以暴力 FFT 也不会爆精度。
时间复杂度 \(m\log^2m\)。
9. P5488 差分与前缀和
你可能会好奇,前缀和/差分跟多项式有关系吗?
你可别说,还真有。
对于前缀和数组 \(s_i=\sum\limits_{j=1}^ia_j\),如果我们把它看作卷积的形式 \(s_i=\sum\limits_{j=0}^ia_{i-j}b_j\)
那么就有 \(s_i=\sum\limits_{i=0}^ia_{i-j}\times 1\)。
也就是说,\(s\) 是 \(a\) 与一个全 \(1\) 的多项式的乘积。
故 \(a_i\) 的 \(k\) 阶前缀和可以表示为 \(a\times (1+x+x^2+x^3+\dots)^k\)
考虑后面那个多项式是什么东西,考察 \(x^s\) 前的系数。我们还是采用这个取括号的思想,假设第 \(i\) 个括号选了 \(x^{b_i}\),那么有 \(b_1+b_2+b_3+\dots+b_k=s\),\(x^s\) 前的系数就是该方程满足 \(b_i\geq 0\) 的解的个数。使用隔板法易算出答案为 \(\dbinom{s+k-1}{k-1}\),将这两个多项式求个卷积就行了。
接下来考虑差分数组 \(d_i=a_i-a_{i-1}\),借鉴刚刚的思想可知 \(d\) 是 \(a\) 与多项式 \(1-x\) 的卷积。
故 \(a_i\) 的 \(k\) 阶差分可以表示为 \(a\times (1-x)^k\),将后面的多项式用二项式定理拆开得到 \((1-x)_i^k=(-1)^i\times \dbinom{k}{i}\),还是将两个多项式求个卷积就行了。
10. CF993E Nikita and Order Statistics
我们把 \(<x\) 的数设为 \(1\),\(\geq x\) 的数设为 \(0\),并该数组求一遍前缀和。那么区间 \([l,r]\) 中有 \(k\) 个 \(<x\) 的数等价于 \(s_r-s_{l-1}=k\)。
故含 \(k\) 个 \(<x\) 的数的区间个数就是满足 \(s_r-s_{l-1}=k\) 的 \([l,r]\) 的个数。
稍微移个项可得 \(s_r=s_{l-1}+k\)。
设 \(c_x\) 表示有多少个 \(s_i=x\),那么 \(ans_k=\sum\limits_{i=0}^{n-k}c_ic_{i+k}\)
又是喜闻乐见的 \(\sum\limits_{x-y=i}f_xg_y\) 的形式,直接把某个数组翻转一下跑遍 FFT 就行了。
11. P4199 万径人踪灭
首先肯定要枚举对称轴,假设我们以 \(x\) 为对称轴(若 \(x=k\)(\(k\) 为整数)则关于第 \(k\) 个字符对称,若 \(x=k+0.5\),则关于第 \(k\) 个与第 \(k+1\) 个字符间的缝隙对称)
设 \(cnt\) 为满足 \(i<j,a_i=a_j\) 并且 \(i,j\) 关于 \(x\) 对称的 \((i,j)\) 的个数。
那么对于这 \(cnt\) 个 \((i,j)\),\(a_i\) 与 \(a_j\) 要么同时选,要么同时不选,共 \(2^{cnt}\) 种方案,扣掉空集,共 \(2^{cnt}-1\) 种。对于所有这样的 \(x\) 把对应的 \(2^{cnt}-1\) 加起来就行了。
那么怎么求这个 \(cnt\) 呢?显然 \(i,j\) 关于 \(x\) 当且仅当 \(i+j=2x\)。我们记字符 a 为 \(0\),字符 \(b\) 为 \(1\)。于是 \(cnt_{x}=\sum\limits_{i+j=2x}(1-a_i-a_j)^2\)。随便卷一下就行了。
但题目中还说“位置不能连续”,这意味着所有连续的回文子串不符合题意,故要扣掉连续的回文子串的个数。
怎样求连续的回文子串的个数呢?manacher 一下,然后把所有的 \(len_i-1\) 加起来就好了。
12. CF528D Fuzzy Search
记 \(p(i,c)\) 表示位置 \(i\) 上放上字符 \(c\) 是否合法。\(p(i,c)=1\) 当且仅当存在 \(s_j=c\) 且 \(|i-j|\leq k\)。
求 \(p(i,c)\) 非常容易,对于 \(s_i=c\) 将 \(p(i-k,c),p(i-k+1,c),\dots,p(i+k-1,c),p(i+k,c)\) 都设为 \(1\),直接差分一下就行了。
再设 \(f_i\) 表示以 \(i\) 开头的长度为 \(|t|\) 字符串能与 \(t\) 成功匹配多少位。显然 \(f_i=\sum\limits_{j=1}^{|t|}p(i+j-1,t_j)\)。
发现不太好直接卷,我们不妨做一个转化。枚举每个字符 \(c\in\{\texttt{ACTG}\}\),设 \(b_j\) 表示 \(t_j\) 是否等于 \(c\)。那么字符 \(c\) 给 \(f_i\) 带来的贡献就是 \(\sum\limits_{j=1}^{|t|}p(i+j-1,c)\times b_j\)。再设 \(a_i=p_{i,c}\),那么原式就变成了我们最爱的形式——\(\sum\limits_{x-y=i}f_xb_y\)。把某个串翻转一下跑遍 FFT 就好了。
13. CF954I Yet Another String Matching Problem
考虑暴力匹配两个字符串 \(s,t\) 是怎样的过程:对于每个 \(i\),我们在 \(s_i\) 与 \(t_i\) 之间连一条边,表示 \(s_i\) 需要变到 \(t_i\)。
然后对于建好的图中的每个连通块,显然我们都可以并且必须选择某个点并将连通块中其余的点全部变成这个值。这样需要 \(\text{连通块大小}-1\) 次操作。故从 \(s\) 到 \(t\) 的最小操作次数就是 \(\sum\text{连通块大小}-1\)。
于是本题思路就来了,设 \(f_{i,c1,c2}\) 表示,对于 \(s\) 中以 \(i\) 开头的长度为 \(|t|\) 的子串 \(s'\),满足 \(s'_i=c1,t_i=c2\) 的 \(i\) 的个数。
怎样求 \(f_{i,c1,c2}\)?这又回到了我们前几题的套路,令 \(a_i\) 表示 \(s_i\) 是否等于 \(c1\),\(b_i\) 表示 \(t_i\) 是否等于 \(c2\)。故 \(f_{i,c1,c2}=\sum\limits_{j=0}^{|t|}a_{i+j-1}b_j\),把 \(b\) 翻转一下求个卷积就行了。
然后对于每个 \(i\),枚举 \(f_{i,c1,c2}>0\) 的 \(c1,c2\),然后跑上述操作即可。
时间复杂度 \(\mathcal O(6^2n\log n)\),虽然可以过,但是显然常数上天了。这个做法需要跑 \(3\times 6^2=108\) 次 DFT+IDFT。不过我们发现,可能的 \(a,b\) 最多只有 \(6\) 种,所以可以对每个 \(c1\) 单独求一遍 \(a_i\),并对这个 \(a_i\) 跑一遍 DFT。\(b_i\) 也是如此。这样共需 \(6\times 2=12\) 次 DFT 和 \(6^2=36\) 次 IDFT。还有一个小优化,就是对于 \(c1=c2\),\(f_{i,c1,c2}\) 显然不会对答案产生任何影响,这样可以再少跑 \(6\) 次 IDFT,这样就只用跑 \(42\) 次 DFT+IDFT 了。
还有为啥这题 difficulty 才 2200 啊,与它难度相当的 CF1334G 都有 2900 了。
14. CF1334G Substring Search
2900 的题来了
还是借鉴 P4173 残缺的字符串的思想,设 \(C(x,y)\) 为字符 \(x\) 与字符 \(y\) 是否匹配,如果匹配返回 \(0\),否则返回一个非零的值。
再设 \(f_j\) 表示以 \(s_j\) 开头的长度为 \(|t|\) 的子串是否与 \(t\) 匹配,如果匹配返回 \(0\),否则返回一个非零的值。
那么 \(f_j=\sum\limits_{i=1}^{|t|}C(s_{j+i-1},t_i)\)
关键还是在于 \(C(x,y)\) 上。\(C(x,y)=0\) 当且仅当 \(y=x\) 或 \(y=p_x\)。还是借鉴初一数学的思想,若 \(a,b\) 为实数,\(ab=0\) 就意味着 \(a=0\ \or\ b=0\)。
故我们有 \(C(x,y)=(x-y)^2(p_x-y)^2\)。
于是 \(f_j=\sum\limits_{i=1}^{|t|}(s_{j+i-1}-t_i)^2(p_{s_{j+i-1}}-t_i)^2\)
把它拆开并以 \(t_i\) 为主元合并,可以得到 \(t_i^0,t_i^1,t_i^2,t_i^3,t_i^4\) 项,对于 \(t_i^0\) 和 \(t_i^4\) 项暴力求个前缀和可以搞定,对于另外三项各跑一遍 FFT 就可以得到对应的结果。把这五项的结果加起来就可以得到 \(f_i\) 的值。
15. P3702 [SDOI2017]序列计数
显然,答案可以通过总方案减去不包含质数的方案数。这里以计算总方案数为例。
记 \(c_i\) 表示在 \(1\) 到 \(m\) 中模 \(p\) 余 \(i\) 的个数。
那么有一个显然的 \(dp\),设 \(dp_{i,j}\) 表示在前 \(i\) 个数中,前 \(i\) 个数的和模 \(p\) 余 \(j\) 的方案数。
转移也非常显然,\(dp_{i+1,(j+k)\bmod p}+=dp_{i,j}\times c_j\)
这玩意儿显然可以用多项式快速幂优化。
另外这题模数相当恶心,还要写一遍任意模数 NTT(其实暴力多项式乘法都没问题,不过为了加强对板子的熟练程度,还是手写了一遍任意模数 NTT)
16. P4091 [HEOI2016/TJOI2016]求和
这题我竟然自己推出来了!incredible!
首先你要了解 \(S(n,k)\) 的含义,\(S(n,k)\),即第二类斯特林数,表示将 \(n\) 个不同的球放入 \(k\) 个相同的盒子中,且不允许有空盒的方案数。
那么 \(S(n,k)\) 有递推式 \(S(n,k)=S(n-1,k-1)+S(n-1,k)\times k\)。考虑最后一个球怎么放。如果它单独放在一个盒子中,那么方案数就是 \(S(n-1,k-1)\),如果它与其它某些球放在同一个盒子中,那么相当于将 \(n-1\) 个球放入 \(k\) 个盒子中,方案数为 \(S(n-1,k)\times k\),将二者一加即可得到第二类 stirling 数的递推式。
\(S(n,k)\) 的通项公式:\(S(n,k)=\dfrac{1}{k!}\sum\limits_{i=0}^ki^n\times\dbinom{k}{i}\times(-1)^{k-i}\)。
考虑怎样证明这个公式:
令 \(b_k=k^n=\sum\limits_{i=0}^k\dbinom{k}{i}\times S(n,i)\times i!\),即将 \(n\) 个球放入 \(k\) 个不同的盒子,对是否有空盒也不做要求的方案数,显然 \(b_k\) 就是 \(k^n\),即每个球都随便放入一个盒子的方案数乘在一起。
而 \(b_k=\sum\limits_{i=0}^k\dbinom{k}{i}\times (-1)^i\times S(n,i)\times i!\times (-1)^i\)(将 \(1\) 拆成 \((-1)^i\times (-1)^i\))
再令 \(a_k=S(n,k)\times k!\times (-1)^k\)。
由二项式反演可得:
\(\because b_k=\sum\limits_{i=0}^k(-1)^i\dbinom{k}{i}a_i\)
\(\therefore a_k=\sum\limits_{i=0}^k(-1)^i\dbinom{k}{i}b_i\)
即 \(S(n,k)\times k!\times (-1)^k=\sum\limits_{i=0}^k(-1)^i\dbinom{k}{i}i^n\)
故 \(S(n,k)=\dfrac{1}{k!}\sum\limits_{i=0}^ki^n\times\dbinom{k}{i}\times(-1)^{k-i}\)
知道了这个公式之后,把它代入题目要求的式子,可得
\(ans=\sum\limits_{i=0}^n\sum\limits_{j=0}^i2^j\times j!\times \dfrac{1}{j!}\sum\limits_{k=0}^jk^i\times\dbinom{j}{k}\times (-1)^{j-k}\)
由于当 \(j>i\) 时 \(S(i,j)=0\),故 \(\sum\limits_{j=0}^i\) 可直接改为 \(\sum\limits_{j=0}^n\),进而又可以得到:
\(ans=\sum\limits_{i=0}^n\sum\limits_{j=0}^n2^j\sum\limits_{k=0}^jk^i\times\dbinom{j}{k}\times (-1)^{j-k}\)
拆组合数可得:
\(ans=\sum\limits_{i=0}^n\sum\limits_{j=0}^n2^j\sum\limits_{k=0}^jk^i\times\dfrac{j!}{k!(j-k)!}\times (-1)^{j-k}\)
我们发现这里的 \(i\) 只在 \(k^i\) 中出现过,故转化枚举顺序,先枚举 \(j,k\) 再枚举 \(i\):
\(ans=\sum\limits_{j=0}^n2^j\sum\limits_{k=0}^j(\sum\limits_{i=0}^nk^i)\times\dfrac{j!}{k!(j-k)!}\times (-1)^{j-k}\)
显然 \((\sum\limits_{i=0}^nk^i)\) 可以用等比数列求和公式 \(\mathcal O(\log n)\) 地算出,记其为 \(c_k\)。
\(ans=\sum\limits_{j=0}^n2^j\sum\limits_{k=0}^jc_k\times\dfrac{j!}{k!(j-k)!}\times (-1)^{j-k}\)
看到了我们很喜欢的 \(k\) 与 \(j-k\),故考虑将带 \(k\) 的合并,带 \(j-k\) 的合并,与 \(k\) 无关的丢到外面,又可以得到:
\(ans=\sum\limits_{j=0}^n2^j\times j!\times\sum\limits_{k=0}^j(c_k\times\dfrac{1}{k!})\times (\dfrac{1}{(j-k)!}\times(-1)^{j-k})\)
令 \(a_k=c_k\times\dfrac{1}{k!},b_k=\dfrac{1}{k!}\times (-1)^k\),则
\(ans=\sum\limits_{j=0}^n2^j\times j!\times\sum\limits_{k=0}^ja_kb_{j-k}\)
是不是感觉后面那俩玩意儿可以卷?对 \(a\) 和 \(b\) 求个多项式卷积 \(h\),然后 \(ans=\sum\limits_{j=0}^n2^j\times j!\times h_j\)。
然后这题就做完了。
注意,当 \(k=0,1\) 时候 \(c_k\) 需进行特判。显然 \(c_1=n+1\),但是 \(c_0\) 的值需要特别注意。我一直把它当 \(0\) 算,结果就总 WA。其实你代入特殊值 \(n=0\) 可手算得 \(ans=1\),而将 \(n=0\) 代入上式可得 \(ans=c_0\),故 \(c_0=1\)。
u1s1 这题是我在医院做的哦
17. P3321 [SDOI2015]序列统计
刚看到这题,是否觉得很熟悉?
如果把“所有数的乘积 \(\bmod m=x\)”改为“所有数的和 \(\bmod m=x\)”,那显然就是前不久我们刚做过的 P3702 [SDOI2017]序列计数。
那么有什么操作能够变乘为加呢?
立马想到取对数运算。
可是,我们说,取对数运算 \(\log_ab\) 是一个在实数范围内定义的函数,怎么放到模意义下呢?
考虑模运算的逆运算,也就是指数运算。我们随便令一个数 \(a\) 为底,然后对于 \(i\in [0,m-2]\),令 \(log[a^i\bmod m]=i\) 即可。
但是这个底数 \(a\) 真 的 可 以 随 便 取 吗?
譬如我们取 \(a=4,m=17\),那么我们有 \(a^0\equiv a^4\equiv a^8\equiv a^{12}\equiv 1\pmod{m}\)。
故我们取的 \(a\) 必须满足 \(a^0,a^1,\dots,a^{m-2}\) 模 \(m\) 的余数各不相同。
看到这个条件,我们就可以想到原根。
由于 \(m\) 为质数,所以 \(m\) 一定有原根。
暴力求出 \(m\) 的原根 \(a\),然后求出 \(\log_a(1),\log_a(2),\dots,\log_a(m-1)\)
最后跑遍 P3702 [SDOI2017]序列计数 就好了
18. CF1251F Red-White Fence
考虑这个奇怪的东西的周长是什么玩意儿,通过小学教的平移法可以求出 \(C=(\text{红色木板的长度}+\text{选用的木板个数})\times 2\)。
看到 \(k\) 这么小,那肯定要枚举选择哪个红色木板,这样也可以唯一确定选用的木板的个数。
于是考虑状态 \(dp_{i,j}\) 表示选择的红色木板编号为 \(i\),选择 \(j\) 个木板的方案数。
那么怎样求 \(dp_{i,j}\) 呢?
首先肯定要明确的一点是,同一种长度的白色木板顶多出现 \(2\) 次。
考虑枚举白色木板的长度,再设 \(f_{i,j}\) 表示对于长度 \(\leq i\) 的木板,选择了 \(j\) 个的方案数。
分情况讨论:
-
若没有长度为 \(i\) 的白色木板,那显然 \(f_{i,j}=f_{i-1,j}\)
-
若只有 \(1\) 个长度为 \(i\) 的木板,那 \(f_{i,j}=f_{i-1,j}+2f_{i-1,j-1}\),\(f_{i-1,j}\) 表示不选这个长度为 \(i\) 的木板,\(2f_{i-1,j-1}\) 表示选择长度为 \(i\) 的木板,而它有放在红色木板左边和右边两种选择,故要乘个 \(2\)。
-
若有 \(2\) 个(或更多)长度为 \(i\) 的木板,那 \(f_{i,j}=f_{i-1,j}+2f_{i-1,j-1}+f_{i-1,j-2}\),\(f_{i-1,j}\) 表示不选这个长度为 \(i\) 的木板,\(2f_{i-1,j-1}\) 表示选择一个长度为 \(i\) 的木板,而它有放在红色木板左边和右边两种选择,故要乘个 \(2\),\(f_{i-1,j-2}\) 表示选择两个长度为 \(i\) 的木板,显然它们只能一左一右地放,故只有 \(1\) 种选择。
通过上面的分析,不难看出情况 \(1\) 相当于啥也没干,情况 \(2\) 相当于将多项式 \(f\) 与 \(2x+1\) 求一个卷积,情况 \(3\) 相当于将多项式 \(f\) 与 \(x^2+2x+1\) 求个卷积。
设 \(c_i\) 表示有多少个长度为 \(i\) 的木板,故我们只用求出 \(c_i=1\) 和 \(c_i\geq 2\) 的 \(i\) 的个数,将其假设为 \(x_1,x_2\)。
那么最终的 \(f\) 就是 \((2x+1)^{x_1}\times (x^2+2x+1)^{x_2}\),稍微求个卷积即可。
到此为止,我们花了整整一周的时间给多项式入了个门。
惊不惊喜?意不意外?
后面还有更多更神奇的操作待学习呢。
先给出一些说明:
本篇博客里的多项式是广义上的多项式,形式幂级数,例如 \(\sum\limits_i\dfrac{x^i}{i!}\) 也可以算是多项式。
分治 FFT
19. P4721 【模板】分治 FFT
其实还蛮简单的
考虑分治地解决这个问题,用类似于 CDQ 分治的考虑左半边的 \(f\) 值对右半边的贡献。
假设我们在分治区间 \([l,r]\),我们考虑左半区间 \([l,mid]\) 对右半区间 \([mid+1,r]\) 的贡献。
根据递推式有 \(f_j=\sum\limits_{i=l}^{mid}f_ig_{j-i}\)。令 \(a_i=f_{i+l}\),则 \(f_j=\sum\limits_{i=l}^{mid}a_{i-l}g_{j-i}\),卷积一下就行了。
时间复杂度 \(n\log^2n\)。
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int pr=3;
const int MAXP=1<<18;
const int MOD=998244353;
int qpow(int x,int e){int ret=1;for(;e;e>>=1,x=1ll*x*x%MOD) if(e&1) ret=1ll*ret*x%MOD;return ret;}
int n,f[MAXP+5],g[MAXP+5];
int LEN=1,LOG=0,A[MAXP+5],B[MAXP+5],C[MAXP+5],inv[MAXP+5],prs[MAXP+5][2],rev[MAXP+5],ipr;
void NTT(int *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
int W=prs[i][type<0];
for(int j=0;j<len;j+=i){
int w=1;
for(int k=0;k<(i>>1);k++,w=1ll*w*W%MOD){
int X=a[j+k],Y=1ll*a[(i>>1)+j+k]*w%MOD;
a[j+k]=(X+Y)%MOD;a[(i>>1)+j+k]=(X-Y+MOD)%MOD;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i]=1ll*a[i]*inv[len]%MOD;
}
void solve(int l,int r){
if(l==r) return;
int mid=(l+r)>>1;solve(l,mid);
for(int i=0;i<r-l+1;i++) A[i]=B[i]=C[i]=0;
for(int i=l;i<=mid;i++) A[i-l]=f[i];
for(int i=1;i<r-l+1;i++) B[i]=g[i];
NTT(A,r-l+1,1);NTT(B,r-l+1,1);
for(int i=0;i<r-l+1;i++) C[i]=1ll*A[i]*B[i]%MOD;
NTT(C,r-l+1,-1);
for(int i=mid+1;i<=r;i++) f[i]=(f[i]+C[i-l])%MOD;
solve(mid+1,r);
}
int main(){
scanf("%d",&n);ipr=qpow(pr,MOD-2);
while(LEN<=n) LEN<<=1,LOG++;
for(int i=1;i<=LEN;i<<=1){
inv[i]=qpow(i,MOD-2);
prs[i][0]=qpow(pr,(MOD-1)/i);
prs[i][1]=qpow(ipr,(MOD-1)/i);
}
for(int i=1;i<n;i++) scanf("%d",&g[i]);
f[0]=1;solve(0,LEN-1);
for(int i=0;i<n;i++) printf("%d%c",f[i],(i==n-1)?'\n':' ');
return 0;
}
当然还有复杂度更优的多项式求逆的做法。
观察一下 \(f\) 的递推式,发现后面那东西就是 \(f\) 与 \(g\) 的卷积。
那么就可以推出 \(F(x)=F(x)G(x)\) 吗?非也。
注意到 \(F(x)G(x)\) 的常数项等于 \(f(0)g(0)=0\),而 \(f(0)=1\),故 \(F(x)=F(x)G(x)+1\)
那么这下怎么求 \(G(x)\) 呢?将原式稍微变个形即可得到 \(F(x)(1-G(x))=1\)。
由于我们要求 \(G(x)\) 的前 \(n\) 项所以这些操作都可以放在 \(\bmod x^n\) 下进行,故 \(F(x)(1-G(x))\equiv 1\pmod{x^n}\)
直接多项式求逆即可。
不过话说回来,分治 FFT 的板子干嘛要用多项式求逆呢?
不过网络流 24 题也不全是 wll 啊
多项式求逆
20. P4238 【模板】多项式乘法逆
其实也蛮简单的,一节 yyq 的课就把它推出来了。
u1s1 今年上 yyq 的课都是在颓 OI。
考虑倍增,假设我们已经知道了 \(F(x)G_0(x)\equiv 1\pmod{x^{n/2}}\),要求满足 \(F(x)G(x)\equiv 1\pmod{x^n}\) 的 \(G(x)\)
两式相减即有 \(F(x)(G(x)-G_0(x))\equiv 0\pmod{x^{n/2}}\)
由于 \(F(x)\) 有逆元,故 \(G(x)-G_0(x)\equiv 0\pmod{x^{n/2}}\)
两边平方即有 \((G(x)-G_0(x))^2\equiv 0\pmod{x^n}\)
展开可得 \(G^2(x)-2G(x)G_0(x)+G_0^2(x)\equiv 0\pmod{x^n}\)
两边同乘 \(F(x)\) 即有 \(G(x)-2G_0(x)+F(x)G^2_0(x)\equiv 0\pmod{x^n}\)
即 \(G(x)\equiv 2G_0(x)-F(x)G_0^2(x)\pmod{x^n}\)
边界条件当 \(n=1\) 的时候 \(G(x)=F(0)^{-1}\)。
NTT 求后面那玩意儿的卷积即可。
复杂度 \(T(n)=T(n/2)+n\log n\),根据主定理,这玩意儿是 \(n\log n\) 的。
为什么它是 \(n\log n\) 的呢?我还花了一中午的时间证了一遍。设 \(n=2^k\),则 \(T(n)=\sum\limits_{i=0}^k2^ii<\sum\limits_{i=0}^k2^ik=k\times(2^{k+1}-1)\),它是 \(n\log n\) 级别的。
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int pr=3;
const int MAXN=1e5;
const int MAXP=1<<18;
const int MOD=998244353;
int qpow(int x,int e){int ret=1;for(;e;e>>=1,x=1ll*x*x%MOD) if(e&1) ret=1ll*ret*x%MOD;return ret;}
int n,a[MAXP+5],b[MAXP+5];
int LEN=1,LOG=0,A[MAXP+5],B[MAXP+5],C[MAXP+5],ipr,inv[MAXP+5],rev[MAXP+5],prs[MAXP+5][2];
void NTT(int *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
int W=prs[i][type<0];
for(int j=0;j<len;j+=i){
int w=1;
for(int k=0;k<(i>>1);k++,w=1ll*w*W%MOD){
int X=a[j+k],Y=1ll*a[(i>>1)+j+k]*w%MOD;
a[j+k]=(X+Y)%MOD;a[(i>>1)+j+k]=(X-Y+MOD)%MOD;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i]=1ll*a[i]*inv[len]%MOD;
}
int main(){
scanf("%d",&n);ipr=qpow(pr,MOD-2);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
b[0]=qpow(a[0],MOD-2);
while(LEN<=n+n) LEN<<=1,LOG++;
for(int i=1;i<=LEN;i<<=1){
inv[i]=qpow(i,MOD-2);
prs[i][0]=qpow(pr,(MOD-1)/i);
prs[i][1]=qpow(ipr,(MOD-1)/i);
}
for(int i=2;i<LEN;i<<=1){
for(int j=0;j<(i<<1);j++) A[j]=B[j]=C[j]=0;
for(int j=0;j<i;j++) A[j]=a[j];
for(int j=0;j<(i>>1);j++) B[j]=b[j];
// printf("A: ");for(int j=0;j<(i<<1);j++) printf("%d%c",A[j],(j==(i<<1)-1)?'\n':' ');
// printf("B: ");for(int j=0;j<(i<<1);j++) printf("%d%c",B[j],(j==(i<<1)-1)?'\n':' ');
NTT(A,i<<1,1);NTT(B,i<<1,1);
for(int j=0;j<(i<<1);j++) C[j]=1ll*A[j]*B[j]%MOD*B[j]%MOD;
NTT(C,i<<1,-1);
// printf("C: ");for(int j=0;j<(i<<1);j++) printf("%d%c",C[j],(j==(i<<1)-1)?'\n':' ');
for(int j=0;j<i;j++) b[j]=(2*b[j]%MOD-C[j]+MOD)%MOD;
}
for(int i=0;i<n;i++) printf("%d%c",b[i],(i==n-1)?'\n':' ');
return 0;
}
多项式开根
21. P5205 【模板】多项式开根
有了多项式求逆做铺垫,多项式 sqrt 应该很水了。
同样还是一节 yyq 的课推出来的。
还是考虑倍增,假设我们已经知道 \(G^2_0(x)\equiv F(x)\pmod{x^{n/2}}\),要求满足 \(G^2(x)\equiv F(x)\pmod{x^n}\) 的 \(G(x)\)
还是考虑做差,\(G^2_0(x)-G^2(x)\equiv 0\pmod{x^{n/2}}\),\((G_0(x)+G(x))(G_0(x)-G(x))\equiv 0\pmod{x^{n/2}}\)。
由于我们要找常数项最小的 \(G(x)\),故 \(G(x)\) 和 \(G_0(x)\) 常数项均为 \(1\),此时 \(G_0(x)+G(x)\neq0\),故 \(G_0(x)-G(x)\equiv 0\pmod{x^{n/2}}\)
还是两边平方,\((G(x)-G_0(x))^2\equiv 0\pmod{x^n}\)
还是展开,\(G^2(x)-2G(x)G_0(x)+G_0^2(x)\equiv 0\pmod{x^n}\)
即 \(F(x)-2G(x)G_0(x)+G^2_0(x)\equiv 0\pmod{x^n}\)
即 \(G(x)\equiv\dfrac{F(x)+G^2_0(x)}{2G_0(x)}\pmod{x^n}\)
写个卷积函数,写个求逆函数即可实现 \(n\log n\) 求出 \(G(x)\)。
边界条件当 \(n=1\) 的时候 \(G(x)=1\)。
根据主定理时间复杂度还是 \(n\log n\)。
当然此题还有 \(f_0\neq 1\) 的版本 P5277 【模板】多项式开根(加强版),然鹅我不会二次剩余就鸽掉了。
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int pr=3;
const int MAXP=1<<18;
const int MOD=998244353;
const int INV2=499122177;
int qpow(int x,int e){int ret=1;for(;e;e>>=1,x=1ll*x*x%MOD) if(e&1) ret=1ll*ret*x%MOD;return ret;}
int n,a[MAXP+5],b[MAXP+5];
int A[MAXP+5],B[MAXP+5],C[MAXP+5],D[MAXP+5],E[MAXP+5],F[MAXP+5];
int LEN=1,LOG=0,rev[MAXP+5],inv[MAXP+5],prs[MAXP+5][2],ipr;
void NTT(int *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
int W=prs[i][type<0];
for(int j=0;j<len;j+=i){
int w=1;
for(int k=0;k<(i>>1);k++,w=1ll*w*W%MOD){
int X=a[j+k],Y=1ll*w*a[(i>>1)+j+k]%MOD;
a[j+k]=(X+Y)%MOD;a[(i>>1)+j+k]=(X-Y+MOD)%MOD;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i]=1ll*a[i]*inv[len]%MOD;
}
void polymul(int *a,int *b,int *c,int len){
for(int i=0;i<len;i++) A[i]=B[i]=0;
for(int i=0;i<len;i++) A[i]=a[i],B[i]=b[i];
NTT(A,len,1);NTT(B,len,1);
for(int i=0;i<len;i++) c[i]=1ll*A[i]*B[i]%MOD;
NTT(c,len,-1);
}
void getinv(int *a,int *b,int len){
for(int i=0;i<len;i++) b[i]=0;
b[0]=qpow(a[0],MOD-2);
for(int i=2;i<=len;i<<=1){
for(int j=0;j<(i<<1);j++) C[j]=D[j]=0;
for(int j=0;j<i;j++) C[j]=a[j];
for(int j=0;j<(i>>1);j++) D[j]=b[j];
polymul(D,D,D,i);polymul(C,D,C,i<<1);
for(int j=0;j<i;j++) b[j]=(2*b[j]%MOD-C[j]+MOD)%MOD;
}
}
void getsqrt(int *a,int *b,int len){
b[0]=1;
for(int i=2;i<=len;i<<=1){
for(int j=0;j<(i<<1);j++) E[j]=F[j]=0;
for(int j=0;j<(i>>1);j++) E[j]=b[j];
polymul(E,E,E,i);
// printf("E: ");for(int j=0;j<i;j++) printf("%d%c",E[j],(j==i-1)?'\n':' ');
for(int j=0;j<i;j++) E[j]=(E[j]+a[j])%MOD;
// printf("E: ");for(int j=0;j<i;j++) printf("%d%c",E[j],(j==i-1)?'\n':' ');
getinv(b,F,i);
// printf("F: ");for(int j=0;j<i;j++) printf("%d%c",F[j],(j==i-1)?'\n':' ');
polymul(E,F,E,i<<1);
for(int j=0;j<i;j++) b[j]=1ll*E[j]*INV2%MOD;
}
}
int main(){
scanf("%d",&n);ipr=qpow(pr,MOD-2);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
while(LEN<=n) LEN<<=1,LOG++;
for(int i=1;i<=(LEN<<1);i<<=1){
inv[i]=qpow(i,MOD-2);
prs[i][0]=qpow(pr,(MOD-1)/i);
prs[i][1]=qpow(ipr,(MOD-1)/i);
} getsqrt(a,b,LEN);
for(int i=0;i<n;i++) printf("%d%c",b[i],(i==n-1)?'\n':' ');
return 0;
}
多项式 ln
22. P4725 【模板】多项式对数函数(多项式 ln)
首先你要会求导和积分里面几个比较重要的式子。
求导:
若 \(f(x)=a_0+a_1x+a_2x^2+\dots+a_nx^n\),则 \(f'(x)=a_1+2a_2x+3a_3x^2+\dots+na_nx^{n-1}\)
若 \(f(x)=\ln x\),则 \(f'(x)=\dfrac{1}{x}\)
若 \(f(x)=e^x\),则 \(f'(x)=e^x\)
积分:
若 \(f(x)=a_0+a_1x+a_2x^2+\dots+a_nx^n\),则 \(\int f(x)=C+a_0x+\dfrac{a_1}{2}x^2+\dfrac{a_2}{3}x^3\dots+\dfrac{a_n}{n+1}x^{n+1}\),其中 \(C\) 一般等于 \(0\)。
若 \(f(x)=e^x\),则 \(\int f(x)=e^x+C\)。
回到本题来,我们要求满足 \(G(x)\equiv\ln(F(x))\pmod{x^n}\) 的 \(G(x)\)
两边同时求导可得 \(G'(x)\equiv\dfrac{F'(x)}{F(x)}\pmod{x^n}\)
后面那东西显然可以用多项式求逆+多项式卷积算出。
然后再积回去 \(G(x)=\int\dfrac{F'(x)}{F(x)}\)
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int pr=3;
const int MOD=998244353;
const int MAXP=1<<18;
int qpow(int x,int e){int ret=1;for(;e;e>>=1,x=1ll*x*x%MOD) if(e&1) ret=1ll*ret*x%MOD;return ret;}
int n,f[MAXP+5],g[MAXP+5],h[MAXP+5],A[MAXP+5],B[MAXP+5],C[MAXP+5],D[MAXP+5],E[MAXP+5];
int LEN=1,LOG=0,prs[MAXP+5][2],rev[MAXP+5],inv[MAXP+5],ipr;
void diff(int *a,int *b,int len){
for(int i=1;i<len;i++) b[i-1]=1ll*a[i]*i%MOD;
}
void integrate(int *a,int *b,int len){
for(int i=0;i<len;i++) b[i+1]=1ll*a[i]*inv[i+1]%MOD;
}
void NTT(int *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
int W=prs[i][type<0];
for(int j=0;j<len;j+=i){
int w=1;
for(int k=0;k<(i>>1);k++,w=1ll*w*W%MOD){
int X=a[j+k],Y=1ll*a[(i>>1)+j+k]*w%MOD;
a[j+k]=(X+Y)%MOD;a[(i>>1)+j+k]=(X-Y+MOD)%MOD;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i]=1ll*a[i]*inv[len]%MOD;
}
void getinv(int *a,int *b,int len){
b[0]=qpow(a[0],MOD-2);
for(int i=2;i<=len;i<<=1){
for(int j=0;j<(i<<1);j++) C[j]=D[j]=E[j]=0;
for(int j=0;j<i;j++) C[j]=a[j];
for(int j=0;j<(i>>1);j++) D[j]=b[j];
// printf("C: ");for(int j=0;j<i;j++) printf("%d%c",C[j],(j==i-1)?'\n':' ');
// printf("D: ");for(int j=0;j<i;j++) printf("%d%c",D[j],(j==i-1)?'\n':' ');
NTT(C,i<<1,1);NTT(D,i<<1,1);
for(int j=0;j<(i<<1);j++) E[j]=1ll*C[j]*D[j]%MOD*D[j]%MOD;
NTT(E,i<<1,-1);
// printf("E: ");for(int j=0;j<(i<<1);j++) printf("%d%c",E[j],(j==(i<<1)-1)?'\n':' ');
for(int j=0;j<i;j++) b[j]=(2*b[j]%MOD-E[j]+MOD)%MOD;
}
// for(int i=0;i<len;i++) printf("%d%c",b[i],(i==len-1)?'\n':' ');
}
int main(){
scanf("%d",&n);ipr=qpow(pr,MOD-2);
for(int i=0;i<n;i++) scanf("%d",&f[i]);
while(LEN<=n) LEN<<=1,LOG++;
for(int i=1;i<=(LEN<<1);i++) inv[i]=qpow(i,MOD-2);
for(int i=1;i<=(LEN<<1);i<<=1){
prs[i][0]=qpow(pr,(MOD-1)/i);
prs[i][1]=qpow(ipr,(MOD-1)/i);
}
diff(f,A,LEN);getinv(f,B,LEN);
// for(int i=0;i<LEN;i++) printf("%d%c",A[i],(i==LEN-1)?'\n':' ');
// for(int i=0;i<LEN;i++) printf("%d%c",B[i],(i==LEN-1)?'\n':' ');
NTT(A,LEN<<1,1);NTT(B,LEN<<1,1);
for(int i=0;i<LEN<<1;i++) g[i]=1ll*A[i]*B[i]%MOD;
NTT(g,LEN<<1,-1);integrate(g,h,LEN);
for(int i=0;i<n;i++) printf("%d%c",h[i],(i==n-1)?'\n':' ');
return 0;
}
/*
5
1 6 3 4 9
*/
多项式除法
23. P4512 【模板】多项式除法
感觉是个挺神仙的玩意儿,虽然不常考,但还是看看吧。
对于一个 \(n\) 次多项式 \(F(x)\),我们考虑下式的含义:
我们发现,\(F(x)\) 里面每一项 \(f_ix^i\),到 \(F^R(x)\) 里都会变成 \(f_ix^{n-i}\),也就是说我们对整个多项式进行了一遍系数的转置。
那么这个转置有什么意义吗?考虑多项式除法中,我们要找到两个多项式 \(Q(x),R(x)\) 满足 \(A(x)=B(x)Q(x)+R(x)\)。
两边同时将 \(x\) 替换为 \(\dfrac{1}{x}\),再同乘 \(x^n\) 即有:
我们发现,后面的 \(R^R(x)\) 的非零最低位就已经达到了 \(x^{n-m+1}\),而 \(Q(x)\) 的最高位才 \(x^{n-m}\)。故此时我们就消除了 \(R(x)\) 产生的影响。此时我们只需对 \(B^R(x)\) 求一遍模 \(x^{n-m}\) 的逆元就可以算得 \(Q(x)\)。再代回原式就能求出 \(R(x)\) 了。
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int pr=3;
const int MAXP=1<<18;
const int MOD=998244353;
int qpow(int x,int e){int ret=1;for(;e;e>>=1,x=1ll*x*x%MOD) if(e&1) ret=1ll*ret*x%MOD;return ret;}
int n,m,a[MAXP+5],b[MAXP+5],c[MAXP+5];
int A[MAXP+5],B[MAXP+5],C[MAXP+5],D[MAXP+5];
int LEN=1,LOG=0,inv[MAXP+5],rev[MAXP+5],prs[MAXP+5][2],ipr;
void NTT(int *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
int W=prs[i][type<0];
for(int j=0;j<len;j+=i){
int w=1;
for(int k=0;k<(i>>1);k++,w=1ll*w*W%MOD){
int X=a[j+k],Y=1ll*w*a[(i>>1)+j+k]%MOD;
a[j+k]=(X+Y)%MOD;a[(i>>1)+j+k]=(X-Y+MOD)%MOD;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i]=1ll*a[i]*inv[len]%MOD;
}
void polymul(int *a,int *b,int *c,int len){
for(int i=0;i<len;i++) A[i]=B[i]=0;
for(int i=0;i<len;i++) A[i]=a[i],B[i]=b[i];
NTT(A,len,1);NTT(B,len,1);
for(int i=0;i<len;i++) c[i]=1ll*A[i]*B[i]%MOD;
NTT(c,len,-1);
}
void getinv(int *a,int *b,int len){
for(int i=0;i<len;i++) b[i]=0;
b[0]=qpow(a[0],MOD-2);
for(int i=2;i<=len;i<<=1){
for(int j=0;j<(i<<1);j++) C[j]=D[j]=0;
for(int j=0;j<i;j++) C[j]=a[j];
for(int j=0;j<(i>>1);j++) D[j]=b[j];
polymul(D,D,D,i);polymul(C,D,C,i<<1);
for(int j=0;j<i;j++) b[j]=(2*b[j]%MOD-C[j]+MOD)%MOD;
}
}
int main(){
scanf("%d%d",&n,&m);ipr=qpow(pr,MOD-2);
for(int i=0;i<=n;i++) scanf("%d",&a[i]);
for(int i=0;i<=m;i++) scanf("%d",&b[i]);
reverse(a,a+n+1);reverse(b,b+m+1);
while(LEN<=n) LEN<<=1,LOG++;
for(int i=1;i<=(LEN<<1);i<<=1){
inv[i]=qpow(i,MOD-2);
prs[i][0]=qpow(pr,(MOD-1)/i);
prs[i][1]=qpow(ipr,(MOD-1)/i);
}
getinv(b,c,LEN);polymul(a,c,c,LEN<<1);
reverse(c,c+n-m+1);for(int i=n-m+1;i<(LEN<<1);i++) c[i]=0;
for(int i=0;i<=n-m;i++) printf("%d%c",c[i],(i==n-m)?'\n':' ');
reverse(b,b+m+1);reverse(a,a+n+1);polymul(b,c,c,LEN<<1);
for(int i=0;i<m;i++) printf("%d%c",(a[i]-c[i]+MOD)%MOD,(i==m-1)?'\n':' ');
return 0;
}
好了,下面真正神仙的东西就要来了→
多项式 exp
在学这个之前,我们先聊点儿别的。
泰勒展开
可以看看这里第一个回答,非常通俗易懂。这里介绍我对其的理解。
假设我们现在有个函数 \(F(x)\),它不是形式幂级数的形式,譬如上面例子中的 \(\cos(x)\),我们想把它表示为形式幂级数,即 \(G(x)=\sum\limits_ia_ix^i\),的形式。
我们先随便选定一个点,就以 \(0\) 为例,我们希望 \(G(x)\) 与 \(F(x)\) 尽可能重合,所以我们令 \(G(0)=F(0)\)。
但显然仅仅满足 \(G(0)=F(0)\) 的形式幂级数有无数多个,有的甚至与 \(F(x)\) 相去甚远。那么有什么解决办法吗?难道再代一个特殊值吗?一氧化氮。
注意到如果 \(F\) 与 \(G\) 重合,那么它们在 \(0\) 处的导数应当相同。故我们再令 \(G'(0)=F'(0)\),即 \(F\) 在 \(0\) 处的导数与 \(G\) 在 \(0\) 处的导数相等。但显然即使多了这个条件还有无数个满足条件的 \(G(x)\)。故考虑再令 \(G''(0)=F''(0)\),\(G^{(3)}(0)=F^{(3)}(0)\),以此类推。
那么我们展开来的多项式长啥样呢?显然你求完 \(n\) 阶导,再代入 \(0\) 后就只剩下常数项了。而求完 \(n\) 阶导后的常数项实际上是 \(n!a_n\),故我们有 \(a_n=\dfrac{F^{(n)}(0)}{n!}\)。于是 \(G(x)=F(0)+\dfrac{F^{(1)}{(0)}}{1!}x+\dfrac{F^{(2)}{(0)}}{2!}x^2+\dfrac{F^{(3)}{(0)}}{3!}x^3+\dots+\dfrac{F^{(r)}(0)}{r!}x^r+\dots\)
在上述例子中我们是以 \(0\) 为关键点的,如果我们将这里的 \(0\) 换为 \(x_0\),重复上面的步骤也可得出类似的表达式:
当然有时候我们不可能无止尽地递归下去,譬如我们只觉得只求 \(n\) 阶导就足够了。于是我们又有了如下的结论:
其中 \(R_n(x)\) 被称为泰勒公式的拉格朗日余项。
当 \(x_0=0\) 的时候,上述式子又被称为 \(F(x)\) 的麦克劳林展开式。
给出几个常见的函数的麦克劳林展开式吧:
\(e^x=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\dfrac{x^4}{4!}+\dots\)
\(\cos(x)=1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\dfrac{x^6}{6!}+\dfrac{x^8}{8!}\dots\)
\(\sin(x)=x-\dfrac{x^3}{3!}+\dfrac{x^5}{5!}-\dfrac{x^7}{7!}+\dfrac{x^9}{9!}\dots\)
\(\ln(1+x)=x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\dfrac{x^4}{4}+\dfrac{x^5}{5}\dots\)
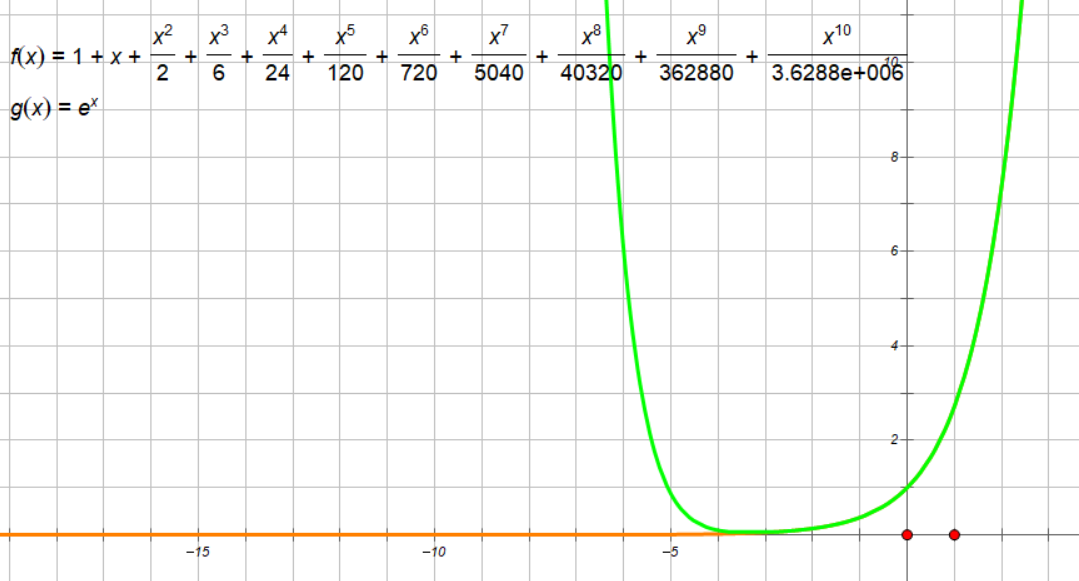
最后,附上一张图,其中绿色函数为 \(y=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\dots+\dfrac{x^{10}}{10!}\),橙色函数为 \(y=e^x\),你可以清楚地发现,橙色函数图像与绿色函数图像后半部分几乎是重合的:
牛顿迭代
你可能会问:泰勒展开在多项式中有什么实际应用吗?
答曰:牛顿迭代。
牛顿迭代可以用来解决类似于求 \(G(F(x))\equiv 0\pmod{x^n}\) 的 \(F(x)\) 的问题。其中 \(G(x)\) 一般只涉及比较基础的运算,如平方,取 \(\ln\) 等等。
考虑倍增。假设我们已经求得 \(G(F_0(x))\equiv 0\pmod{x^{n/2}}\)。
将 \(G(F(x))\) 在 \(F_0(x)\) 处泰勒展开可以得到 \(G(F(x))\equiv G(F_0(x))+G'(F_0(x))(F(x)-F_0(x))+\dfrac{G''(F_0(x))}{2!}(F(x)-F_0(x))^2\dots\pmod{x^n}\)
不难发现,由于 \(F_0(x)\equiv F(x)\pmod{x^{n/2}}\),\((F_0(x)-F(x))^2\) 的系数非零的最低项至少为 \(x^n\),故从第三项开始,每项都是 \(x^n\) 的倍数,故我们只保留前两项。
\(G(F(x))\equiv G(F_0(x))+G'(F_0(x))(F(x)-F_0(x))\pmod{x^n}\)
由于 \(G(F(x))\equiv 0\pmod{x^n}\),我们有
\(G'(F_0(x))F(x)\equiv G'(F_0(x))F_0(x)-G(F_0(x))\pmod{x^n}\)
\(F(x)\equiv F_0(x)-\dfrac{G(F_0(x))}{G'(F_0(x))}\pmod{x^n}\)
以上就是牛顿迭代的全部内容。
好了终于可以进入正题了
24. P4726 【模板】多项式指数函数(多项式 exp)
我们要求满足 \(F(x)\equiv e^{A(x)}\pmod{x^n}\) 的 \(F(x)\)
两边同时取 \(\ln\) 可以得到 \(\ln F(x)\equiv A(x)\pmod{x^n}\)
设 \(G(F(x))=\ln F(x)-A(x)\),我们的目标是求满足 \(G(F(x))\equiv 0\pmod{x^n}\) 的 \(F(x)\)
假设我们已经求得 \(G(F_0(x))\equiv 0\pmod{x^{n/2}}\)
对上面这坨东西进行牛顿迭代可得 \(F(x)\equiv F_0(x)-\dfrac{G(F_0(x))}{G'(F_0(x))}\)
即 \(F(x)\equiv F_0(x)-\dfrac{\ln F_0(x)-A(x)}{\dfrac{1}{F_0(x)}}\pmod{x^n}\)
\(F(x)\equiv F_0(x)(1-\ln F_0(x)+A(x))\pmod{x^n}\)
分治的过程中求一遍卷积,一遍多项式 \(\ln\) 即可。
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int pr=3;
const int MAXP=1<<18;
const int MOD=998244353;
int qpow(int x,int e){int ret=1;for(;e;e>>=1,x=1ll*x*x%MOD) if(e&1) ret=1ll*ret*x%MOD;return ret;}
int n,a[MAXP+5],b[MAXP+5];
int LEN=1,LOG=0,rev[MAXP+5],prs[MAXP+5][2],inv[MAXP+5],ipr;
int A[MAXP+5],B[MAXP+5],C[MAXP+5],D[MAXP+5],E[MAXP+5],F[MAXP+5],G[MAXP+5],H[MAXP+5],I[MAXP+5];
void NTT(int *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
int W=prs[i][type<0];
for(int j=0;j<len;j+=i){
int w=1;
for(int k=0;k<(i>>1);k++,w=1ll*w*W%MOD){
int X=a[j+k],Y=1ll*a[(i>>1)+j+k]*w%MOD;
a[j+k]=(X+Y)%MOD;a[(i>>1)+j+k]=(X-Y+MOD)%MOD;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i]=1ll*a[i]*inv[len]%MOD;
}
void polymul(int *a,int *b,int *c,int len){
for(int i=0;i<len;i++) A[i]=B[i]=0;
for(int i=0;i<len;i++) A[i]=a[i],B[i]=b[i];
NTT(A,len,1);NTT(B,len,1);
for(int i=0;i<len;i++) c[i]=1ll*A[i]*B[i]%MOD;
NTT(c,len,-1);
}
void getinv(int *a,int *b,int len){
for(int i=0;i<len;i++) b[i]=0;
b[0]=qpow(a[0],MOD-2);
for(int i=2;i<=len;i<<=1){
for(int j=0;j<(i<<1);j++) C[j]=D[j]=0;
for(int j=0;j<i;j++) C[j]=a[j];
for(int j=0;j<(i>>1);j++) D[j]=b[j];
polymul(D,D,D,i);polymul(C,D,C,i<<1);
for(int j=0;j<i;j++) b[j]=(2*b[j]%MOD-C[j]+MOD)%MOD;
}
}
void direv(int *a,int *b,int len){
for(int i=1;i<len;i++) b[i-1]=1ll*a[i]*i%MOD;b[len-1]=0;
}
void inter(int *a,int *b,int len){
for(int i=1;i<len;i++) b[i]=1ll*a[i-1]*inv[i]%MOD;b[0]=0;
}
void getln(int *a,int *b,int len){
for(int i=0;i<(len<<1);i++) E[i]=F[i]=G[i]=0;
direv(a,E,len);getinv(a,F,len);
polymul(E,F,E,len<<1);
for(int i=0;i<len;i++) G[i]=E[i];
inter(G,b,len);
}
void getexp(int *a,int *b,int len){
for(int i=0;i<len;i++) b[i]=H[i]=I[i]=0;
b[0]=1;
for(int i=2;i<=len;i<<=1){
for(int j=0;j<(i<<1);j++) H[j]=I[j]=0;
// printf("H: ");for(int j=0;j<i;j++) printf("%d%c",b[j],(j==i-1)?'\n':' ');
getln(b,H,i);
// printf("ln H: ");for(int j=0;j<i;j++) printf("%d%c",H[j],(j==i-1)?'\n':' ');
for(int j=0;j<i;j++) H[j]=(-H[j]+a[j]+MOD)%MOD;
(H[0]+=1)%=MOD;
for(int j=0;j<(i>>1);j++) I[j]=b[j];
polymul(H,I,H,(i<<1));
for(int j=0;j<i;j++) b[j]=H[j];
}
}
int main(){
scanf("%d",&n);ipr=qpow(pr,MOD-2);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
while(LEN<=n) LEN<<=1,LOG++;
for(int i=1;i<=(LEN<<1);i++) inv[i]=qpow(i,MOD-2);
for(int i=1;i<=(LEN<<1);i<<=1){
prs[i][0]=qpow(pr,(MOD-1)/i);
prs[i][1]=qpow(ipr,(MOD-1)/i);
} getexp(a,b,LEN);
for(int i=0;i<n;i++) printf("%d%c",b[i],(i==n-1)?'\n':' ');
return 0;
}
多项式快速幂
25. P5245 【模板】多项式快速幂
根据对数的性质,显然有 \(F^k(x)=e^{k\ln F(x)}\)
求出 \(\ln F(x)\),乘个 \(k\),再求遍多项式 exp 即可。
但是这里的 \(k\) 很大,需要对其取模。
令我很自闭的是这题调了整整 1.5h,只因为再求 \(\ln\) 的时候数组只清到了 \(n\),而求 \(\ln\) 的时候我们要对两个长度为 \(n\) 的多项式求卷积,故应当清到 \(2n\)。
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int pr=3;
const int MAXP=1<<18;
const int MOD=998244353;
int n,m,a[MAXP+5],b[MAXP+5],c[MAXP+5];char buf[MAXP+5];
int qpow(int x,int e){
int ret=1;
for(;e;e>>=1,x=1ll*x*x%MOD) if(e&1) ret=1ll*ret*x%MOD;
return ret;
}
int LEN=1,LOG=0,inv[MAXP+5],rev[MAXP+5],prs[MAXP+5][2],ipr;
int A[MAXP+5],B[MAXP+5],C[MAXP+5],D[MAXP+5],E[MAXP+5];
int F[MAXP+5],G[MAXP+5],H[MAXP+5],I[MAXP+5],J[MAXP+5];
void NTT(int *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
int W=prs[i][type<0];
for(int j=0;j<len;j+=i){
int w=1;
for(int k=0;k<(i>>1);k++,w=1ll*w*W%MOD){
int X=a[j+k],Y=1ll*a[(i>>1)+j+k]*w%MOD;
a[j+k]=(X+Y)%MOD;a[(i>>1)+j+k]=(X-Y+MOD)%MOD;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i]=1ll*a[i]*inv[len]%MOD;
}
void polymul(int *a,int *b,int *c,int len){
for(int i=0;i<len;i++) A[i]=B[i]=0;
for(int i=0;i<len;i++) A[i]=a[i],B[i]=b[i];
NTT(A,len,1);NTT(B,len,1);
for(int i=0;i<len;i++) c[i]=1ll*A[i]*B[i]%MOD;
NTT(c,len,-1);
}
void getinv(int *a,int *b,int len){
for(int i=0;i<len;i++) b[i]=0;
b[0]=qpow(a[0],MOD-2);
for(int i=2;i<=len;i<<=1){
for(int j=0;j<(i<<1);j++) C[j]=D[j]=0;
for(int j=0;j<i;j++) C[j]=a[j];
for(int j=0;j<(i>>1);j++) D[j]=b[j];
polymul(D,D,D,i);polymul(C,D,C,i<<1);
for(int j=0;j<i;j++) b[j]=(2*b[j]%MOD-C[j]+MOD)%MOD;
}
}
void direv(int *a,int *b,int len){
for(int i=1;i<len;i++) b[i-1]=1ll*a[i]*i%MOD;b[len-1]=0;
}
void inter(int *a,int *b,int len){
for(int i=1;i<len;i++) b[i]=1ll*a[i-1]*inv[i]%MOD;b[0]=0;
}
void getln(int *a,int *b,int len){
for(int i=0;i<(len<<1);i++) E[i]=F[i]=G[i]=0;
direv(a,E,len);getinv(a,F,len);
polymul(E,F,E,len<<1);
for(int i=0;i<len;i++) G[i]=E[i];
inter(G,b,len);
}
void getexp(int *a,int *b,int len){
for(int i=0;i<len;i++) b[i]=0;
b[0]=1;
for(int i=2;i<=len;i<<=1){
for(int j=0;j<(i<<1);j++) H[j]=I[j]=0;
// printf("H: ");for(int j=0;j<i;j++) printf("%d%c",b[j],(j==i-1)?'\n':' ');
getln(b,H,i);
// printf("ln H: ");for(int j=0;j<i;j++) printf("%d%c",H[j],(j==i-1)?'\n':' ');
for(int j=0;j<i;j++) H[j]=(-H[j]+a[j]+MOD)%MOD;
(H[0]+=1)%=MOD;
for(int j=0;j<(i>>1);j++) I[j]=b[j];
polymul(H,I,H,(i<<1));
for(int j=0;j<i;j++) b[j]=H[j];
}
}
void getksm(int *a,int *b,int k,int len){
getln(a,J,len);
// for(int i=0;i<len;i++) printf("%d%c",J[i],(i==len-1)?'\n':' ');
for(int i=0;i<len;i++) J[i]=1ll*J[i]*k%MOD;
getexp(J,b,len);
}
int main(){
scanf("%d%s",&n,buf+1);int len=strlen(buf+1);
for(int i=0;i<n;i++) scanf("%d",&a[i]);ipr=qpow(pr,MOD-2);
for(int i=1;i<=len;i++) m=(10ll*m+(buf[i]^48))%MOD;
while(LEN<=n) LEN<<=1,LOG++;
for(int i=1;i<=(LEN<<2);i++) inv[i]=qpow(i,MOD-2);
for(int i=1;i<=(LEN<<2);i<<=1){
prs[i][0]=qpow(pr,(MOD-1)/i);
prs[i][1]=qpow(ipr,(MOD-1)/i);
} getksm(a,b,m,LEN);
for(int i=0;i<n;i++) printf("%d%c",b[i],(i==n-1)?'\n':' ');
return 0;
}
好的这里就是多项式全家桶的全部内容了。
什么?你说还有三角函数、复合逆什么的?包括还有多项式开根、多项式快速幂的加强版。那玩意大概用不到吧……等到被卡毒瘤题的时候再学罢。。。
下转多项式 Ⅱ


