Codeforces 506E - Mr. Kitayuta's Gift(神仙矩阵乘法)
神仙题 %%%%%%%%%%%%%
u1s1 感觉这道题风格很省选(
下记 \(m=|s|\),首先探讨 \(n+m\) 为偶数的情形。
首先考虑一个暴力的 DP,我们设 \(dp_{i,l,r}\) 表示当前考虑了回文串的前 \(i\) 个字符和后 \(i\) 个字符,前 \(i\) 个字符恰好匹配了 \(s\) 的 \([1,l-1]\) 区间中的字符,后 \(i\) 个字符恰好匹配了 \(s\) 的 \([r+1,m]\) 区间中的字符的方案数,再记 \(g_i\) 为当前考虑了回文串的前 \(i\) 个字符和后 \(i\) 个字符。
考虑转移,分四种情况:
- \(r-l\le 1\) 且 \(s_l=s_r\),那么如果我们在 \(i+1\) 位置填上 \(s_l\) 那么就匹配结束了,即 \(g_{i+1}\leftarrow dp_{i,l,r}\),否则还是只能完全匹配 \([1,l-1]\) 和 \([r+1,n]\) 中的字符,即 \(dp_{i+1,l,r}\leftarrow 25·dp_{i,l,r}\)。
- \(r-l\ge 2\) 且 \(s_l=s_r\),那么如果我们在从左往右数和从右往左数第 \(i+1\) 的位置填上 \(s_l\) 就可以匹配到 \([1,l]\) 和 \([r,m]\),即 \(dp_{i+1,l+1,r-1}\leftarrow dp_{i,l,r}\),否则还是有 \(dp_{i+1,l,r}\leftarrow 25·dp_{i,l,r}\)
- \(s_l\ne s_r\),那么如果我们在从左往右数和从右往左数第 \(i+1\) 的位置填 \(s_l\),左端点就可以多匹配一位,即 \(dp_{i+1,l+1,r}\leftarrow dp_{i,l,r}\),同理如果我们填 \(s_r\),右端点就可以多匹配一位,即 \(dp_{i+1,l,r-1}\leftarrow dp_{i,l,r}\),否则还是只能完全匹配 \([1,l-1]\) 和 \([r+1,n]\) 中的字符,即 \(dp_{i+1,l,r}\leftarrow 24·dp_{i,l,r}\)。
- \(g\) 的转移:显然由于我们已经匹配结束了,剩下的位置填什么都行,即 \(g_{i+1}\leftarrow 26·g_i\)。
最终答案即为 \(g_{(n+m)/2}\)
这样暴力是 \(nm^2\) 的,如果强行把 \((l,r)\) 看作一个二元组套矩乘,那可以实现 \(m^6\log n\) 的优秀复杂度,一脸过不去。
我们考虑优化,敏感一些的同学应该可以注意到这个 DP 转移方程有点像 DAG 上的 DP,事实上,如果我们把所有二元组 \((l,r)\) 以及 \(g_i\)(下记为目标点)分别看作一个点,对于形如 \(dp_{i+1,x}\leftarrow z·dp_{i,y}\) 的状态转移方程式,我们就从 \(y\) 到 \(x\) 连 \(z\) 条边,那么答案就是 \((1,m)\) 表示的点到目标点的经过 \(\dfrac{n+m}{2}\) 条边的路径条数。
我们考虑探究一下这张图长啥样,比方说 \(s=\text{abaac}\),那么建出图来就长这样(这里借用了 xht37 大佬题解里的图):
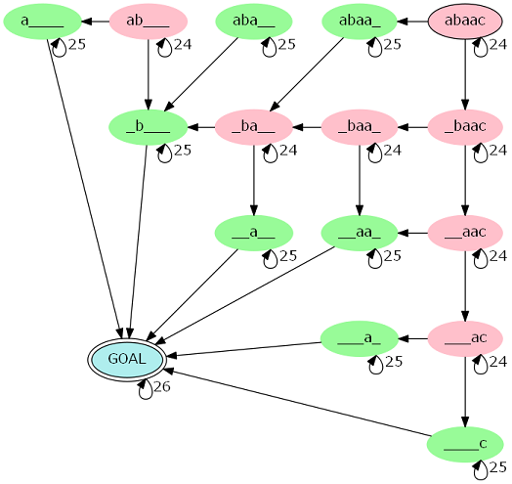
不难发现,该图是由若干个自环即若干条有向边组成了,对于每个状态 \((l,r)\) 都有一个自环连向自己,如果去掉这些自环,那形成的图显然是一个 DAG(\((l,r)\) 能到达 \((l',r')\) 当且仅当 \([l',r']\subseteq[l,r]\),这显然构成了一个偏序关系),也就是说从源点 \((1,m)\) 到目标点,经过的非自环边的个数最多只有 \(m\)(每次经过一条边,区间长度缩小 \(1\) 或 \(2\),因此至少缩小 \(m\) 次就能到达目标点)
并且还可以发现除了目标点上有个 \(26\) 的自环之外,自环的类型只有 \(2\) 种,那就是权值为 \(25\) 的环和权值为 \(24\) 的环,我们不妨称存在权值为 \(25\) 的自环连向自己的点为“\(25\) 点”,其余的点称为“\(24\) 点”。考虑观察这个路径个数有什么性质,我们不妨称去掉自环边后路径相同的路径为等价类,考虑对每个等价类计算一遍方案数,容易发现等价类具体先经过权值为多少的自环,后经过权值为多少的自环并不重要,我们只关心它经过了多少权值为 \(24,25,26\) 的自环,即两个等价类的路径的个数相同当且仅当这两个等价类的路径上 \(24,25,26\) 的自环的个数相同。
显然权值为 \(26\) 的自环就是废话,因为从起始点到目标点总共只会经过一个 \(26\) 的自环。而经过的 \(25\) 的自环和 \(24\) 的自环个数有一个性质,那就是如果我们记经过的 \(25\) 的自环个数为 \(c_{25}\),经过的 \(24\) 的自环个数为 \(c_{24}\),则 \(c_{25}=\lceil\dfrac{s-c_{24}}{2}\rceil\),道理很简单,对于一个 \(25\) 点 \([l,r]\),每当我们从该点走向一个别的点时,区间长度会缩短 \(2\)(当然 \(l=r\) 时只会缩短 \(1\)),而对于一个 \(24\) 点 \([l,r]\) 则会缩短 \(1\),因此 \(c_{25}=\lceil\dfrac{s-c_{24}}{2}\rceil\),故我们只需对于每个 \(i\) 求出经过 \(i\) 个 \(24\) 点的等价类个数,然后对每个 \(i\) 跑一遍矩阵快速幂即可。
这个东西怎么求呢?考虑记忆化搜索,记 \(f_{x,l,r}\) 为以状态 \([l,r]\) 为结尾的经过 \(x+[(l,r)\text{是否为}24\text{点}]\) 个 \(24\) 点的路径个数,转移很容易,如果 \(s_{l-1}\ne s_r\) 那 \((l-1,r)\) 为 \(24\) 点并且存在 \((l-1,r)\to (l,r)\) 的边,\(f_{x,l,r}\leftarrow f_{x,l,r}\),\((l,r+1)\) 也同理,如果 \(s_{l-1}=s_{r+1}\),那 \((l-1,r+1)\) 为 \(25\) 点并且存在 \((l-1,r+1)\to(l+r)\) 的边,\(f_{x,l,r}\leftarrow f_{x,l-1,r+1}\),记忆化搜索即可,边界条件 \(f_{0,1,m}=1\)。
这样复杂度是 \(m^4\log n\) 的,还是无法通过,继续优化。
这题复杂度瓶颈在于对于每个 \(x\) 都跑一遍矩阵优化,考虑对状态进行压缩,我们在上面建一排 \(m\) 个 \(24\) 点,在下面建一排 \(\lceil\dfrac{m}{2}\rceil\) 个 \(25\) 点,对于上面一排的第 \(i\) 个点,连一条指向第二排第 \(\lceil\dfrac{m}{2}\rceil-\lceil\dfrac{m-i}{2}\rceil\) 个节点,权值为经过 \(i\) 个路径的等价类个数,然后在相邻的 \(24\) 点之间连权值为 \(1\) 的边,在相邻的 \(25\) 点之间连权值为 \(1\) 的边,然后每个 \(24\) 点上都套个权值为 \(24\) 的自环,每个 \(25\) 点上套个权值为 \(25\) 的自环,最后连一条从最右边的 \(25\) 点向目标点,权值为 \(1\) 的边,再在目标点上套个 \(26\) 的自环即可。这里还是借一张 xht37 神仙题解里的图:
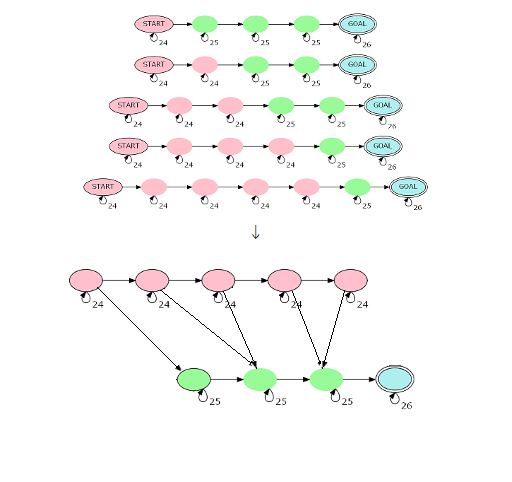
这样状态数降低到了 \(\mathcal O(m)\),跑一遍矩乘即可,复杂度 \(m^3\log n\)。
这仅仅只是 \(n+m\) 为偶数的情况,最后考虑 \(n+m\) 为奇数的情况有什么不同。记 \(p=\dfrac{n+m-1}{2}\),唯一的不同就是最后一步,\(dp_{p,i,i+1}\)(\(s_i=s_{i+1}\)),无法转移到 \(g_{p+1}\)。正难则反,我们考虑拿总方案数减去这部分方案数,我们只需保留最后一步从 \((i,i+1)\) 转移的链,并去掉目标点上 \(26\) 的自环即可。
最后,此题还存在卡常数的问题。这里有一个小技巧,那就是由于我们只在 \((i,j)(i<j)\) 的状态之间连边,得到的矩阵是一个下三角矩阵(我代码里使用的是先矩阵、后向量的乘法,因此对于存在边的 \((i,j)\) 我是令 \(j\) 为行号 \(i\) 为列号,因此得到的是上三角矩阵,不过差不多辣),因此我们在矩阵乘法时候只需枚举 \(1\le i\le k\le j\) 的 \((i,j,k)\),这样常数可以减小到原来的 \(\dfrac{1}{6}\)
u1s1 这题题解码死我了
话说这场的 D1C D E 我是不是都做过了啊,u1s1 这场的 C 我都不会。
const int MAXN=200;
const int MAXM=300;
const int MOD=1e4+7;
int n,m,k;char s[MAXN+5];
struct mat{
ll a[MAXM+5][MAXM+5];
mat(){memset(a,0,sizeof(a));}
mat operator *(const mat &rhs){
mat res;
for(int i=1;i<=k;i++) for(int l=1;l<=i;l++) for(int j=1;j<=l;j++)
res.a[i][j]+=a[i][l]*rhs.a[l][j];
for(int i=1;i<=k;i++) for(int j=1;j<=k;j++) res.a[i][j]%=MOD;
return res;
}
};
int dp[MAXN+5][MAXN+5][MAXN+5];
int dfs(int x,int l,int r){
if(x<0) return 0;
if(~dp[x][l][r]) return dp[x][l][r];
if(l==1&&r==m) return dp[x][l][r]=(!x);
dp[x][l][r]=0;
if(l!=1&&s[l-1]!=s[r]) dp[x][l][r]=(dp[x][l][r]+dfs(x-1,l-1,r))%MOD;
if(r!=m&&s[l]!=s[r+1]) dp[x][l][r]=(dp[x][l][r]+dfs(x-1,l,r+1))%MOD;
if(l!=1&&r!=m&&s[l-1]==s[r+1]) dp[x][l][r]=(dp[x][l][r]+dfs(x,l-1,r+1))%MOD;
return dp[x][l][r];
}
int main(){
scanf("%s%d",s+1,&n);m=strlen(s+1);k=m+((m+1)>>1);
memset(dp,-1,sizeof(dp));mat st,trs,res;
for(int i=0;i<m;i++){
int cnt=0;
for(int j=1;j<=m;j++){
cnt=(cnt+dfs(i,j,j))%MOD;
if((j^m)&&!(s[j]^s[j+1])) cnt=(cnt+dfs(i,j,j+1))%MOD;
}
// printf("%d %d\n",i,cnt);
if(i) trs.a[k-((m-i+1)>>1)][i]=cnt;
else st.a[m][1]=cnt;
}
for(int i=2;i<m;i++) trs.a[i][i-1]=1;
if(m>1) st.a[1][1]=1;
for(int i=m;i<k;i++) trs.a[i+1][i]=1;
for(int i=1;i<m;i++) trs.a[i][i]=24;
for(int i=m;i<k;i++) trs.a[i][i]=25;
trs.a[k][k]=26;
for(int i=1;i<=k;i++) res.a[i][i]=1;
// for(int i=1;i<=k;i++) for(int j=1;j<=k;j++) printf("%d%c",trs.a[i][j],(j==k)?'\n':' ');
int stp=(n+m+1)>>1;
for(;stp;stp>>=1,trs=trs*trs) if(stp&1) res=res*trs;
// for(int i=1;i<=k;i++) for(int j=1;j<=k;j++) printf("%d%c",res.a[i][j],(j==k)?'\n':' ');
int sum=0;for(int i=1;i<=k;i++) sum=(sum+st.a[i][1]*res.a[k][i])%MOD;
if(!((n+m)&1)) return printf("%d\n",sum),0;
int ans=sum;
memset(res.a,0,sizeof(res.a));memset(trs.a,0,sizeof(trs.a));
memset(st.a,0,sizeof(st.a));
for(int i=0;i<m;i++){
int cnt=0;
for(int j=1;j<=m;j++){
if((j^m)&&!(s[j]^s[j+1])) cnt=(cnt+dfs(i,j,j+1))%MOD;
}
if(i) trs.a[k-((m-i+1)>>1)][i]=cnt;
else st.a[m][1]=cnt;
}
for(int i=2;i<m;i++) trs.a[i][i-1]=1;
if(m>1) st.a[1][1]=1;
for(int i=m;i<k;i++) trs.a[i+1][i]=1;
for(int i=1;i<m;i++) trs.a[i][i]=24;
for(int i=m;i<k;i++) trs.a[i][i]=25;
for(int i=1;i<=k;i++) res.a[i][i]=1;
stp=(n+m+1)>>1;
for(;stp;stp>>=1,trs=trs*trs) if(stp&1) res=res*trs;
sum=0;for(int i=1;i<=k;i++) sum=(sum+st.a[i][1]*res.a[k][i])%MOD;
printf("%d\n",(ans-sum+MOD)%MOD);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号