AC 自动机学习笔记
虽然 NOIp 原地爆炸了,目前进入 AFO 状态,但感觉省选还是要冲一把,所以现在又来开始颓字符串辣
首先先复习一个很早很早就学过但忘记的算法——自动 AC AC自动机。
AC 自动机能够在 \(\mathcal O(\sum|s|)\) 的时间内解决多模式串的问题,你可以理解为它把 KMP 放在了 trie 树上。
举个例子,\(S=\{"abc","bcd","cd"\},T="abcdbc"\)。
首先建出 trie 树:
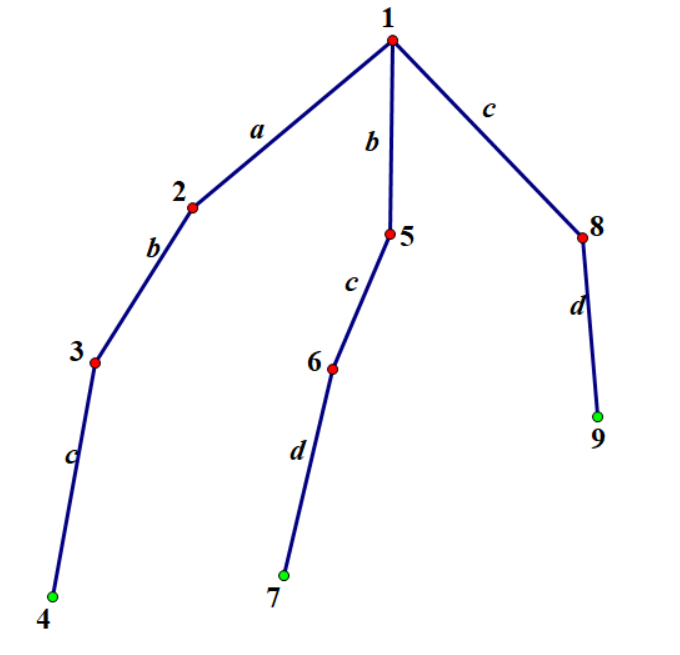
我们沿着 trie 树的边走,\(1\to 2\to 3\to 4\),发现成功匹配了字符串 \("abc"\)。
现在问题来了,\(T\) 的下一位是 \(d\),而我们当前在 \(4\) 号节点已经无路可走了,怎么办呢?
如果我们现在重新回到根节点,那么运行效率就会变得非常低下。
此时我们可以借鉴 KMP 的思想。由于我们已经知道当前字符串的前三位是 \("abc"\) 了,而 \(6\) 号节点对应的节点表示的字符串 \("bc"\) 刚好是 \("abc"\) 的后缀,并且 \(6\) 号节点刚好有个 "\(d\) 儿子" \(7\)。此时我们就可以将指针移到 \(7\) 号节点,并继续往下匹配。
回忆起在学习 KMP 的时候定义了一个 \(fail\) 数组表示最长公共前后缀的长度,类似地,在 AC 自动机中我们也可以定义一个 \(fail_i\) 表示在节点 \(i\) 失配了应当跳到哪个节点的位置。
具体地来说 \(fail_i=j\) 表示:
- \(j\) 到根节点的路径组成的字符串是 \(i\) 到根节点的路径组成的字符串的后缀且 \(j\neq i\)
- \(j\) 是这样的节点中深度最大的。
怎样求 \(fail_i\) 呢?
记 \(s(u)\) 为根节点到 \(u\) 的路径上的字符串,\(fa_i\) 为 \(i\) 的父亲节点。
根据 \(fail\) 的定义,\(s(fail_i)\) 是 \(s(i)\) 的后缀。
如果 \(fail_i\) 不是根节点,那么 \(s(fail_i)\) 去掉最后一位得到的字符串后肯定也是 \(s(i)\) 去掉最后一位后得到的字符串的后缀。
而 \(s(i)\) 去掉最后一位后得到的字符串就是 \(s(fa_i)\),\(s(fail_i)\) 去掉最后一位后得到的字符串为 \(s(fa[fail[i]])\)。
在学 KMP 的时候我们学到过一个推论,对于字符串 \(s\) 的某个前缀 \(i\),\(fail[i],fail[fail[i]],fail[fail[fail[i]]]\dots\) 都是该前缀的公共前后缀,并且该前缀的每个公共前后缀都可以表示为 \(fail[fail[fail[\dots]]]\) 的形式。
类似地,如果 \(s(j)\) 是 \(s(i)\) 的后缀,那么 \(j\) 必然可以表示为 \(fail[fail[\dots fail[i]]]\) 的形式 ——【推论】
故 \(fa[fail[i]]]\) 肯定也可以表示为 \(fail[fail[\dots fail[fa[i]]]]\) 的形式。
于是我们可以想到一个做法,\(bfs\),假设当前考虑到节点 \(i\)。
对于节点 \(i\) 的每个 \(c\) 儿子 \(j\):
- 如果 \(fail_i\) 有对应的 \(c\) 儿子,那么 \(fail_j\) 就是 \(fail_i\) 对应的 \(c\) 儿子。
- 否则我们继续查看 \(fail[fail[i]]\) 是否有 \(c\) 儿子,以此类推。
于是我们就可以写出这样的代码:
while(!q.empty()){
int x=q.front();q.pop();
for(int i=0;i<ALPHA;i++) if(ch[x][i]){
int cur=fail[x];while(cur&&!ch[cur][i]) cur=fail[cur];
fail[ch[x][i]]=ch[cur][i];q.push(ch[x][i]);
}
}
然而坏消息是,这样写的复杂度是不对的,因为你每次最坏有可能会跳 \(\mathcal O(n)\) 次。
好消息是,有补救方法:如果 \(i\) 不存在 \(c\) 儿子,就把 \(i\) 的 \(c\) 儿子设为 \(fail_i\) 的 \(c\) 儿子,然后直接引用 \(fail_i\) 的 \(c\) 儿子。稍微感性理解一下就知道这样子是对的并且复杂度也降了下来。
while(!q.empty()){
int x=q.front();q.pop();
for(int i=0;i<ALPHA;i++){
if(ch[x][i]) fail[ch[x][i]]=ch[fail[x]][i],q.push(ch[x][i]);
else ch[x][i]=ch[fail[x]][i];
}
}
这样就可以求出 \(fail\) 数组。
完整代码:
void getfail(){
queue<int> q;
for(int i=0;i<ALPHA;i++) if(ch[0][i]) q.push(ch[0][i]);
while(!q.empty()){
int x=q.front();q.pop();
for(int i=0;i<ALPHA;i++){
if(ch[x][i]) fail[ch[x][i]]=ch[fail[x]][i],q.push(ch[x][i]);
else ch[x][i]=ch[fail[x]][i];
}
}
}
继续回到之前的问题上来,在上一个例子中,我们完整的跳法应该是 \(1 \to 2 \to 3 \to 4 \to 7 \to 5\to 6\),并在 \(4\) 号节点与 \(7\) 号节点处统计了一次答案。
但这样问题就来了,事实上 \(cd\) 也在 \(abcdbc\) 中出现过,而我们并没有在对应节点处(\(8\) 号节点)统计答案。
继续回到 \(abcd\) 的位置,此时此刻我们应当在 \(7\) 号节点,根节点到当前节点的路径为 \(bcd\),而 \(cd\) 为当前字符串的一个后缀。巧的是,\(fail_7\) 就等于 \(8\)。
我们在 \(i\) 节点统计了答案,我们没有计算答案的位置就是那些 \(s(j)\) 是 \(s(i)\) 的后缀,但 \(j\neq i\) 的推论
根据【推论】,如果我们在 \(i\) 处统计了一次答案,那么我们不只在 \(i\) 处的答案 \(+1\),\(fail[i],fail[fail[i]],fail[fail[fail[i]]],\dots\) 的答案也应该 \(+1\)。
这样我们的疑惑就解决了。
下面是例题部分:
洛谷 P3808 【模板】AC自动机(简单版)
模板题,按照上面的方式建 AC 机+暴力跳 \(fail\),只不过加个小小的优化:如果访问过了就设为 \(-1\)。
洛谷 P5357【模板】AC自动机(二次加强版)
这时候暴力跳 \(fail\) 就不太行了。。。
考虑在 \(i\) 与 \(fail_i\) 之间连一条边。
不难发现这样得到的图是一棵有根树。
这样原题变为,有两种操作:
- 将某个点到根节点路径所有点的标记 \(+1\)。
- 求某个点上的标记。
直接离线下来求个前缀和就行了
洛谷 P3121 [USACO15FEB]Censoring G
首先对所有 \(T_i\) 建 AC 自动机。
用栈存储经过的节点的序列。
如果发现到达了某个串的末尾那就弹出栈最后的 \(len\) 个元素,并将它们标记为 \(1\)。
洛谷 P2414 [NOI2011]阿狸的打字机
一道好题,能较好地加深对 AC 自动机的本质的理解。
首先读入的方式比较特别,可以用个栈记录根到当前节点的路径,设第 \(i\) 个串的结束位置为 \(ed_i\)。
老套路,建出 AC 自动机。
根据 AC 自动机的性质,\(x\) 在 \(y\) 出现的次数相当于:在 trie 树上 \(ed_y\) 到根节点的路径上,有多少个节点在 fail 树上在 \(ed_x\) 的子树内。
AC 自动机有个特点,就是不少 AC 自动机的题都能跟树论联系起来,此题至此也转化为一个树论问题。
对 fail 树进行一遍 \(dfs\) ,求出每个点的 \(dfs\) 序。
将每对询问 \((x,y)\) 的信息记录在节点 \(ed_x\) 上。
最后对 trie 树进行一遍 \(dfs\),求出所有询问的答案。访问一个节点的时候将当前节点值 \(+1\),回溯的时候 \(-1\),这样所有 trie 树上在当前节点到根的路径上的节点值都为 \(1\)。
询问的答案就是 \(ed_y\) 的子树内 \(1\) 的个数,可以用树状数组维护。
洛谷 P3966 [TJOI2013]单词
近乎模板的题。
将所有字符串连在一起,不同字符串之间用一个空格隔开,然后跑 P5357 就行了。
洛谷 P5231 [JSOI2012]玄武密码
对所有 \(s\) 建立 AC 自动机并建出 fail 树出来。
用长串 \(t\) 在 AC 自动机上匹配,假设经过的节点为 \(p_1,p_2,\dots,p_{|t|}\)。
显然,这些节点在 fail 树上的祖先所表示的字符串都是在 \(t\) 中出现过的,将它们标记为 \(1\)。
最后对于每个串在树上暴力跳,找出深度最深的被标记为 \(1\) 的点就行了。
洛谷 P5840 [COCI2015]Divljak
又是一道与 AC 自动机与树论结合的题。
我一开始的想法是将 \(s_i\) 和所有新加进来的字符串一起搞出一个 AC 自动机出来,然后发现不太行。
不妨换一个角度,只对 \(s_i\) 建 AC 自动机,并对于每一个新加进来的字符串 \(t\),求出它的贡献。
当我们插入一个 \(t\),就用它在 AC 自动机上匹配,假设匹配经过的节点为 \(p_1,p_2,\dots,p_{|t|}\)。
和上题类似,这些点在 fail 树上的祖先都在 \(t\) 中出现过了,将它们对应的值 \(+1\)。
比较麻烦的一个地方是,本题同一个字符串最多只计算一次贡献,也就是我们要令 \(\cup_{i=1}^{|t|}P(p_i)\) 加 \(1\),其中 \(P(i)\) 为 \(i\) 到根节点路径上节点的集合。
此时就要用到一点树论的技巧了,借鉴 Gym 102082 J Colorful Tree 的技巧,我们将这 \(|t|\) 个节点按 dfs 序排个序,然后在 \(p_i\) 打上标记 \(1\),并在 \(\operatorname{lca}(p_i,p_{i+1})\) 上打上 \(-1\)。
树状数组计算答案,复杂度线性对数。
洛谷 P4052 [JSOI2007]文本生成器
下面开始 AC 自动机与各种 dp 相结合的题目了。
从反面考虑,答案 \(=\) 总方案数 \(-\) 不包含任何一个 \(s_i\) 的方案数。
总方案数很简单,就是 \(26^n\),考虑计算不存在任何一个字符串 \(\in S\) 的方案数。
建出 AC 自动机,设 \(dp_{i,j}\) 表示填好 \(i\) 个字符,当前走到 AC 自动机 \(j\) 号节点的方案数。
显然如果 \(j\) 或 \(j\) 在 fail 树上某个祖先是字符串的末尾就不合法。
转移就从 \(j\) 向 \(j\) 的 \(26\) 个合法的儿子转移就行了。
复杂度 \(\mathcal O(26nm|s|)\)
洛谷 P2444 [POI2000]病毒
对所有病毒串建 AC 自动机。
考虑什么情况下会输出 TAK,如果你从某个点出发,沿着合法的点走了一圈又回到了当前点,那么就会输出 TAK。
也就是扣除不合法的点后,存在一个根节点能够到达的环,就输出 TAK。
暴搜记环即可。
洛谷 P3311 [SDOI2014] 数数
AC 自动机与数位 dp 的结合。
\(dp_{i,j,k}\) 表示填了 \(i\) 位,当前走到 AC 自动机上节点 \(j\) ,当前是否达到上界的情况为 \(k\) 的方案数。
枚举儿子转移即可。
但是这题有个比较烦的地方,就是 \(s_i\) 中可能含前导零。也就是说,你 \(dp\) 的时候有无前导零会对 \(dp\) 值产生影响。
不过有补救方法。假设 \(n\) 有 \(x\) 位,那么你可以求出有多少个满足条件的 \(1,2,3,\dots,x-1\) 位数——显然 \(n\) 的限制对它们没有影响。具体来说,你设 \(f_{i,j}\) 表示填了 \(i\) 位走到了 \(j\) 的方案数。\(dp\) 的时候你就钦定原数的第一位非零即可。
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int MAXL=1500;
const int ALPHA=10;
const int MOD=1e9+7;
char s[MAXL+5],buf[MAXL+5];bool mark[MAXL+5];
int n,ch[MAXL+5][ALPHA+1],ncnt=0,fail[MAXL+5];
int dp[MAXL+5][MAXL+5],f[MAXL+5][MAXL+5][2];
void insert(char *s){
int len=strlen(s+1),cur=0;
for(int i=1;i<=len;i++){
if(!ch[cur][s[i]-'0']) ch[cur][s[i]-'0']=++ncnt;
cur=ch[cur][s[i]-'0'];
} mark[cur]=1;
}
void getfail(){
queue<int> q;
for(int i=0;i<ALPHA;i++) if(ch[0][i]) q.push(ch[0][i]);
while(!q.empty()){
int x=q.front();q.pop();
for(int i=0;i<ALPHA;i++){
if(ch[x][i]) fail[ch[x][i]]=ch[fail[x]][i],q.push(ch[x][i]);
else ch[x][i]=ch[fail[x]][i];
}
}
}
int hd[MAXL+5],to[MAXL+5],nxt[MAXL+5],ec=0;
void adde(int u,int v){to[++ec]=v;nxt[ec]=hd[u];hd[u]=ec;}
void dfsfail(int x){for(int e=hd[x];e;e=nxt[e]) mark[to[e]]|=mark[x],dfsfail(to[e]);}
void add(int &x,int y){x+=y;if(x>=MOD) x-=MOD;}
int main(){
scanf("%s%d",s+1,&n);int len=strlen(s+1);
for(int i=1;i<=n;i++) scanf("%s",buf+1),insert(buf);
getfail();for(int i=1;i<=ncnt;i++) adde(fail[i],i);dfsfail(0);
for(int i=1;i<ALPHA;i++) if(!mark[ch[0][i]]) add(dp[1][ch[0][i]],1);
for(int i=1;i<len-1;i++) for(int j=0;j<=ncnt;j++) for(int k=0;k<ALPHA;k++)
if(!mark[ch[j][k]]) add(dp[i+1][ch[j][k]],dp[i][j]);
int ans=0;
for(int i=1;i<len;i++) for(int j=0;j<=ncnt;j++) add(ans,dp[i][j]);
for(int i=1;i<=s[1]-'0';i++) if(!mark[ch[0][i]]) add(f[1][ch[0][i]][i==(s[1]-'0')],1);
for(int i=1;i<len;i++) for(int j=0;j<=ncnt;j++) for(int k=0;k<2;k++){
int up=(k)?(s[i+1]-'0'):9;
for(int l=0;l<=up;l++) if(!mark[ch[j][l]]) add(f[i+1][ch[j][l]][k&&(l==(s[i+1]-'0'))],f[i][j][k]);
}
for(int i=0;i<=ncnt;i++) add(ans,f[len][i][0]),add(ans,f[len][i][1]);
printf("%d\n",ans);
return 0;
}
洛谷 P3041 [USACO12JAN]Video Game G
常规题,和 P4052 基本一致,不赘述了。
Codeforces 1202E You Are Given Some Strings...
考虑转化贡献体,对于每个 \(s_i+s_j\) 在原串中出现的位置,都会存在一个分割点 \(x\),它左边是 \(s_i\),右边是 \(s_j\)。
于是我们可以枚举分割点 \(x\),假设有 \(c1\) 个字符串的结尾为 \(x\),有 \(c2\) 个字符串开头是 \(x+1\),那么根据乘法原理,这会对答案产生 \(c1\times c2\) 的贡献。
那么怎么求出 \(c1,c2\) 呢?求 \(c1\) 很简单,AC 自动机直接跑一遍就行了。求 \(c2\) 可以把所有 \(s_i\) 和文本串都反过来,然后跑一遍 AC 自动机就可以了。复杂度线性。
洛谷 P3715 [BJOI2017]魔法咒语
众所周知,北京省选的日常就是数据分支。
\(L \leq 100\) 的非常容易,感觉和 P4052 也没多大区别。
下面着重考虑 \(L \leq 10^8\) 的情况,基本词汇长度不超过 \(2\)。
先考虑基本词汇长度都为 \(1\) 的情况。转移方程式可以写成 \(dp_{i+1,y}+=dp_{i,x}\) 的形式,这时候你可以很自然地想到矩阵快速幂。如果从 AC 自动机上某个合法的点 \(x\) 可以到达另一个合法的点 \(y\),就令矩阵第 \(x\) 行第 \(y\) 列的值 \(+1\)。再用一个向量维护 \(dp_{i,0},dp_{i,1},\dots\) 的值就可以了。
接下来再考虑基本词汇长度不超过 \(2\) 的情况。这时候转移方程式会出现 \(dp_{i+2,y}+=dp_{i,x}\) 的情况。考虑将矩阵的大小 \(\times 2\)。用一个 \(2n\) 的向量维护 \(dp_{i-1,0},dp_{i-1,1},\dots,dp_{i,0},dp_{i,1},\dots\) 的值。
那么怎样从 \(dp_{i-1,0},dp_{i-1,1},\dots,dp_{i,0},dp_{i,1},\dots\) 转移到 \(dp_{i,0},dp_{i,1},\dots,dp_{i+1,0},dp_{i+1,1},\dots\) 呢?对于 \(dp_{i,0},dp_{i,1},\dots\) 显然可以直接从前一向量继承过来,于是转移矩阵第 \(i+n\) 行第 \(i\) 列的值均为 \(1\)。接下来考虑 \(dp_{i+1,y}\) 怎样得到;对于可以从 \(dp_{i-1,x}\) 转移到 \(dp_{i+1,y}\) 的 \(x\),在转移矩阵第 \(x\) 行 \(y+n\) 列 \(+1\),表示 \(dp_{i+1,y}\) 由 \(dp_{i-1,x}\) 得到;对于可以从 \(dp_{i,x}\) 转移到 \(dp_{i+1,y}\) 的 \(x\),在转移矩阵第 \(x+n\) 行 \(y+n\) 列 \(+1\),表示 \(dp_{i+1,y}\) 由 \(dp_{i,x}\) 得到。然后和刚才一样跑矩阵快速幂即可。
Codeforces 710F String Set Queries
非常规 AC 自动机套路题,题解
总结
AC 自动机的内容就到此为止了。这类题目题目大体可分为三类:与 \(dp\) 相结合,与树相结合,以及其它。当碰到多模式串匹配的问题的时候,就可以往这方面想。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号