推荐

粗排

精排

粗排和精排的一致性

参考资料：https://www.zhihu.com/question/554471691/answer/3175633203

具体而言，精排模型的训练样本来自于曝光、点击等行为日志。在推荐场景下，能够得到曝光的物品是经过了召回、粗排之后，并且经过了线上的精排模型筛选之后的物品。这些物品是与当前用户的兴趣最可能匹配的集合。因此，精排模型的任务是从“最可能匹配用户兴趣”的集合中挑选出“确实匹配用户兴趣”的物品，即那些用户愿意与之发生正向行为的物品，并且按照意愿的强烈程度排好序

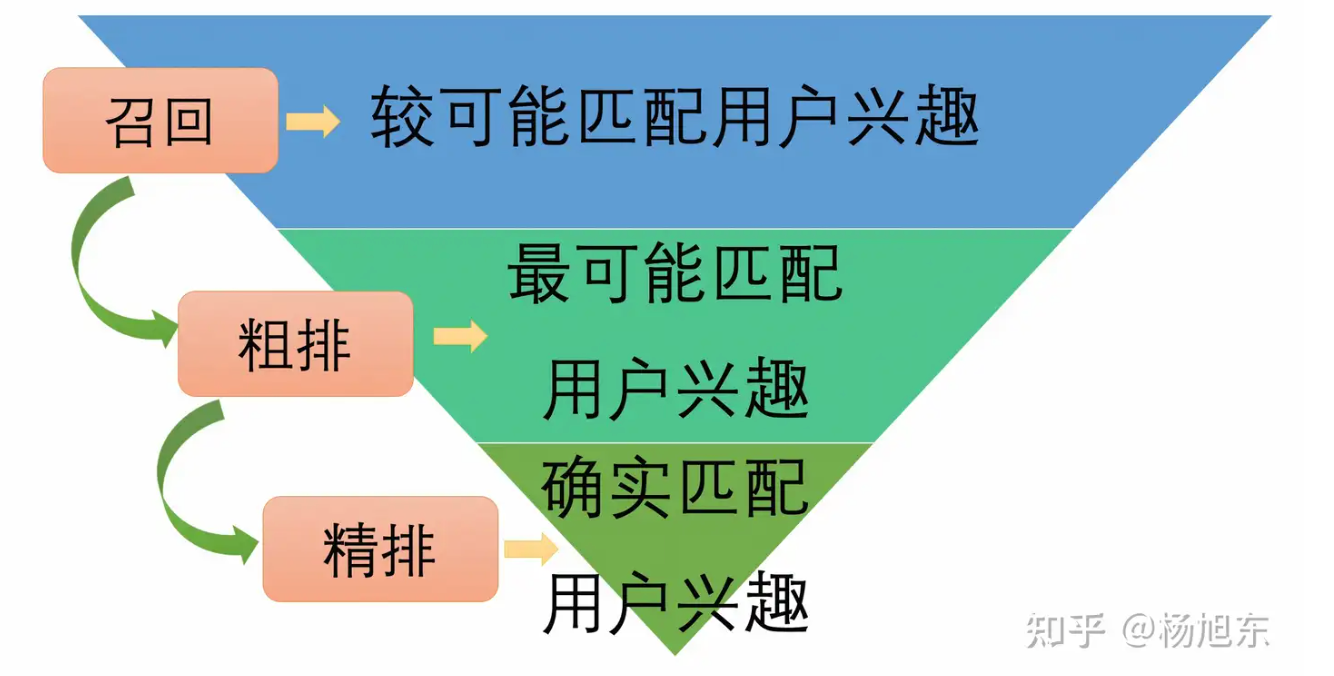
因此，精排模型的训练样本来自于一个叫做“最可能匹配用户兴趣”的数据分布；粗排模型的训练样本来自于一个叫做“比较可能匹配用户兴趣”的数据分布。这两个数据分布是不同的，所以直接把精排模型当作粗排模型来用，让它在推理阶段接受很多在训练时从未见过的样本（从特征向量的角度），本质上在一定程度上违反了机器学习的前提条件：独立同分布假设。因而，效果不理想也就可以理解了。精排放量其实也是同样的道理。

预估值校准

负采样导致的校准

参考资料：https://www.bilibili.com/video/BV19t4y1p7UM/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=a70439aae0ce70e41b5fe1a6dc35d6c8

模型训练可能会遇到类别不平衡的困难。可以通过负样本降采样(down-sampling)，保留一小部分负样本。同时也能让让正负样本数量平衡，节约计算。但是会出现CTR预估不准确的情况。

正样本、负样本数量为 \(n_+\) 和 \(n_-\)。对负样本做降采样，抛弃一部分负样本。使用 \(\alpha \cdot n_-\) 个负样本， \(a\in (0,1)\) 是采样率。由于负样本变少，预估点击率大于真实点击率

真实点击率： \(p_\text{true}=\frac{n_+}{n_++n_-}\) ，预估的点击率 \(p_\text{pred}=\frac{n_+}{n_++\alpha \cdot n_-}\) ，校准公式如下：

\[p_\text{true}=\frac{\alpha\cdot p_\text{pred}}{(1-p_\text{pred}) + \alpha \cdot p_\text{pred}} \]

保序回归

参考资料：

• https://www.woshipm.com/pd/5843246.html

• https://blog.csdn.net/weixin_42468475/article/details/115319437

• https://www.xzywisdili.com/post/2023-03-07-isotonicregression/

方法二：保序回归

保序回归法目前是业界最常用的校准方法。常见的算法是保序回归平滑校准算法（Smoothed Isotonic Regression，SIR）。整体执行步骤如下：

Step1—区间分桶

首先将 Pctr 值从小到大进行排序，然后按照区间分为 K 个桶。假设我们分为 100 个桶：(0,0.01], (0.01,0.02], (0.02,0.03],…, (0.99,1]。这里我们认为精排模型给出的 Pctr 值是具有参考意义的，同一个区间里的 PV 请求具有近似的真实点击率，每一个区间可作为一个合理的校准维度（分簇维度）。然后实际应用时，我们再统计每一个桶里的后验 CTR 值。比如今天线上一共有 1000 次预估的 Pctr 落在了桶 (0.02,0.03] 之间，然后我们统计这 1000 个预估的后验 CTR，假设后验 CTR 为 0.23%。关于每个桶里 Pctr 和 Actr 平均值的计算公式如下：

Step2—桶间合并

如果说后验 CTR 的值超出了对应分桶的 PCTR 取值区间怎么办？假如原本分桶在 (0.02,0.03] 之间结果的后验 CTR 为 3.5%，这时已经进入到了下一个桶里了 (0.03,0.04]。如果我们将原本 Pctr 在(0.02,0.03] 桶里面的值往下一个桶里的区间值进行校准，这就破坏了原有桶之间的顺序，保序回归的基本逻辑是不能破坏原有 Pctr 的顺序。此时我们需要把 (0.02,0.03] 和(0.03,0.04]桶进行合并得到新的桶（0.02,0.04]，再重新对落入两个桶里的数据进行后验 CTR 统计，得到新桶里面的 Actr 和 Pctr 平均值。我们以 Pctr 为 x 轴，Actr 为 y 轴，最终得到一个如下图所示单调递增的散点图：

Step3—桶间插值分段校准

我们需要基于上述散点图去构造一个校准函数，输入 x 值以后就可以输出校准后的 y 值。如果直接拟合一个 y = kx + b 函数，最终预估的结果不够平滑。目前业界的标准做法都是构造分段校准函数。

如上图所示，我们将两个桶之间坐标点连接起来，然后去构造一个分段的 y = kx + b 校准函数，假设 Pctr 一共分为了 100 个桶，那么最终就构造 100 个分段校准函数，这样既保证单调性，又保证平滑地校准。分段的校准函数如何得出，这里就是基础的初中数学知识，已知两点坐标计算对应的 y = kx + b。

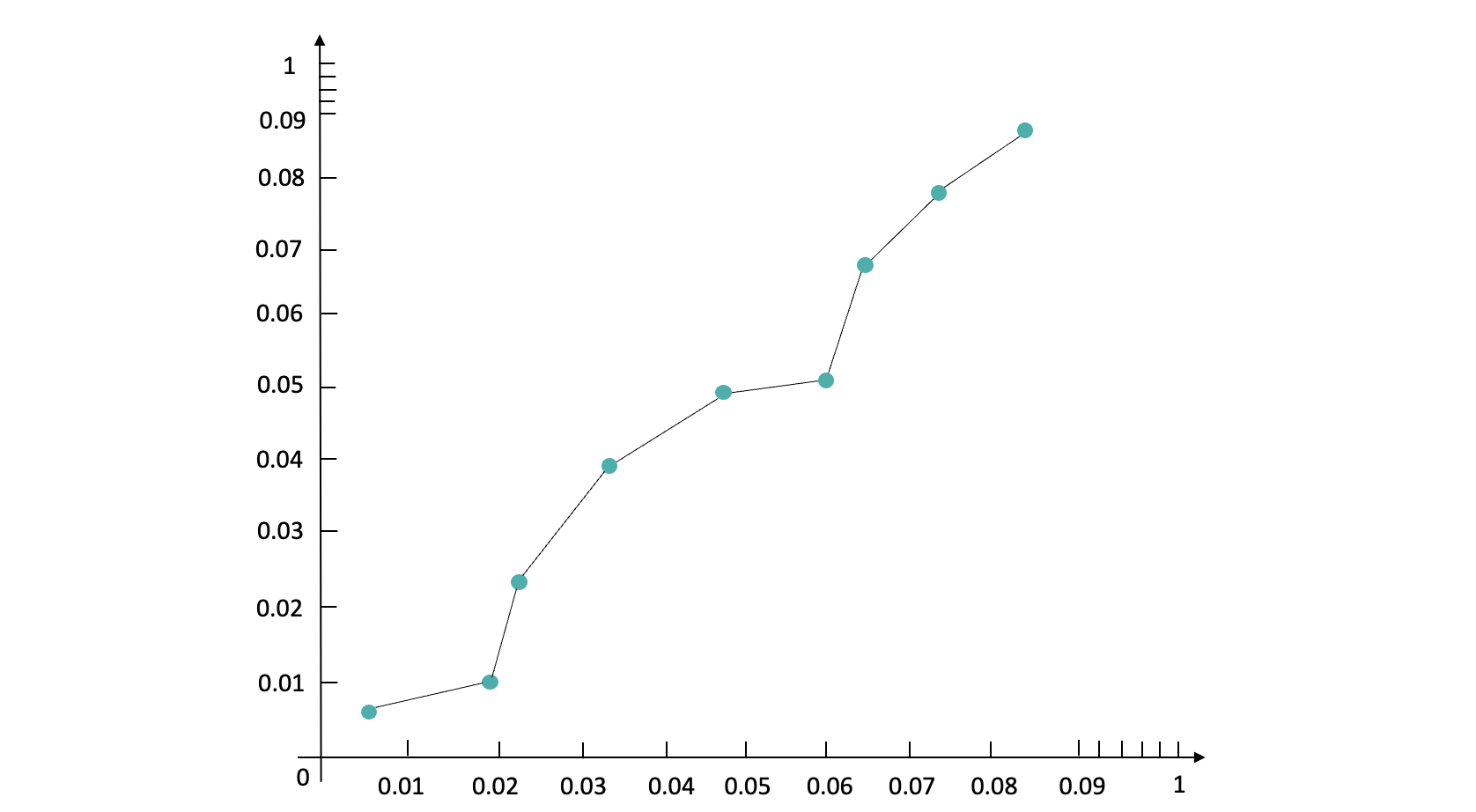
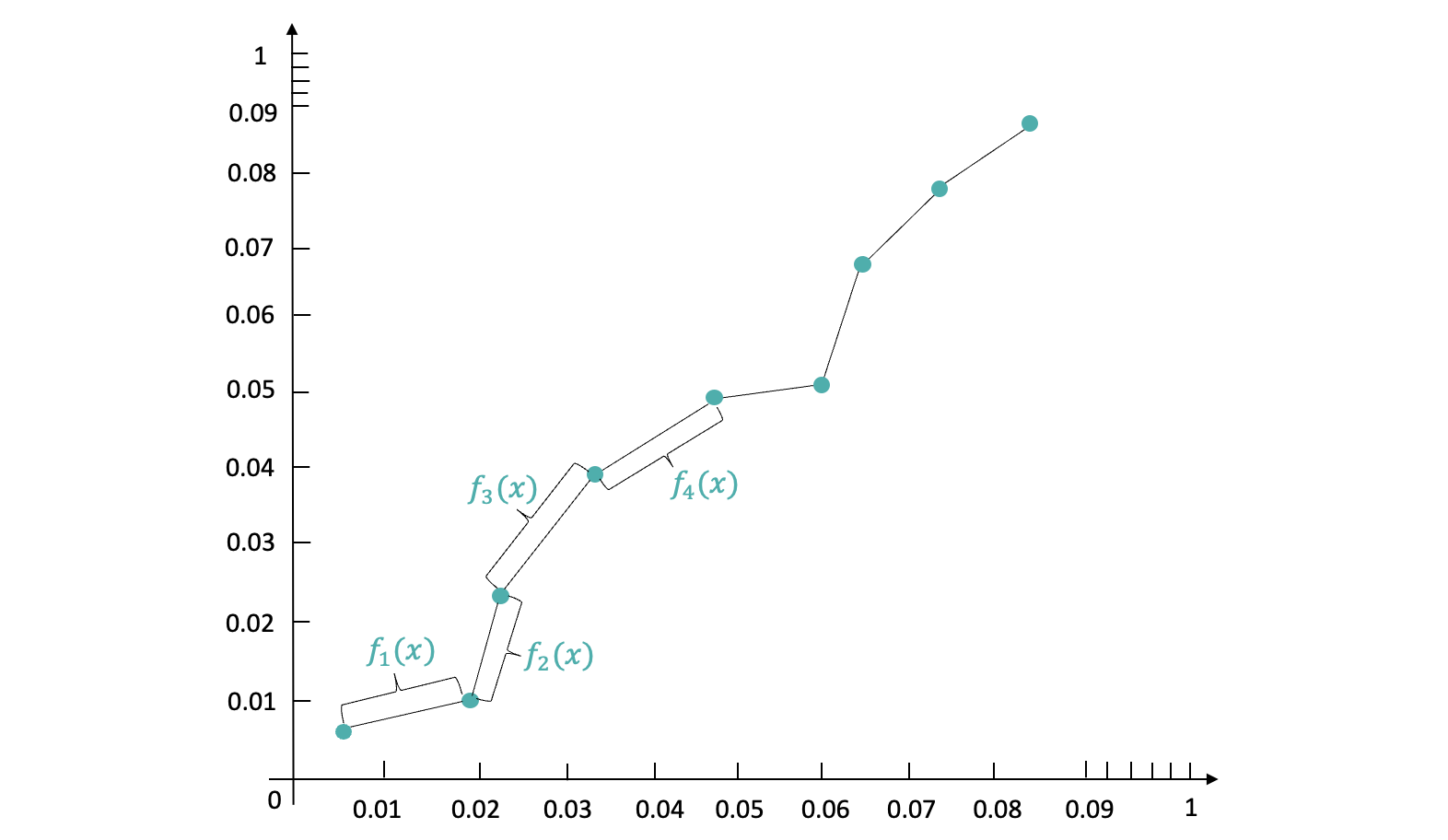
保序回归法的整体思想就是：不改变原有数据的 Pctr 排序，仅在原有 Pctr 的排序上进行纠偏。最终纠偏出来的 CTR 数据分布的单调性不变，AUC 指标不变。

本身因为特征选择和样本采样导致的 CTR 偏差，需要基于先验知识的特征调整和基于负样本采样率的方法来对 CTR 进行纠偏。如果精排模型输出的 Pctr 和 Actr 差异很大，这种是无法依靠校准模块来进行纠偏的。

PAVA 算法

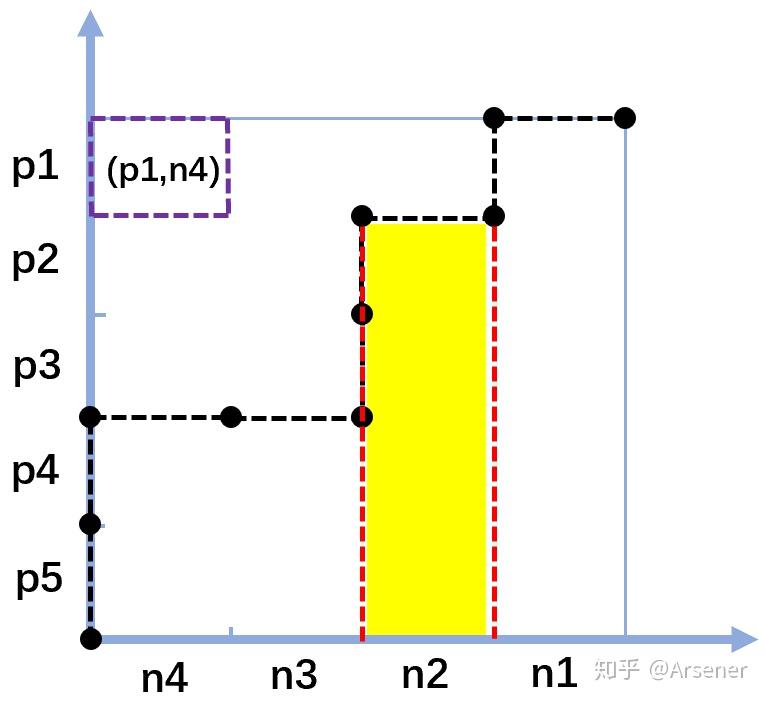
求解保序回归的一种最常用算法是 PAVA 算法（ Pool-Adjacent-Violators Algorithm，池相邻违规者算法）。PAVA 算法的直观形式只需要看下面这张图就行了：

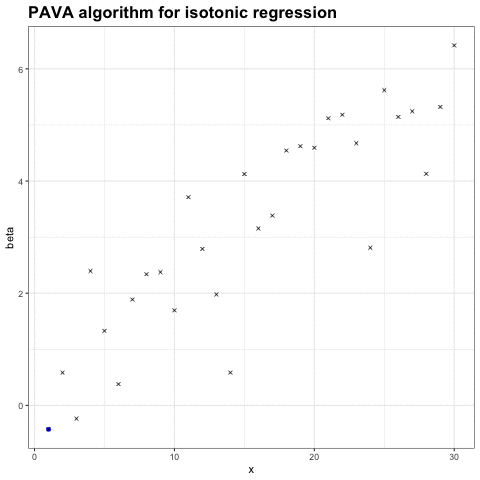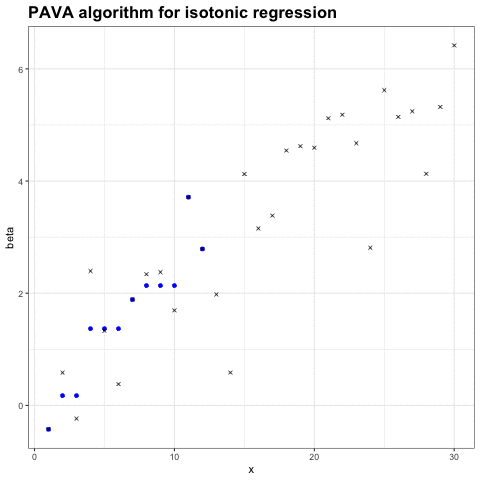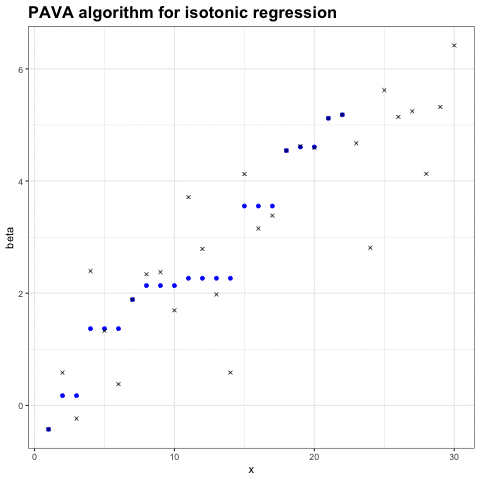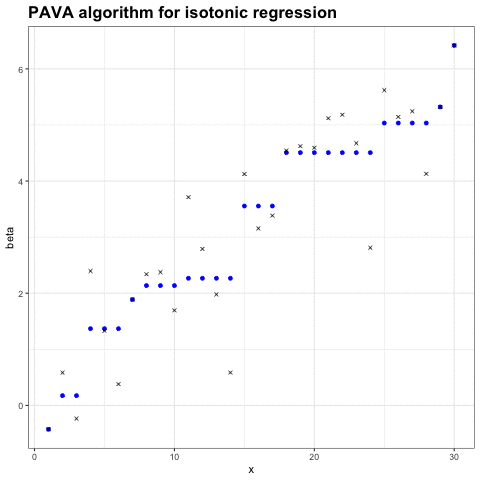
这种算法是通过从左往右逐渐扫描数据序列，并且保证整个序列是单调递增的，以此来获得 Beta 值的结果。如果 Beta_i < Beta_i-1，那么就同时把这两个值替换为 (Beta_i + Beta_i-1) / 2。以此就能获得严格且平滑的保序回归。

通过 PAVA 算法，可以获得一个包括多个 Beta 参数组成的单调递增序列，用可视化的方法可以看到是由多条上升线和水平线组成的函数图：

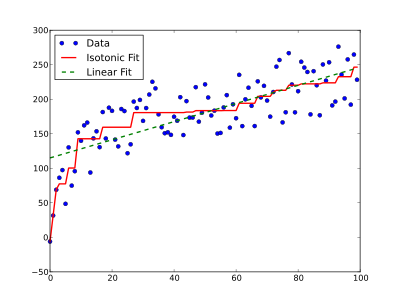
SSB问题

CVR的SSB问题

业界在训练转化率（CVR）预估模型时，所采用数据集的正负样本分别为：点击未转化为负样本，点击转化为正样本。也就是整个样本集都是在有点击的样本上构建的。但在做在线infer时，是对整个样本空间进行预估，这就导致了样本选择偏差问题（即在离线样本空间有gap）。

ESMM让cvr任务打平了ctr任务，变成了在整个有曝光的样本空间上进行训练。

粗排的SSB问题

参考资料：https://zhuanlan.zhihu.com/p/574752588?utm_id=0

对精排排序靠后的样本进行负采样。

PLE

参考资料：https://blog.csdn.net/u012328159/article/details/123617326

动机

说到动机，先来说说多任务学习领域中存在的两大问题：

负迁移（negative transfer）：MTL提出来的目的是为了不同任务，尤其是数据量较少的任务可以借助transfer learning（通过共享embedding，当然你也可以不仅共享embedding，再往上共享基层全连接网络等等这些很常见的操作）。但经常事与愿违，当两个任务之间的相关性很弱（比如一个任务是判断一张图片是否是狗，另一个任务是判断是否是飞机）或者非常复杂时，往往发生负迁移，即共享了之后效果反而很差，还不如不共享。

跷跷板现象：还是当两个task之间相关性很弱或者很复杂时，往往出现的现象是：一个task性能的提升是通过损害另一个task的性能做到的。这种现象存在很久，PLE论文里给它起了个非常贴切的名字『跷跷板』，想象一下你小时候玩跷跷板的情形吧，胖子把瘦子跷起来。

PLE模型细节

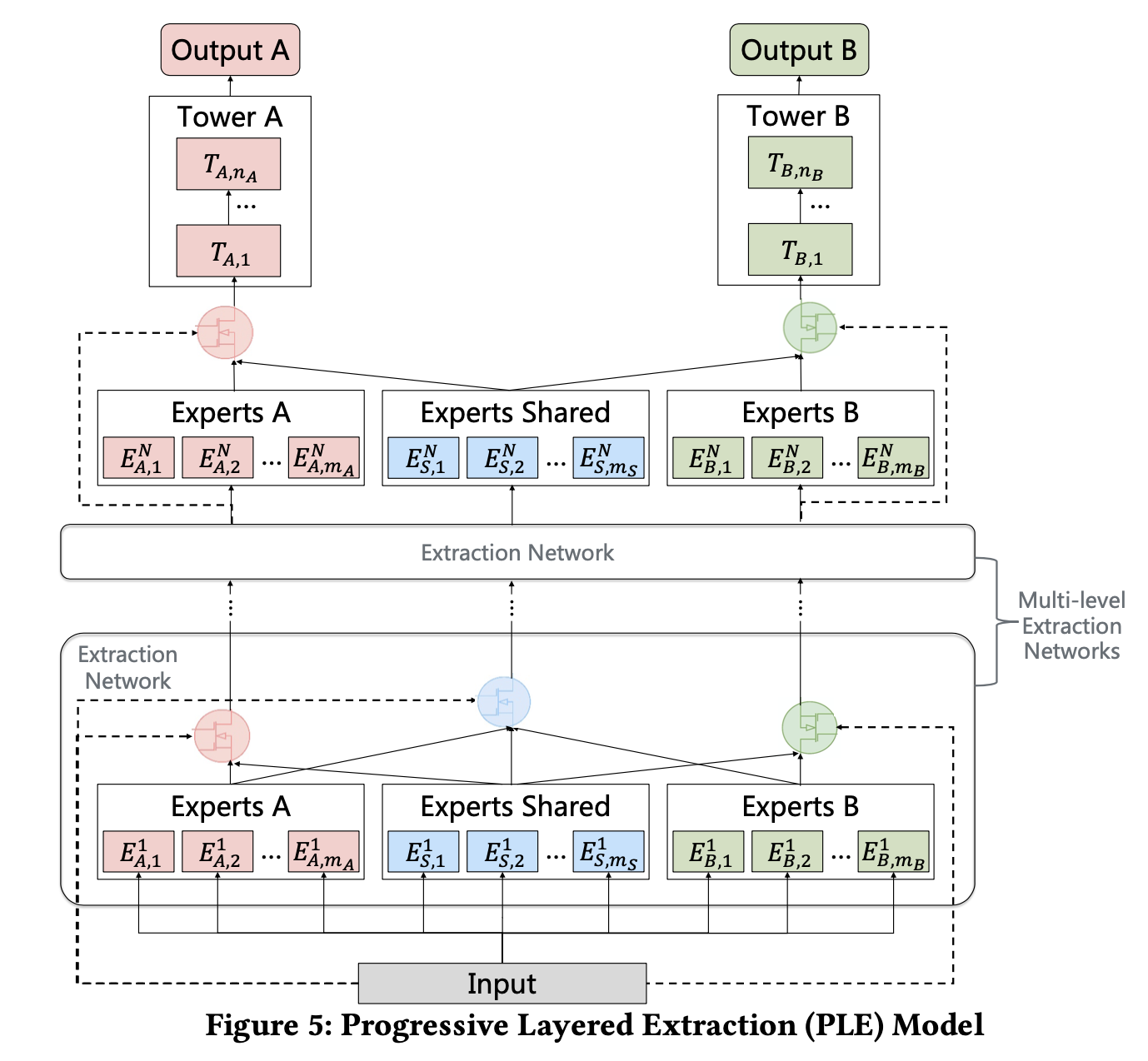
先来从整体上看看这个模型，大家自行对比下 MMoE（参见博客推荐系统（十五）多任务学习：谷歌 MMoE（Multi-gate Mixture-of-Experts ）），可能就能体会到我前面说 PLE 性能提升更像是复杂参数所带来的这句话了，因为粗略的看，PLE 做了 deep 化（expert 完后再来一层 expert），显然要比浅层的效果来得好。

我们来自底向上的拆解下 PLE：

Extraction Network

PLE 这里相比较 MMoE 做了比较大的创新，在 MMoE 里，不同 task 通过 gate（网络）共享相同的 expert（网络），而 PLE 中则把 expert 分为了两种：共享的 expert（即上图中的 experts Shared）和每个 task 单独的 expert（task-specific experts）。因此，这种设计既保留了 transfer learning（通过共享 expert）能力，又能够避免有害参数的干扰（避免 negative transfer）。

同样的，在 gate 网络部分，也分为了 task-specific 和 Shared，以上图左边的这个 gate（即上图中红色的 gate）为例，它的输入有两部分，分别为 Experts A 和 Experts Shared。而 shared gate（上图中蓝颜色的 gate）的输入则为三部分：Experts A、Experts Shared 和 Experts B。最终三部分直接作为下一层的输入，分别对应到下一层的 Experts A、Experts Shared 和 Experts B。有一说一，图 figure5 如果把中间那个 extraction network 去掉，会更加清晰。算了，原来想偷个懒，不想画图的，我还是上个简化版的图吧。

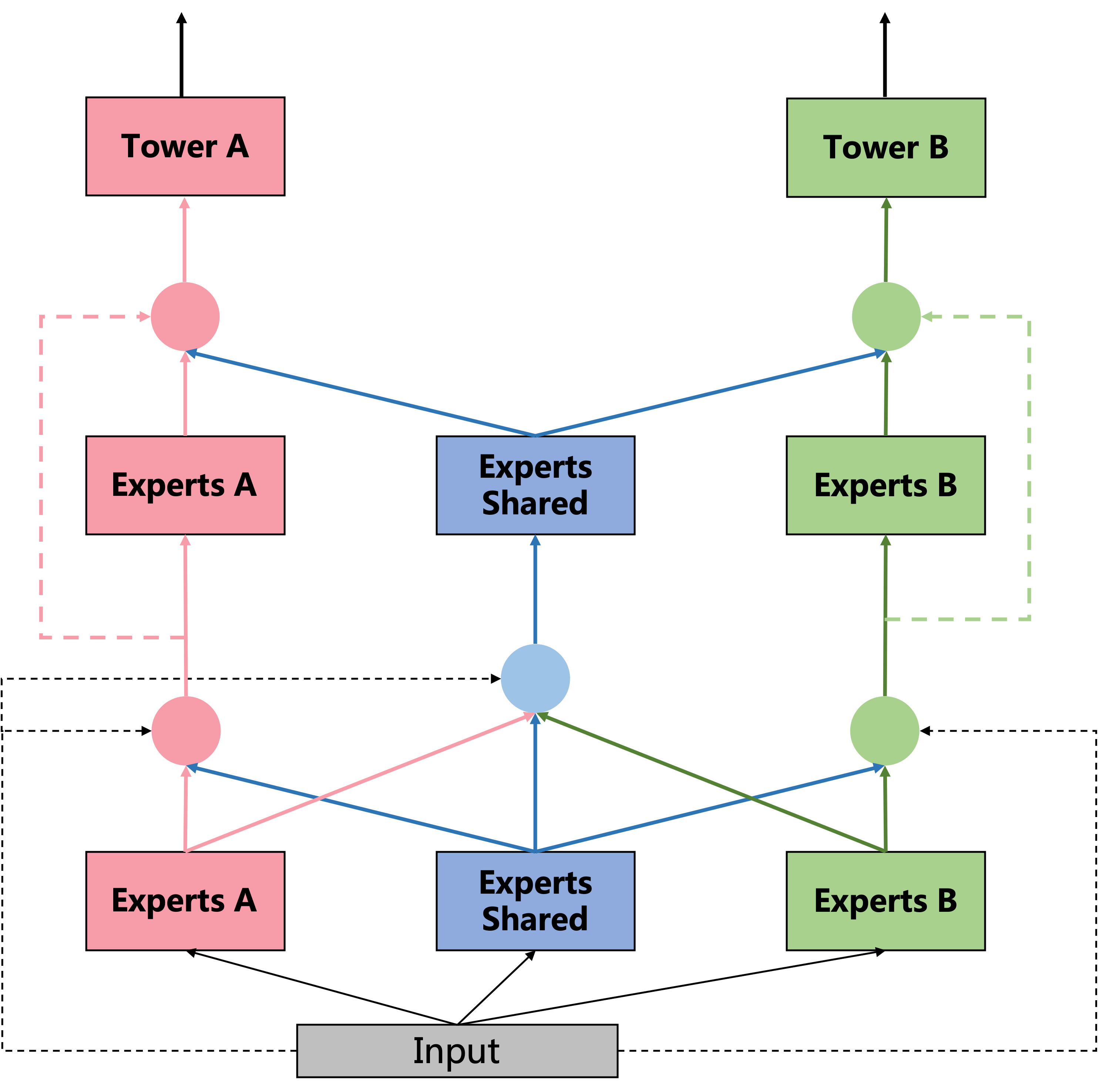
图 3. PLE 模型简化版

再来总结下一些细节，有助于我们代码实现。

1. Gate 网络的数量取决于 task 数量，第一层由于多了个 shared gate，所以数量等于 task 数量 + 1，第二层 gate 网络数量与 task 数量相同。Gate 网络最后一层全连接层的隐藏单元（即输出）size 必须等于 expert 个数。另外，Gate 网络最后的输出会经过 softmax 进行归一化。
2. gate 网络作用机制与 MMoE 相同，以 task A 为例：输出维度（假设为 \((g_1, g_2, g_3, g_4, g_5)\) 等于 expert 数量 (3 个 task-specific expert，2 个 shared expert)，意味着 \(g_1\) 广播作用于 \(expert_1\) 的每一个输出元素上， \(g_2\) 广播作用于 \(expert_2\) 的每一个输出元素上，以此类推。然后把每一个 expert 输出向量做 element-wise add，即对应位置元素想加，最终得到第二层的 expert A。 此外，第二层的 Expert shared 由第一层全部的 expert 做 element-wise add 得到。（建议结合上图理解）
3. 每个 task 的 expert 数量以及 shared expert 是个超参，比如最后 paddle 代码里，每个 task 有 3 个 expert，shared expert 数量为 2。实际上每个 task 的 expert 数量为 3+2=5。
4. 相比较 MMoE，PLE 除了做了一些创新后，网络结构上深度变深了，变成了 2 层，这也是为什么我说性能提升像是通过增加参数带来的。
5. PLE 第二层 gate 网络数量与 task 数量相同，第一层多了一个 shared gate。

其他一些细节

• 腾讯视频 rerank 模块的公式为：

  \[score={P_{VTR}}^{W_{VTR}} \times {P_{VCR}}^{W_{VCR}} \times {P_{SHR}}^{W_{SHR}} \times ... \times{P_{CMR}}^{W_{CMR}} \times f(video\_len) \]

  其中，VCR（View Completion Ratio）为视频观看完成率，VTR（View- Through Rate）为视频是否为有效观看，CMR（Comment Rate）为评论率，SHR（Share Rate）为分享率。 \(W\) 为权重因子，用于调整每个指标的权重。

• 关于 loss 函数，每个 task 的 loss 加了个可学习的权重参数 \(w\) ，用于模型自动学习每个 task 的 loss 的权重。

MMOE

参考资料：https://blog.csdn.net/u012328159/article/details/123309660

动机

说到动机，自然就要先说当前现状存在的问题。目前在MTL领域存在的问题：

工业界真实场景下，多个任务之间的相关性并不是很强，这个时候如果再用过去那种共享底座embedding的结构，往往会导致『跷跷板』现象。

当前学术界已经有很多工作意识到1中描述的问题并且尝试去解决，但大多数工作的套路都是『大力出奇迹』的路子，即加很多可学的参数去学习多个任务之间的difference，这在学术界跑跑数据，写写论文倒是没什么，但是在工业界场景下，增加这些参数会导致线上做infer时耗时增加，导致模型服务可用性大大下降，这是无法接受的。

MMoe模型结构

关于MMoe的模型结构，先上个论文中的原图：

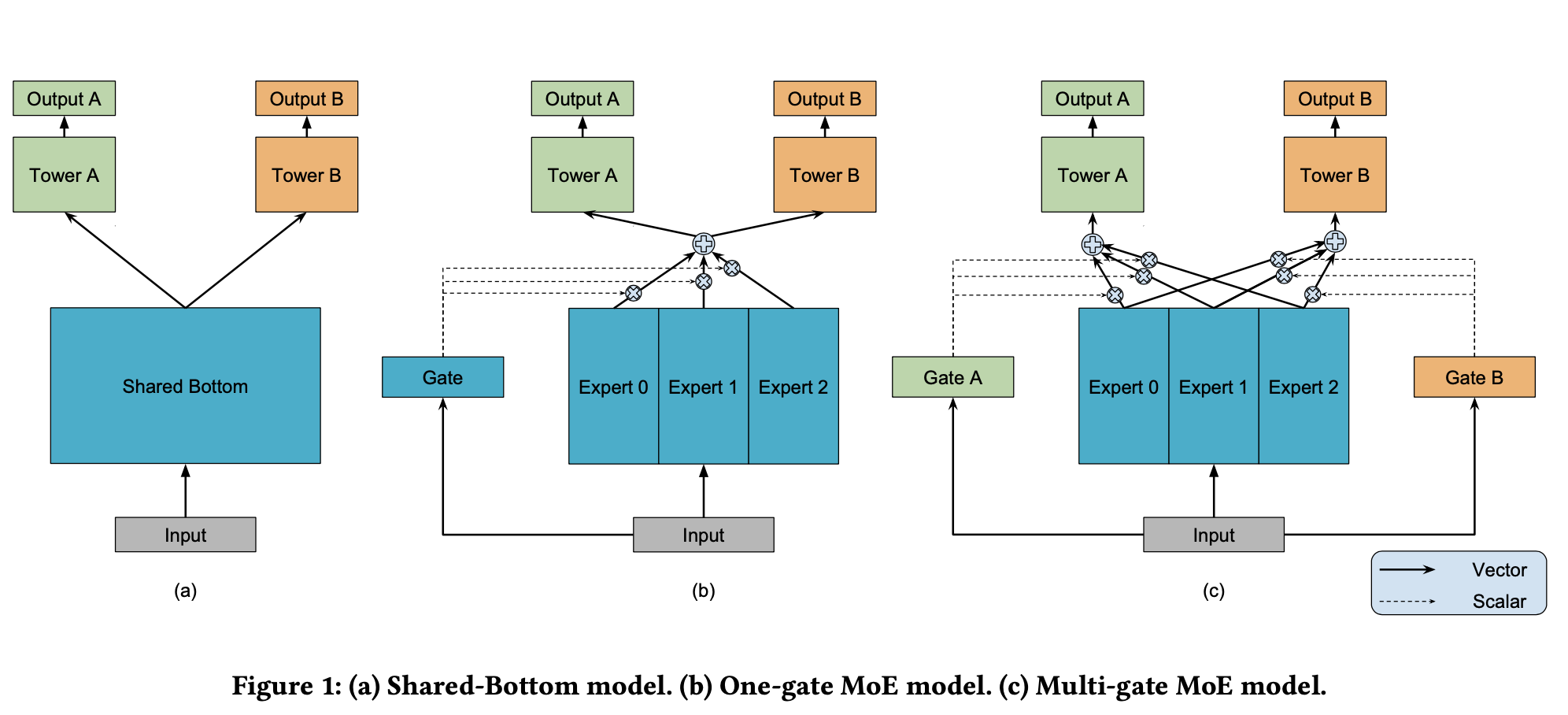
图中（a）展示了传统的MTL模型结构，即多个task共享底座（一般都是embedding向量），（b）则是论文中提到的一个gate的Mixture-of-Experts模型结构，（c）则是论文中的MMoE模型结构。

我们重点来看下MMoE结构，也就是图1 ( c )，这里每一个expert和gate都是一个全连接网络（MLP），层数由在实际的场景下自己决定。下面上一个我画的详细版本的MMoE模型结构图，有了这个图，公式都不用了，直接对着图代码实现就可以了。

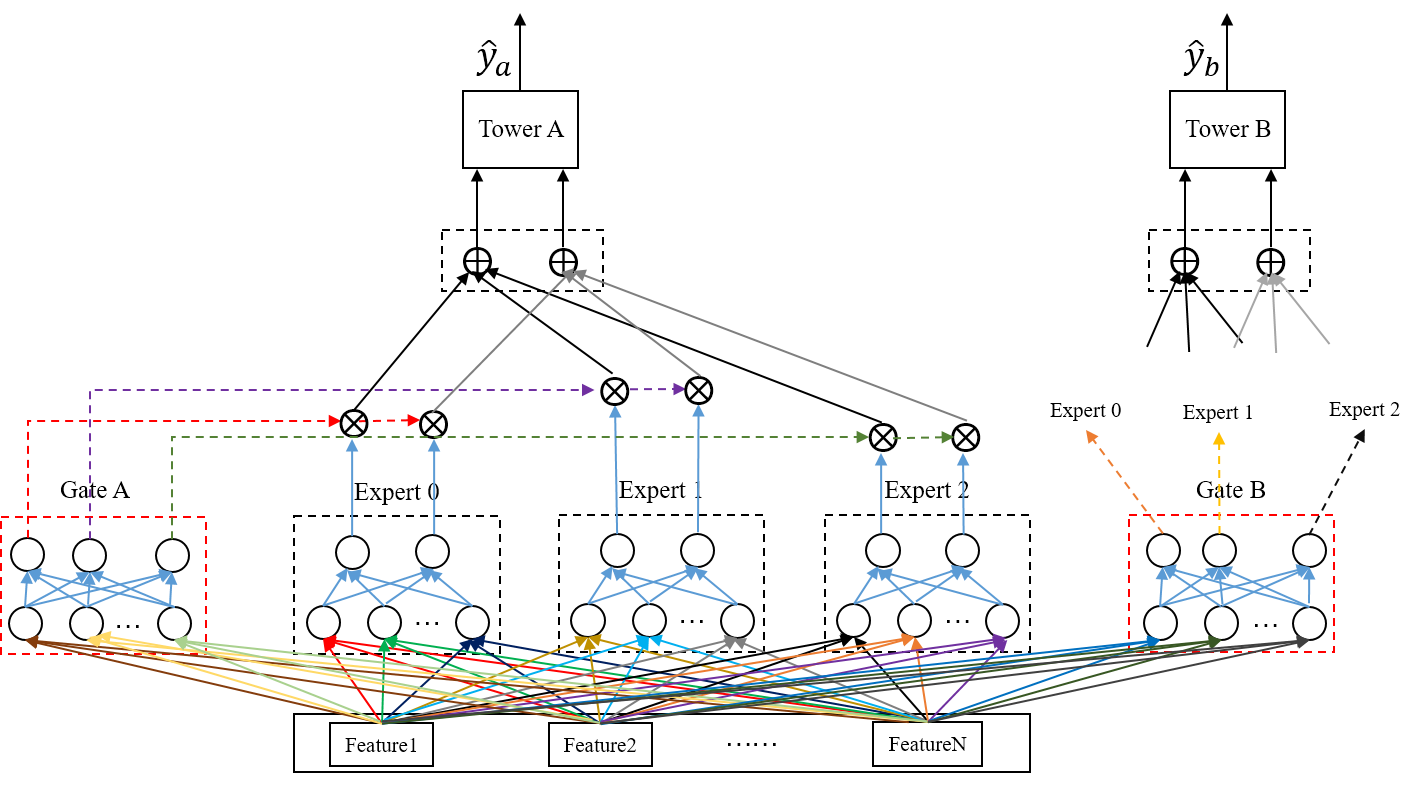
注：GateB 那部分没画出来，因为画出来会显得很乱，参考 GateA 即可。

从上图 2 中，我们可以出来几个细节（一定要仔细看，非常重要！！！）：

1. Gate 网络的数量取决于 task 数量，即与 task 数量相同。Gate 网络最后一层全连接层的隐藏单元（即输出）size 必须等于 expert 个数。另外，Gate 网络最后的输出会经过 softmax 进行归一化。
2. Gate 网络最后一层全连接层经过 softmax 归一化后的输出，对应作用到每一个 expert 上（图 2 中 GateA 输出的红、紫、绿三条线分别作用与 expert0，expert1，expert2），注意是通过广播机制作用到 expert 中的每一个隐藏单元，比如红线作用于 expert0 的 2 个隐藏单元。这里 gate 网络的作用非常类似于 attention 机制，提供了权重。
3. 假设 GateA 的输出为 \([GA_1, GA_2, GA_3]\) ，expert0 的输出为 \([E0_1, E0_2]\) ，expert1 的输出为 \([E1_1, E1_2]\) ，expert2 的输出为 \([E2_1, E2_2]\) 。GateA 分别与 expert0、expert1、expert2 作用，得到 \([GA_1*E0_1, GA_1*E0_2], [GA_2*E1_1, GA_2*E1_2], [GA_3*E2_1, GA_3*E2_2]\) ，然后对应位置求和得到 towerA 的输入，即 towerA 的输入 size 等于 expert 输出隐藏单元个数（在这个例子中，expert 最后一层全连接层隐藏单元个数为 2，因此 towerA 的输入维度也为 2），所以 towerA 的输入为 $[GA_1E0_1+GA_2E1_1+GA_3E2_1, GA_1E0_2+GA_2E1_2+GA_3E2_2] $ 。
4. expert 每个网络的输入特征都是一样的，其网络结构也是一致的。
5. 两个 gate 网络的输入也是一样的，gate 网络结构也是一样的。

一直觉得举例子画图胜过任何繁琐复杂的解释，有了上面那个例子，相信大家基本上看完一遍就理解整个 MMoE 的精髓了。

1. 疑问点1
   【问】： expert网络结构一样，输入特征一样，是否会导致每个expert学出来的参数趋向于一致，从而失去了ensemble的意义？
   【答】： 在网络参数随机初始化的情况下，不会发生问题中提到的问题。核心原因在于数据存在multi-view，只要每一个expert网络参数初始化是不一样的，就会导致每一个expert学到数据中不同的view（paddle官方实现就犯了这个致命错误）。微软的一篇论文中提到因为数据存在multi-view，训练多个DNN时，即使一样的特征，一样的超参数，只要简单的把参数初始化设置不一样， 这多个DNN也会有差异。论文参见：Towards Understanding Ensemble, Knowledge Distillation, and Self-Distillation in Deep Learning
   所以大家在实现的时候，一定要注意这一个点，只需要简单的把参数初始化设置为随机即可。

2. 疑问点2
   【问】： 是否应该强上MTL？
   【答】： 如果task之间的相关性很弱，基本上都会发生negative transfer，所以MTL是绝对打不过single model的，不要盲目的为了显得高大上牛逼哄哄的一股脑MTL。还是那句话，模型不重要，重要的是对数据及场景的理解。

极化现象

mmoe中的极化现象是指在mmoe的gate中，对于有些任务可能会出现某个专家的权重很大，而其他的专家权重很小，也就是说该任务只会用到某一个专家网络的输出，无法使用到不同专家网络的信息。

极化有什么坏处？

• 任务之间的干扰，如果大家都走一个专家了，那相当于没有分专家，可以简化看作是共享层，不同的任务之间会存在干扰，也会受负迁移等影响
• 泛化能力下降，原因和上面类似

如何缓解mmoe中的极化现象？

• 正则化方法 ：在Gate中加入dropout，这也是youtube的论文中使用的方法，dropout可以随机忽略一部分神经元，缓解过拟合；也可以尝试BN，L2等正则化方法来防止出现极端值
• 缩放 ：对进入softmax之前的logit进行缩放，比如常见的除以维度中最大的logit来归一化
• 复杂网络 ：增加gate网络的层数等，构建更复杂的网络挖掘特征之间的关系

ESSM

参考资料：https://blog.csdn.net/u012328159/article/details/123309675?spm=1001.2014.3001.5501

动机

• 样本选择偏差：目前业界在训练转化率（CVR）预估模型时，所采用数据集的正负样本分别为：点击未转化为负样本，点击转化为正样本。也就是整个样本集都是在有点击的样本上构建的。但在做在线infer时，是对整个样本空间进行预估，这就导致了样本选择偏差问题（即在离线样本空间有gap）。

• 数据稀疏：用于cvr训练的都是有点击的样本，这部分样本实在是太少了，对于广告而言，大盘的点击率也就在2%左右，其中能够转化的更加少之又少（正样本）。所以在DL流行起来之前，这点样本量，基本上一个xbg之类的也就够了，后来有了DL之后，最多也就是用下MTL，也就是ctr和cvr共享底座embedding，这样cvr的embedding相对学习的比较充分。

  这一点上，ESMM倒没有什么创新，也是通过共享底座embedding的方式也减缓这种情况。

模型结构

CVR 模型的目的很明确，就是预估广告被点击之后的转化率（Post-Click Conversion Rate）

因此，cvr 模型训练的时候只能用有点击的样本，这也直接导致了在离线的样本选择偏差（SSB）。如果我们想在训练的时候把样本空间扩大到整个有曝光的样本，那么需要怎么办呢？现在很明确的是 CTR 任务是用全部有曝光的样本，ESMM 这里巧妙的做了转换，即训练 CTCVR 和 CTR 这两个任务，那么 CTCVR 和 CTR、CVR 之间的关系如何呢？下面就来看一下：

广告从 曝光 → 点击 → 转化 这条路面是有序的，假设我们用 x， y， z 来分别表示样本，是否点击，是否转化。那么，我们可以用公式形式化的表达为：

\[\underset{pCTVR}{\underbrace{p(y=1,z=1 | x)}} = \underset{pCTR}{\underbrace{p(y=1|x)}} \times \underset{pCVR}{\underbrace{p(z=1|y=1, x)}} \tag{1} \]

公式（1）清楚的表达了 CTCVR 与 CTR、CVR 之间的关系，有了这个关系就好办了，ESMM 的出发点就是：既然 CTCVR 和 CTR 这两个任务训练是可以使用全部有曝光样本的，那我们通过这学习两个任务，隐式地来学习 CVR 任务。

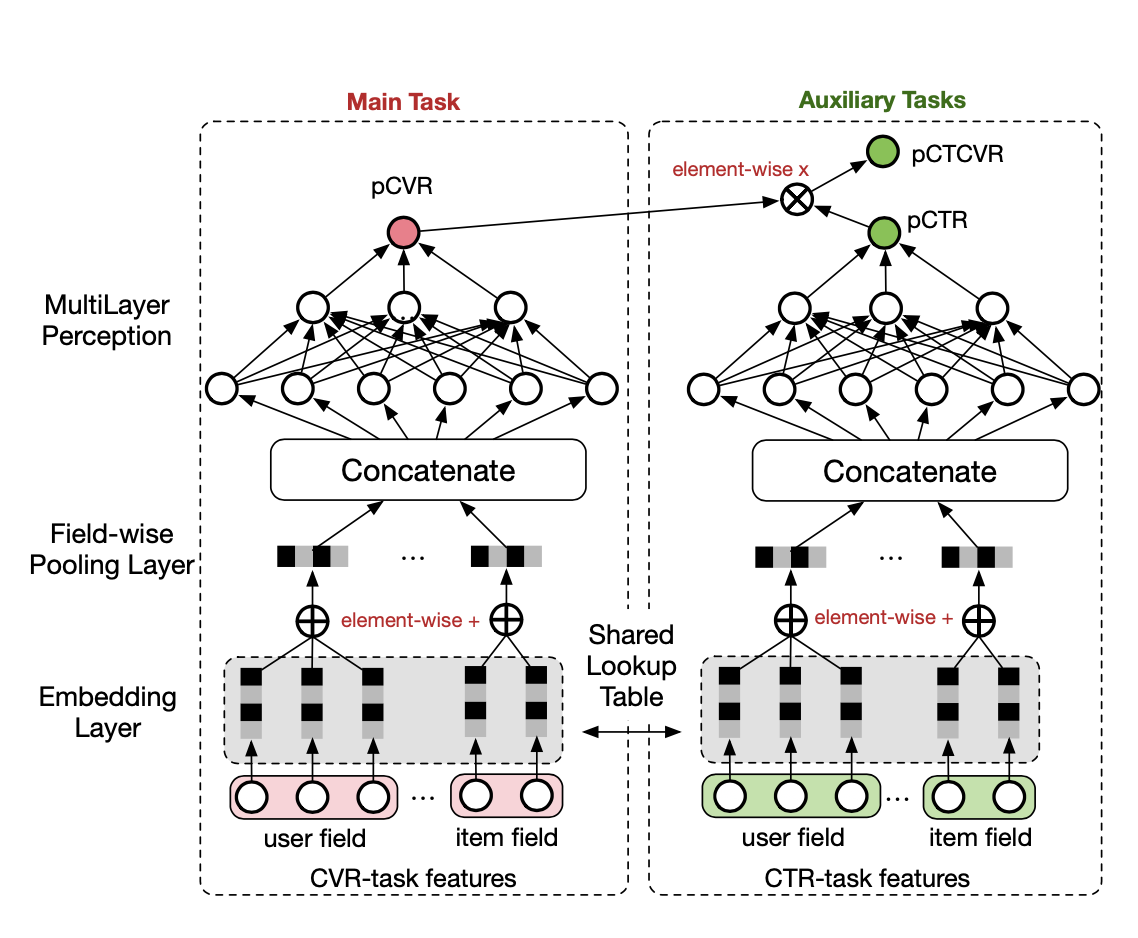
从中能够看到 ESMM 的两个特点：

1. CTR 与 CVR 这两个塔，共享底座 embedding。 因此 CVR 样本数量太少了，也就是存在开头提到的两个问题中的数据稀疏问题，所以很难充分训练学到好的 embedding 表达，但是 CTR 样本很多，这样共享底座 embedding，有点 transfer learning 的味道，帮助 CVR 的 embedding 向量训练的更充分，更准确。
2. CVR 这个塔其实个中间变量，他没有自己的损失函数也就意味着在训练期间没有明确的监督信号，在 ESMM 训练期间，主要训练的是 CTR 和 CTCVR 这两个任务，这一点从 ESMM 的 loss 函数设计也能看出来。

ESMM 的损失函数如下：

\[L(\theta_{cvr}, \theta_{ctr}) = \underset{CTR}{\underbrace{\sum_{i=1}^N l(y_i, f(x_i; \theta_{ctr}))}} + \underset{CTCVR}{\underbrace{\sum_{i=1}^N l(y_i\&z_i, f(x_i; \theta_{ctr} \times f(x_i; \theta_{cvr}))}} \tag{2} \]

用交叉熵的形式把上面的损失函数细致的描述下：

\[\begin{aligned} L(\theta_{cvr}, \theta_{ctr}) &= \underset{CTR}{\underbrace{\sum_{i=1}^N l(y_i, f(x_i; \theta_{ctr}))}} + \underset{CTCVR}{\underbrace{\sum_{i=1}^N l(y_i\&z_i, f(x_i; \theta_{ctr} \times f(x_i; \theta_{cvr}))}} \\ &= -\frac{1}{N}\sum_{i=1}^{N}(y_ilog\hat{y_i} + (1-y_i)log(1-\hat{y_i})) + -\frac{1}{N}\sum_{i=1}^{N}(y_i\& z_ilog(\hat{y_i}\times\hat{z_i}) + (1-y_i\& z_i)log(1-\hat{y_i}\times\hat{z_i})) \end{aligned} \]

我们在实现的时候，上面 \(y i \& z i\) ，实际上就是转化的 label，因为有转化的必然有点击。

DCN

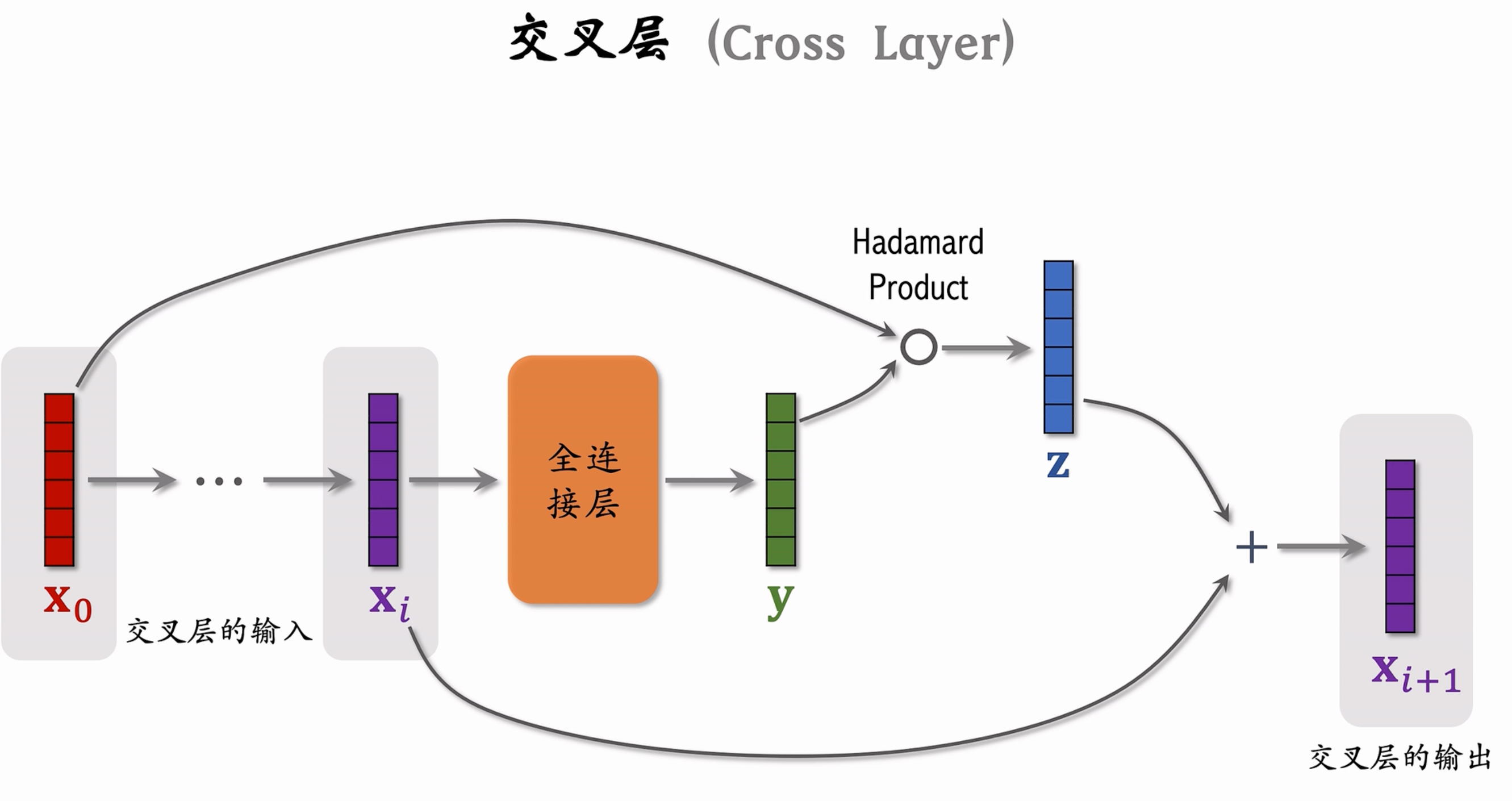
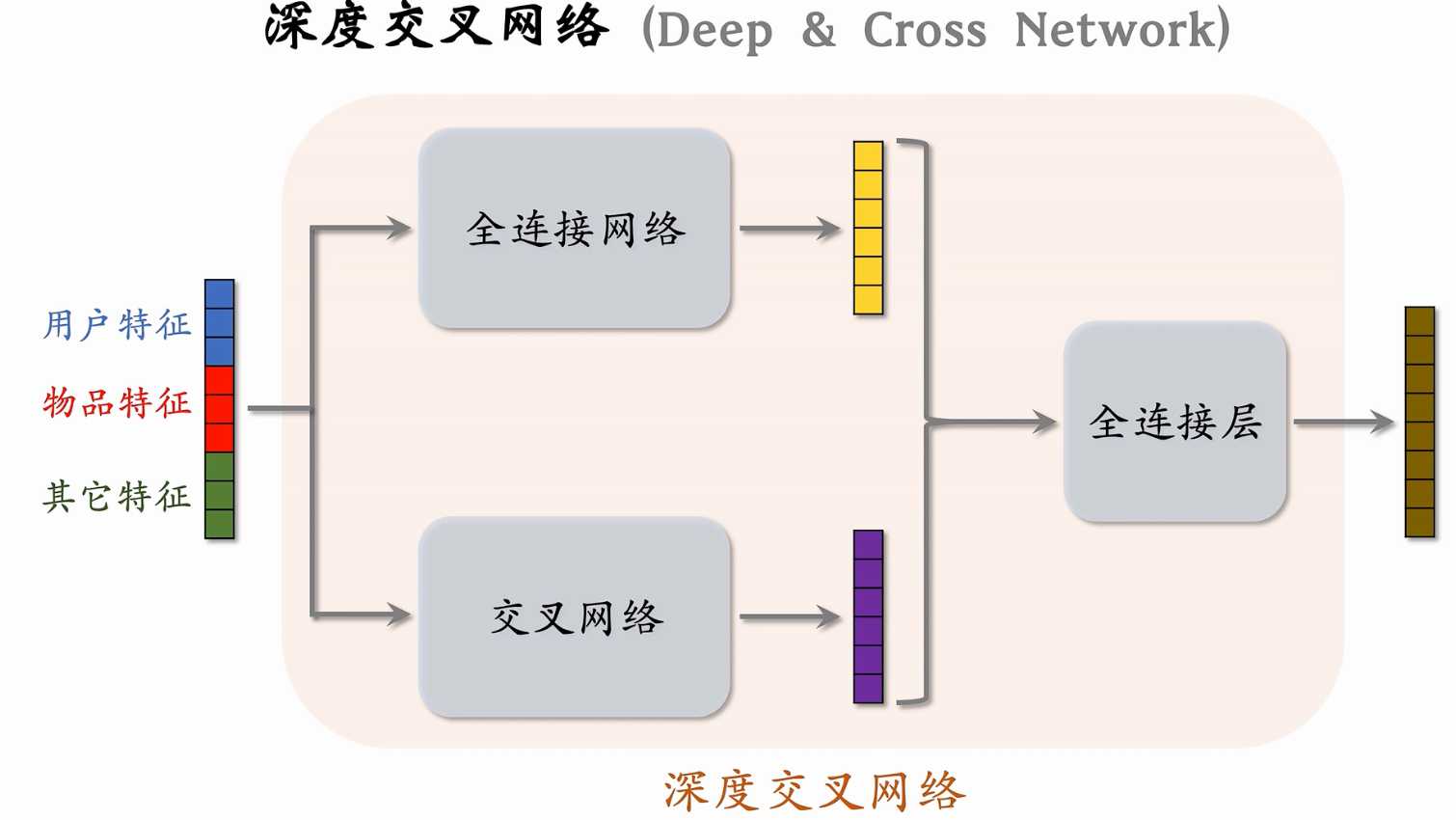
DCN的特点

1. 使用cross network，在每一层都应用feature crossing。高效的学习了bounded degree组合特征。不需要人工特征工程。
2. 网络结构简单且高效。多项式复杂度由layer depth决定。
3. 相比于DNN，DCN的logloss更低，而且参数的数量将近少了一个数量级。

Cross 层特征交叉的推导过程

DCN 全称 Deep Crossing Network，模型介绍可以见 这篇文章。DCN 的关键设计在于 Cross 层，假设输入为特征向量 \(x_0\)​，其每一层的运算过程为 :

\[x_{i+1}=x_0x_{i}^Tw_{i+1}+x_i \]

可视化为：

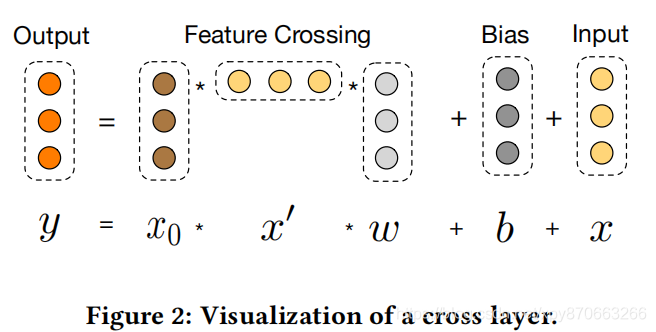
前面推荐阅读的文章详细推导了为什么有 \(i\) 层的 Cross 操作可以得到从 1 阶到 \(i+1\) 阶的任意的特征组合，这里截图放在这里方便后面引用其中符号：

来自 xDeepFM 的 diss

后来看到 xDeepFM 的论文，其首先证明了 Cross 操作的输出是输入 \(x_0\) ​ 的标量倍，证明过程：

该论文的总结我是比较认同的，即 DCN 的缺点在于两点，一是其输出仍然是输入的标量倍，二是这种特征交互是将特征向量的每一位（bit）看做是一个特征，才可以认为是得到了高阶的交叉特征（特征的连乘）。但是对于这两点我认为需要补充一些想法：

关于第一点，即 DCN 的输出仍然是输入的标量倍。从这个结论并不是很直观能看到 Cross 运算的缺陷，从前面的推导过程来看，最后输出的特征向量确实包含了从 1 阶到 \(i+1\) 阶交叉特征（一阶的 \(x_0\) 、 \(x_1\) ，二阶的 \(x_0^2\) 、 \(x_0x_1\) 等等），交叉特征都在每个分量内部作为求和项了，也都含有参数项。但一个容易被忽略的事实是：交叉特征的系数并非相互独立。举个例子，在得到的 \(X_1\) 向量表达式中：

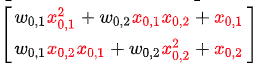
假设将两个分量直接相加（加权相加结论也不变），二次项 \(x_{0,1}x_{0,2}\) 的系数 \(w_{0,1}+w_{0,2}\) 正是 \(x_{0,1}^2\) 的系数 \(w_{0,1}\) 与 \(x_{0,2}^2\) 的系数 \(w_{0,2}\) 的线性组合。如果用最传统的方法（Wide&Deep 的 Wide 一侧仍然是这种思路），直接手工构造交叉特征并使用逻辑斯谛回归来拟合的话，每个交叉特征应该有独立于其他特征的参数，而此处 DCN 虽然得到所有交叉特征，但系数却是相互限制的，自由度低了很多，因此并不能等价于传统的手动构造交叉特征 + LR，这自然会限制其表达能力。

关于第二点，即特征交互是一种 bit-wise 的方式，这种隐式的 “特征交叉” 使用 DNN 即可完成（Despite the powerful ability of learning an arbitrary function from data, plain DNNs generate feature interactions implicitly and at the bit-wise level.）。确实，如果输入的特征向量是 Embedding 层的输出，Cross 操作就是在特征的 bit 上做交叉，并没有直观上的含义。不过，如果我们给定的输入是原始特征：对于数值型特征直接使用其值，对于类别型特征，将其转换成 \(k\) 个二元特征， \(k\) 为原本的类别数目，那么 Cross 操作得到的交互就是特征级别的了。

参考资料：

• https://www.bilibili.com/video/BV1LP411L7Z2/?spm_id_from=333.788&vd_source=a70439aae0ce70e41b5fe1a6dc35d6c8
• https://github.com/duboya/CTR-Prediction/blob/master/Deep %26 Cross Network 学习笔记.pdf

LHUC（PPNet）

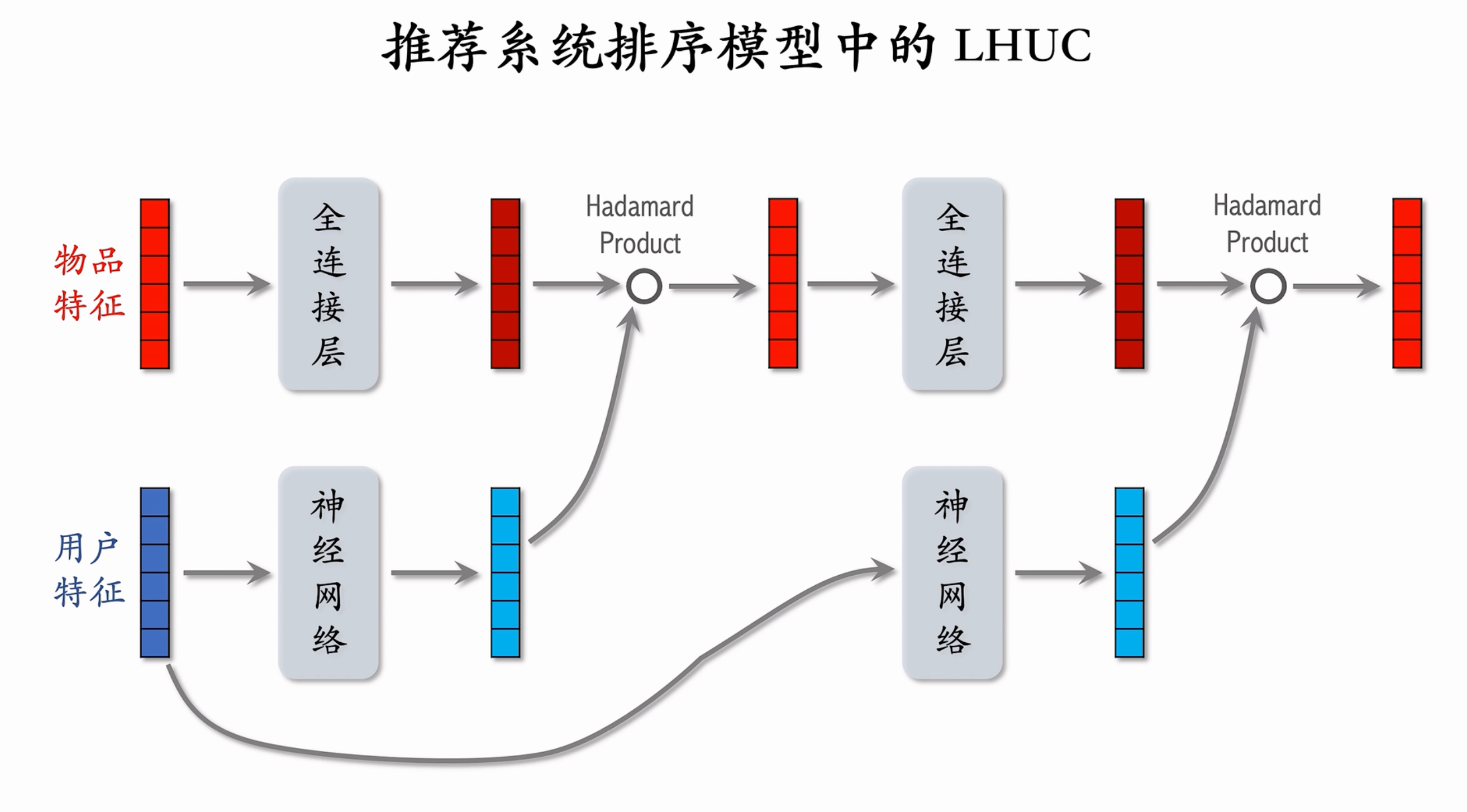
SENET

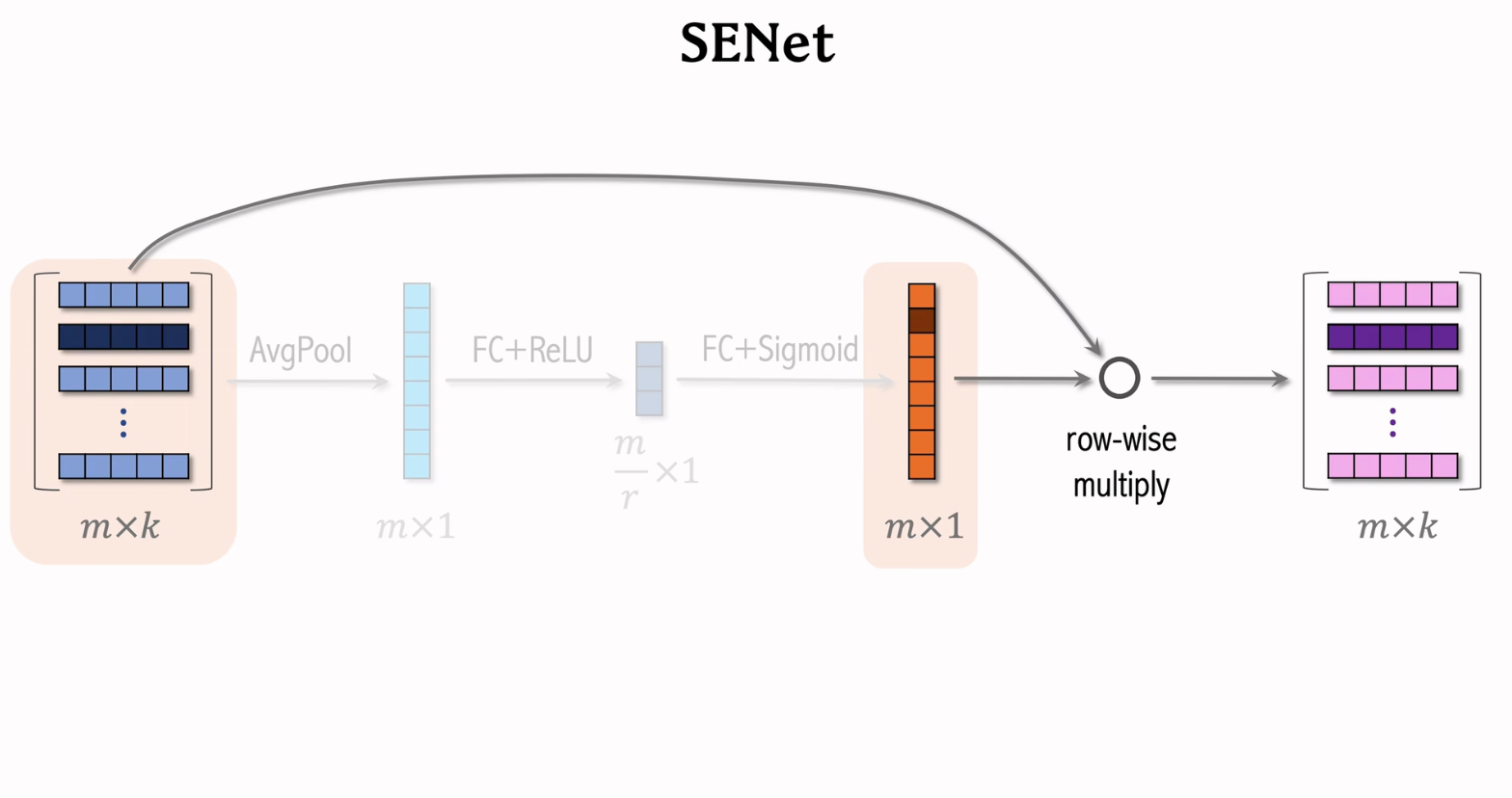
DIN

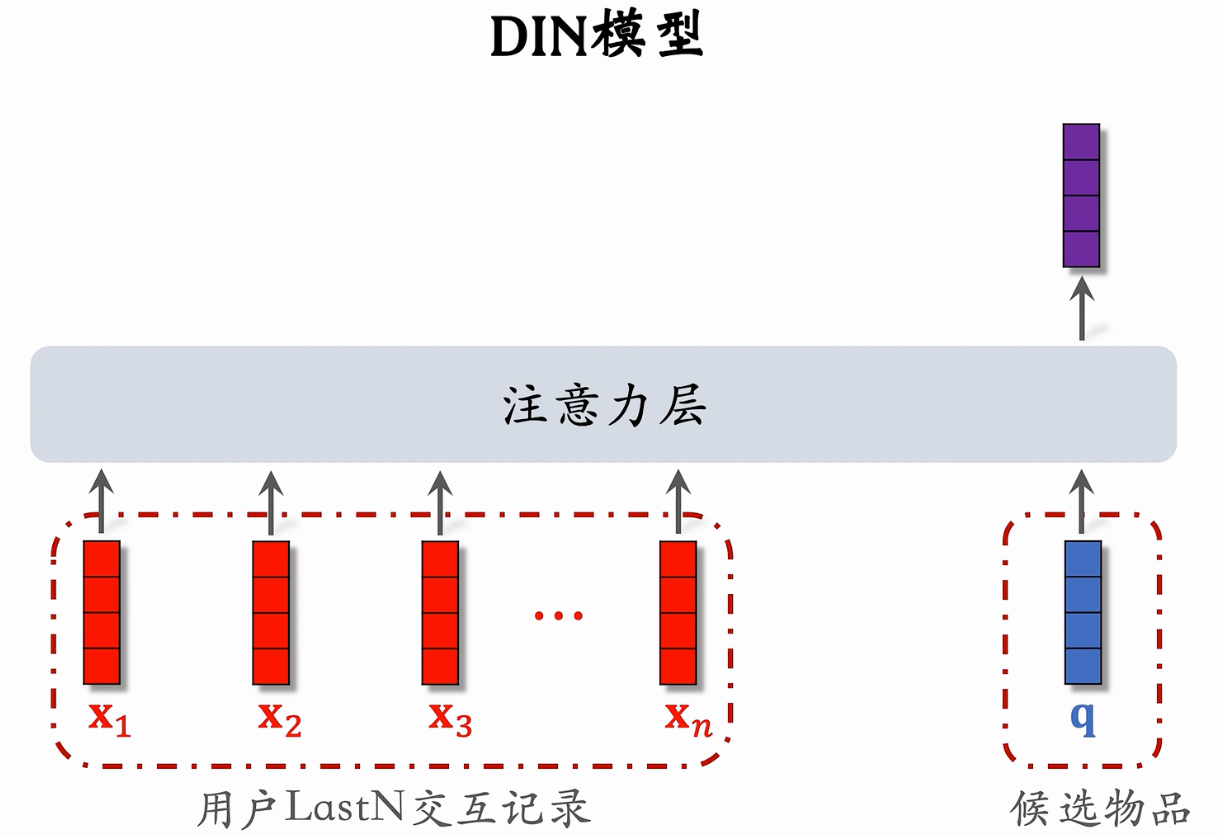
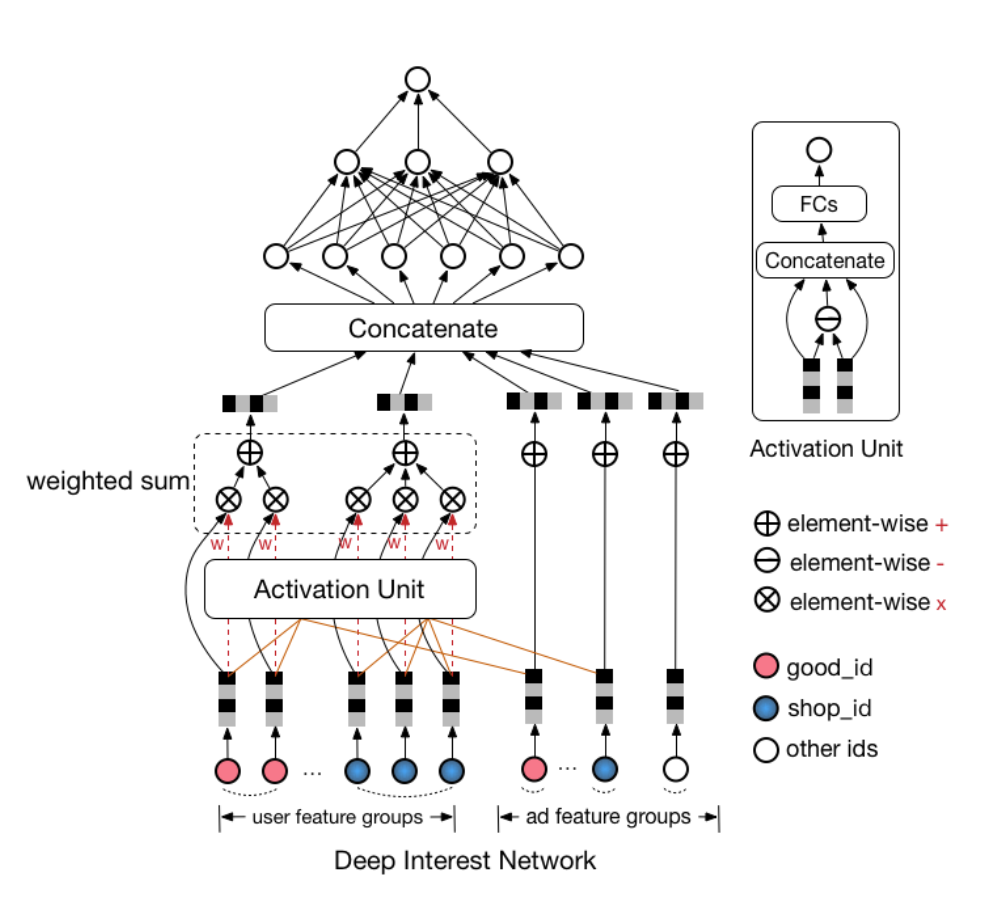
假设 \(V_i^{shop},V_i^{good},V_i^{cate}\) 分别表示历史第 \(i\) 次点击的 shop_id，good_id，cate_id， \(V_a^{shop},V_a^{good},V_a^{cate}\) 分别表示候选商品的 shop_id，good_id，cate_id，则两个不同版本用户兴趣表达 \(V_u\) 计算方式如下

\[\begin{align} g\left( V_i^{shop},V_a^{shop} \right)&=FC\left( Concat\left( \left[ V_i^{shop},V_a^{shop},V_i^{shop}-V_a^{shop},V_i^{shop}\ast V_a^{shop} \right] \right) \right) \\ g\left( V_i^{good},V_a^{good} \right)&=FC\left( Concat\left( \left[ V_i^{good},V_a^{good}, V_i^{good}-V_a^{good}, V_i^{good}\ast V_a^{good} \right] \right) \right) \\ V_u^{shop}&=\sum_{i=1}^{N}{g\left( V_i^{shop},V_a^{shop} \right)V_i^{shop}} \\ V_u^{good}&=\sum_{i=1}^{N}{g\left( V_i^{good},V_a^{good} \right)V_i^{good}} \\ V_u&=Concat\left( \left[ V_u^{shop},V_u^{good} \right] \right) \end{align} \tag{2} \]

DIN的缺点

• 缺点
  • 用户兴趣应该是不断进化的。DIN抽取的用户兴趣是固定的，没有捕获到兴趣的这种进化性
  • 注意力层的计算量正比于n（用户行为序列的长度）
  • 只能记录最近几百个物品，否则计算量太大。
  • 关注短期兴趣，遗忘长期兴趣

参考资料：

• https://blog.csdn.net/u012328159/article/details/123043033
• https://zhuanlan.zhihu.com/p/103092757?utm_medium=social&utm_psn=1811383167061475328&utm_source=wechat_session
• https://www.bilibili.com/video/BV1Ze4y1B7JL/?p=28&spm_id_from=pageDriver

SIM

SIM模型

• 保留用户长期行为记录，n 的大小可以是几千。

• 对于每个候选物品，在用户LastN 记录中做快速查找，找到k个相似物品。

• 把LastN 变成 TopK，然后输入到注意力层。

• SIM 模型减小计算量(从n降到k)。

第一步：查找

• 方法一:Hard Search
  • 根据候选物品的类目，保留LastN 物品中类目相同的
  • 简单，快速，无需训练。
• 方法二:Soft Search
  • 把物品做 embedding，变成向量
  • 把候选物品向量作为query，做k近邻查找，保留LastIN物品中最接近的k个。效果更好，编程实现更复杂。

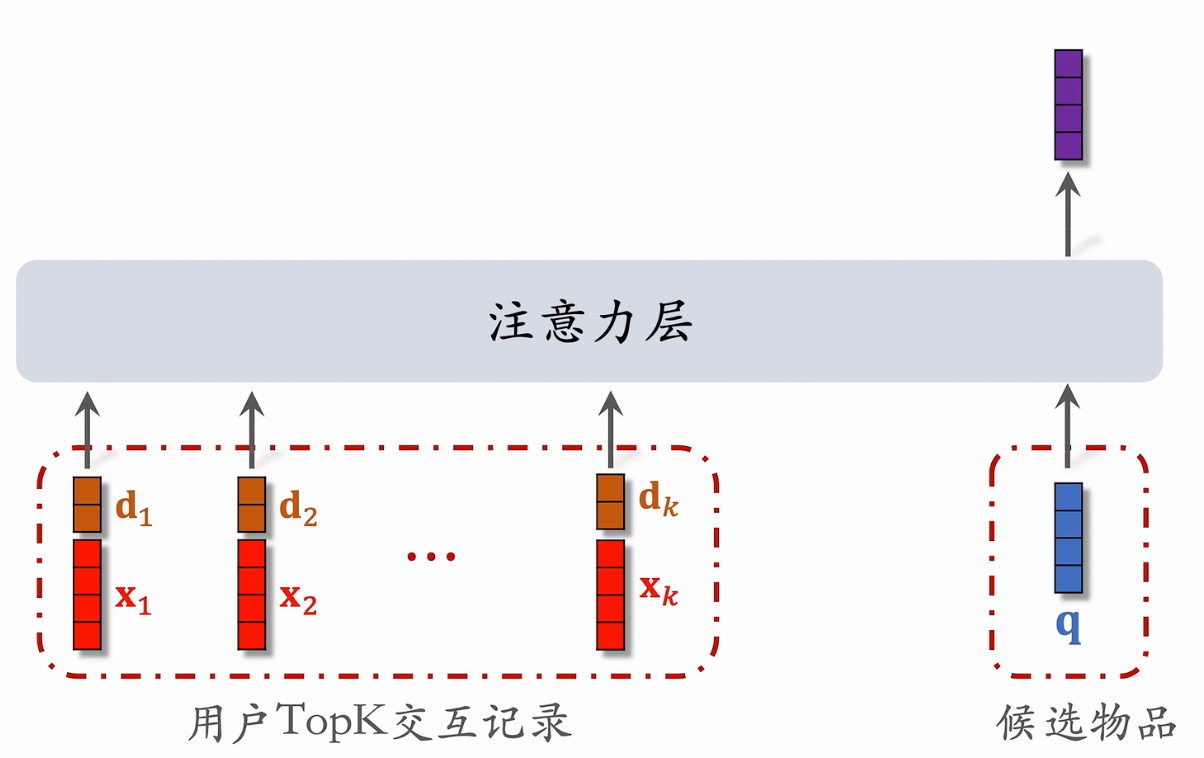
第二步：注意力机制

使用时间信息

• 用户与某个LastN 物品的交互时刻距今为δ。
• 对δ做离散化，再做embedding，变成向量d把两个向量做concatenation，表征一个LastN物品。
• 向量x是物品 embedding。向量d是时间的 embedding 。

参考资料：

• https://www.bilibili.com/video/BV1Ze4y1B7JL/?p=28&spm_id_from=pageDriver

GAUC

DIN在模型的评估上，定义了 GAUC:

\[GAUC=\frac{\sum_{i=1}^{n}{\text{impression}_i\times AUC_i}}{\sum_{i=1}^{n}\text{impression}_i}\tag4 \]

其中 \(n\)表示用户数， \(\text{impression}_i\) 和 \(AUC_i\)分别表示第 \(i\) 个用户的曝光和 AUC，新的 AUC 更贴近线上真实情况，因为最终我们是按每个用户进行排序的。

GAUC的缺点：

• GAUC是单用户的sample求auc以后再平均，但是单用户行为没有那么多的时候，会抖动

参考资料：https://blog.csdn.net/qfikh/article/details/105390002

AUC

• ROC曲线：ROC曲线的横坐标是FPR（表示实际为负的样本有多少预测成了正），纵坐标是TPR（表示实际为正的样本有多少预测成了正）。对于一个分类器的输出通常是概率阈值。通过改变阈值大小，会输出不同的FPR和TPR的值，将其连接起来则得到ROC曲线

AUC 的计算公式

\[AUC = \frac{\sum_{a\in P}^{}{rank_i}-\frac{|P|*(|P|+1)}{2}}{|P|*|N|} \]

接下来，我们解释一下这个公式：

P：表示正样本

N：表示负样本

|P|：表示正样本数量

|N|：表示负样本数量

| \(rank_{i}\) |：表示根据模型的预测分数排行，i 号样本的顺序编号。

好的，我们来看一下，这个公式是怎么推演出来的？

编号	样本	模型预测值
1	p1	0.25
2	p2	0.3
3	n1	0.4
4	p4	0.80
5	n2	0.80
6	n3	0.80
7	p5	0.85
8	n4	0.89
9	n5	0.95
10	p3	0.96

假如我们现在存在 10 个样本，并且模型对 10 个正样本都给出了对应的预测值，最后我们还按照模型的预测值的大小进行了排序。那么 \(rank_{i}\)rank_{i} 即表示样本排序后的编号。

好，我们说：

AUC 等于随机挑选一个正样本和负样本时，模型对正样本的预测分数大于负样本的预测分数的概率。

对于预测概率第 1 大的正样本，也就是编号为 10 的样本，在上表中对应 P1，那么比他小的负样本的个数为 \(rank_{n} - (\left| P \right|)\)。

对于预测概率第 2 大的正样本，也就是编号为 7 的样本，在上表中对应 P5，那么比他小的负样本的个数为 \(rank_{n-1} - (\left| P \right| - 1)\)。

找规律一直下去：

对于预测概率最小的正样本，比他小的负样本的个数为 \(rank_{1} - 1\) 。

好的，那么这样其实分子就出来了，我们把他们加和处理。

\[rank_{n} - (\left| P \right|) + rank_{n-1} - (\left| P \right| - 1) + \cdots + rank_{1} - 1 = \sum_{a\in P}^{}{rank_i}-\frac{|P|*(|P|+1)}{2} \]

那我们只需要求解分母就可以了，任意去一个正样本和一个负样本，共有 \(|P|\times|N|\) 种方案。

那么现在这个公式是不是就表示，挑选一个正样本和负样本，正样本的预测分数大于负样本的预测分数的概率了呢？

\(AUC = \frac{\sum_{a\in P}^{}{rank_i}-\frac{|P|*(|P|+1)}{2}}{|P|*|N|}\)

那么，我们计算一下改表格对应的 AUC 是多少？

编号	样本	预测分数
1	p1	0.25
2	p2	0.3
3	n1	0.4
4 --> 5	p4	0.80
5 --> 5	n2	0.80
6 --> 5	n3	0.80
7	p5	0.85
8	n4	0.89
9	n5	0.95
10	p3	0.96

可以看到，这里面包含了一些预测分数相等的行，对于这样的数据，我们只需要对编号进行加和重新平均即可。将编号4、 5、6 替换成 5。

好的，代公式：

\[AUC = \frac{\sum_{a\in P}^{}{rank_i}-\frac{|P|*(|P|+1)}{2}}{|P|*|N|} = \frac{(1+2+5+7+10) - \frac{5*(5+1)}{2}}{5*5} = 0.4 \]

参考资料：https://zhuanlan.zhihu.com/p/361214293

AUC 含义的理解

---

注：下面的说明不是严格的证明，只是帮助通俗理解。

那么，应该怎么将 AUC 的值与概率联系起来呢？首先，我们知道整个区域的面积是 1。假设正样本的数量为 \(M\) ，负样本数量为 \(N\)，并且在改变阈值的过程中，每当一个样本从被预测为正，变为被预测为负，则：

• 若此样本为正样本，则 TPR 将减小 \(\frac{1}{M}\)
• 若此样本为负样本，则 FPR 将减小 \(\frac{1}{N}\)

由于每让一个样本的预测结果发生变化，都画出了一条线段，因此让每个样本对应一条线段，负样本对应上方水平的线段，正样本对应右侧垂直的线段。于是可以将整个区域划分为 \(M\times N\) 个小区域，每个区域可以由一条垂直的线段和一条水平的线段通过平移组成，那么这个区域就可以代表这两条线段对应的一个正样本和一个负样本组成的样本对，如下图。

那么我们来理解一下图中黄色区域代表什么？这个黄色部分代表的其实是所有得分比 n2 的得分高的正样本与 n2 组成的样本对。也就是说黄色的部分由 4 个小块组成，每个小块是一个样本对，在这个样本对中，正样本的得分比负样本得分高。

所以，我们可以得到结论，ROC 曲线下面的所有小块代表的样本对都是正样本得分比负样本得分高的样本对。而我们也可以证明 ROC 上面的所有小块代表的样本对都是正样本得分比负样本得分低的样本对。

现在，你能否理解 AUC 的含义了呢：随机给定一个正样本和一个负样本，用一个分类器进行分类和预测，该正样本的得分比该负样本的得分要大的概率。

而根据这一含义，我们也可以确定，AUC 越大（越接近 1），模型的分类效果越好。

参考资料：https://www.zhihu.com/question/39840928/answer/1085753375

线下AUC提升为什么不能带来线上效果提升?

1. 样本
   • 线下评测基于历史出现样本，而线上测试存在新样本。因此线下AUC提升可能只是在历史出现样本上有提升，但是对于线上新样本可能并没有效果。
   • 数据本身由老模型产生，本身也是存在偏置的。
   • 和线下特征不一致。例如包含时间相关特征，存在特征穿越。或者线上部分特征缺失等等。
2. 评估目标
   • AUC计算的时候，不仅会涉及同一个用户的不同item，也会涉及不同用户的不同item，而线上排序系统每次排序只针对同一个用户的不同item进行打分。
   • 线上效果只和用户看到后的点击的可能性有关，和position等偏置因素无关的。而线下一般是不同position的样本混合训练，因此线上和线下评估不对等。
3. 分布变化：DNN模型相比传统模型，一般得分分布会更平滑，和传统模型相比打分布不一致。而线上有些出价策略依赖了打分分布，例如有一些相关阈值，那么就可能产生影响。这个可以绘制CTR概率分布图来检查。

参考资料：https://zhuanlan.zhihu.com/p/58152702

特征穿越

对于使用过去以及当下信息来预测未来的AI算法模型，特征穿越本质上是，特征中包含了未来的信息。

对于线上推理过程，构建特征所使用的信息只能来自当下或过去，自然不存在特征穿越问题。

而对于线下训练过程，构建特征时可能会误引入样本发生时刻之后的信息，导致特征穿越。

当训练过程中存在特征穿越问题时，训练评估结果极佳，但线上效果往往会迥然不同。因为模型在训练评估时，使用了特征中的未来信息，而在线上推理时，特征中不再包含未来信息，导致了显著的Training-Serving Skew。

参考资料：https://zhuanlan.zhihu.com/p/402812843

评价指标

假设对于一个查询，真实相关的结果是 {A，C，E, Q}，模型得到 5 个结果 {A, B, C, D, E}，则其中只有 A，C，E 是相关的，标记为 {1, 0, 1, 0, 1}，1 表示相关，0 表示不相关。

recall@k

预测正确的相关结果占所有相关结果的比例：

\[\text{Recall@k} = \frac{\text{TP@k}}{\text{TP@k}+\text{FN@k}} \]

取值范围 [0,1]，越大越好。

例子：

Recall@3 = 2/4 = 0.50

Recall@4 = 2/4 = 0.50

Recall@5 = 3/4 = 0.75

precision@k

即预测正确的相关结果占返回的所有结果的比例：

\[ Precision@k = \frac{TP@k}{TP@k+FP@k} \]

取值范围 [0,1]，越大越好。

例子：

Precision@3 = 2/3 = 0.67

Precision@4 = 2/4 = 0.50

Precision@5 = 3/5 = 0.60

F1@k

即 Precision@k 和 Recall@k 的调和平均数：

\[F1@k = \frac{2 \times Precision@k \times Recall@k}{Precision@k+Recall@k} \]

取值范围 [0,1]，越大越好。

例子：

F1@3 = (2 * 0.67 * 0.50)/(0.67 + 0.50) = 0.57

F1@4 = (2 * 0.50 * 0.50)/(0.50 + 0.50) = 0.50

F1@5 = (2 * 0.60 * 0.75)/(0.60 + 0.75) = 0.67

注意：Precision@k、Recall@k、F1@k 评价指标都是与返回顺序无关的。

参考资料：https://blog.csdn.net/guolindonggld/article/details/121114309

map

在了解 MAP(Mean Average Precision) 之前，先来看一下 AP(Average Precision), 即为平均准确率。

对于AP可以用这种方式理解: 假使当我们使用google搜索某个关键词，返回了10个结果。当然最好的情况是这10个结果都是我们想要的相关信息。但是假如只有部分是相关的，比如5个，那么这5个结果如果被显示的比较靠前也是一个相对不错的结果。但是如果这个5个相关信息从第6个返回结果才开始出现，那么这种情况便是比较差的。这便是AP所反映的指标，与recall的概念有些类似，不过是“顺序敏感的recall”。

比如对于用户 u, 我们给他推荐一些物品，那么 u 的平均准确率定义为：

\[\frac{1}{|\Omega_u|} \sum_{i \in \Omega_u} \frac{ \sum_{i \in \Omega_u} h(p_{uj} < p_{ui}) + 1}{p_{ui}} \]

其中，\(\Omega_u\) 表示 ground-truth 的结果，\(p_{ui}\) 表示物品 i 在推荐列表中的位置，\(p_{uj} < p_{ui}\) 表示 j 物品在推荐列表中排在 i 物品之前。

用一个例子来解释AP的计算过程：

推荐列表中的排序	是否在 ground-truth 中	该位置的 Precision
1	1	1/1 = 1
2	0	0
3	1	(1+1)/3 = 0.66
4	0	0
5	0	0
6	1	(2+1) / 6 = 0.5

因此该 user 的 AP 为 (1 + 0.66 + 0.5) / 3 = 0.72

那么对于 MAP(Mean Average Precision)，就很容易知道即为所有用户 u 的 AP 再取均值 (mean) 而已。那么计算公式如下：

\[MAP = \frac{\sum_{u \in \mathcal{U}^{te}}{AP_u}}{\mathcal{U}^{te}} \]

hitrate

在top-K推荐中，HR是一种常用的衡量召回率的指标，其计算公式如下：

\[HR@K = \frac{Number \ of \ Hits @ K}{|GT|} \]

分母是所有的测试集合，分子是每个用户top-K推荐列表中属于测试集合的个数的总和。举个简单的例子，三个用户在测试集中的商品别是10，12，8，模型得到的top-10推荐列表中，分别有6个，5个，4个在测试集中，那么此时HR的值是 (6+5+4)/(10+12+8) = 0.5。

理解：hitrate 表示推荐列表中用户实际感兴趣（例如实际点击或购买）的项目所占的比例。

参考资料：

• https://github.com/duboya/CTR-Prediction/blob/master/Recommendation System/推荐系统中的常用评测指标.md
• https://blog.csdn.net/m0_68682144/article/details/135675207

PCOC（Predict Click Over Click）

参考资料：https://www.woshipm.com/pd/5843246.html

\[PCOC = Pctr / Actr \]

PCOC指标越接近于1，意味着CTR预估的越准确。PCOC > 1，则代表CTR被高估；PCOC < 1，则代表CTR被低估。但PCOC指标是统计所有PV的Pctr和Actr效果，这里面可能会存在一定的统计偏差。假设样本里有50%PV的CTR被高估了，50%PV的CTR被低估了，最终二者汇总在一起时PCOC可能还是趋近于1。

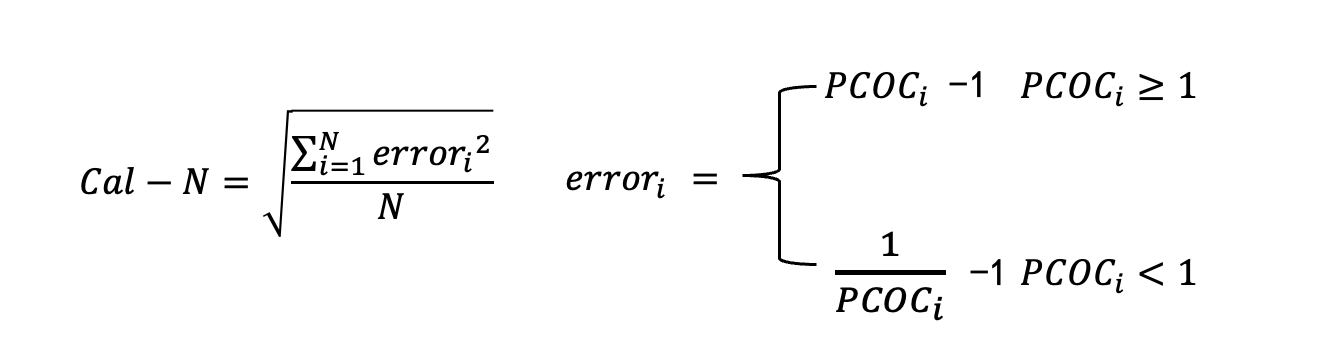
Calibration-N

为了解决上述PCOC指标可能存在的统计偏差，我们使用一个新的指标Cal-N。首先将统计样本分为几个簇，然后按照簇分别去统计PCOC指标，再分别计算各个簇PCOC指标与标准值1之间的偏差，最后进行汇总。这种统计方式就可以避免单独的PCOC指标里可能存在的统计偏差。

copc

参考资料：https://www.cnblogs.com/Lee-yl/p/15061680.html

\[copc = (real\ cvr) / pcvr \]

分析办法：把 rank 分数分成若干区间，每个区间统计真实的 ctr，更*一步，可以拆分成多个桶，比如按照某个特征拆分成 A，B 两组，单独统计每组的真实 ctr

• rank 分数单调递增，ctr 没有单调递增：

  这个原因多半是你线上线下分布不一致导致的，道理很简单，如果你的 rank 真的拟合好了分布，没理由高分数区间段的 ctr 会低于低分数区间。这个不一致，有可能是你特征没做好线上线下的统一，也有可能是你模型没拟合好线上的分布。总之这种情况，你先别急着加特征，先把线上线下特征梳理一下，看看分布是否一致，或者模型训练是不是有问题。

• rank 分数单调递增，ctr 单调递增，但是增长非常慢:

  比如说 0.9-1.0 区间的 ctr 仅仅比 0.3-0.4 区间的 ctr 高一丁点。这个原因才是你模型缺特征，尤其是缺乏活跃用户的特征，通常活跃用户，系统 rank 为了指标，会使用很重的行为画像作为特征，很容易放大历史点击记录，更加倾向于把他们排上去，如果你高估了该用户的点击倾向，就会导致分数给的很高，但是现实用户不怎么点的现象

  这个也会触发新的问题，也就是常说的离线 AUC 很高，但是线上没效果，道理都一样，你模型仅仅是把正负样本的间隔拉开了，并没有真正改善用户看到的内容和布局，才导致高分段 ctr 不见增长。

• rank 分数单调递增，ctr 也单调递增，但是 A，B 两组的 ctr 比值差异过大：

  比如 A，B 表示上午和下午，如果这两个时间段，同一个分数区间的 ctr 差异过大，说明模型对时间这个维度的建模不足，需要进一步改善。

• rank 分数单调递增，ctr 单调递增，各种维度分组下的 ctr 比值也接稳：

  恭喜你，到达这一步，表示你 rank 几乎没事情可做了，你剩下要做就是优化召回，在策略上引导你 rank 往新的产品思路上走，在更加高的层面带动系统往良性地方发展

用户ID

参考资料：

• https://blog.csdn.net/qq_46006468/article/details/126068670
• https://blog.csdn.net/weixin_31866177/article/details/136034812

为什么需要解决长尾效应：

1. 用户不可能多次点击同一个热门商品，用户购买过了商品后再看到这个商品回引起反感。
2. 推荐种类太少，很多用户是感性消费。
3. 每个用户都有自己的癖好，为了提升用户个性化体验。

解决方案

· 解决曝光偏差（曝光偏差是指用户看到的商品是有限的，看不到他喜欢的商品，反而推荐的不喜欢的商品）：

1.Heuristic：加权的矩阵分解以及动态MF，未观测到的交互被赋予较低的权重，但挑战性较强，不易于实现。
2.Sampling：采样，经常采用的采样策略有均匀的负采样,对于流行的负样本过采样，但是这些策略却较难捕捉到真实的负样本。
3.Exposure-based model：开发基于曝光的模型，这样可以知道一个商品被曝光到某个用户的可能性等。

· 解决流行度偏差（流行度偏差是指推荐热门商品的频率比数据集中显示的原始受欢迎程度还要高，因为模型通常会给热门项目的评分高于其理想值，简单地将不受欢迎的商品预测为负值）：

1.正则：合适的正则可以将模型推向平衡的推荐列表。
2. 对抗训练：通过G和D之间的对抗学习，D学习流行项和利基项之间的隐式关联，G学习捕捉更多与用户历史相关的niche商品，从而为用户推荐更多长尾商品。
3. Causal graph：因果图是反事实推理的有力工具。
4. 其它方法：propensity score也可以被用来做popularity的bias。通过降低流行项对模型训练的影响，可以减轻流行偏差。

user-id和item-id是否需要作为特征

深度学习推荐算法中 user-id 和 item-id 是否需要放入模型中作为特征进行训练呢？ - 知乎

回答 1：

• 大厂会将 user id / item id 作为特征加入推荐模型，因为他们的数据足够多，算力足够强。
• 大厂的 APP 的资深用户的行为足够将他们的 user id embedding 训练出来。
• 大厂 APP 的热门物料会曝光十几万、甚至几十万次，这么多日志足够将这些 item id embedding 充分训练出来。
• 如果小厂的推荐模型就不建议使用这些 id 当 embedding 了，数据不够，你加进去也学习不出来。

另外这些特征加入模型的位置也非常重要，否则也会被淹没在其他特征中，泯然众人矣。

回答 2：

user_id 和 item_id 作为强记忆型特征，是否要放入模型中作为特征进行训练是不能一概而论的。至少需要考虑业务场景的特点、如何放到模型中两个因素。

一般情况下在真实的业务场景中，无论是用户行为还是物品受欢迎程度都呈现长尾分布，少数头部的 user 和 item 占据了样本中的绝大多数，他们的 id embedding 能够得到充分的学习；另一方面，大量的尾部 user 和 item 的在样本中出现的频率很低，因而他们的 id embedding 在模型训练结束后也没有经过几次参数更新，基本上比随机初始化的状态好不了多少。默认情况下，推荐算法都是对中长尾的 user 和 item（比如冷启动用户、新加入的物品）不友好的。

user_id 和 item_id 作为特征直接加入到模型中，基于长尾分布的用户行为日志训练的推荐模型会越来越偏好头部物品，在导致 “富者越富” 的同时伤害中长尾物品的曝光机会和用户满意度。

通过分析精排模型的特征重要度，我们发现重要度较高的特征主要集中在少量的 “记忆性” 特征上，而大量的中长尾特征的重要度都很低。“记忆性” 特征指的是没有泛化能力的特征，如用户 ID、物品 ID、用户对物品 ID 在过去一段时间上的行为统计，在这些特征上无法学到能够迁移到其他物品的知识。常规的模型结构会产生特征重要度的长尾分布，最终带来了模型偏好物品的长尾分布。

总的来说长尾分布越严重的场景越不建议直接加入 user_id 和 item_id 作为特征（也不是绝对的，可以加到特殊的模型结构中，参考下文）。当然这里的长尾分布是按照 user 和 item 分开看的，确实存在一些业务场景在 user 这个维度长尾分布很严重，但在 item 这个维度长尾分布并不突出，这种情况下是可以把 item_id 作为特征直接丢给模型学习的。

具体来说：

• 物品池大小适中且基本保持稳定的场景建议加 item_id 特征；
• 物品池频繁汰换的场景不建议加 item_id 特征；
• 新用户占比很高的场景不建议加 user_id 特征；
• 小流量场景不建议加 user_id 特征；
• 其他场景大家根据 user 和 item 的分布情况自己评估；
• 搞不清楚的时候可以考虑加 item_id，不加 user_id。

如何添加 user_id、item_id 特征？添加在模型结构的什么位置也是有讲究的。

• 物品池大小适中且基本保持稳定的场景 item_id 可以和其他特征放在一起训练
• user_id 等强区分性特征可以放在单独的塔中学习 user bias；不和其他常规特征放在一起。
  • user bias 是有些用户天然喜欢给物品打高分，浏览很广泛，有些用户天然很挑剔
• 在长尾分布较严重的场景，user_id、item_id 等强区分性特征 embedding 可以做特征粒度的 dropout 后再与其他特征 embedding 拼接。注意这里说的是 “特征粒度的 dropout”，不是常规的神经元粒度的 dropout，也就是说特征 embedding 整体有一定的概率被丢弃（mask）或保留。
• 也可以考虑使用 @石塔西提到的 “补水塔” 结构。
• 记忆型特征放在一个单独的塔中，泛化性特征放在另外的独立塔中；引入一个基于物品分布的门控机制，让头部的物品主要拟合 “记忆特征”，中长尾物品主要拟合 “泛化特征”。通过加权求和的方式在各个特征上学习到的表征特征，再去拟合最终的业务目标。参考谷歌的 Cross Decoupling Network (CDN) 。

推荐算法 user_id 在 train 和 serving 时应该怎么用？

推荐算法 user_id 在 train 和 serving 时应该怎么用？ - 知乎

第一次做推荐，看了几篇论文发现都会用到 id 类特征，比如在电商推荐领域，可能会用到 user_id 和 item_id，随机初始化该类特征的向量表进行模型训练，那么在线服务时怎么对未出现的 user_id 进行预测呢？

回答 1：

1、比较简单的做法，直接将那些新 userid 的 embedding 全部设置 0，同样对那些出现次数少的 userid 也设置 0，次数少说明该用户训练不够充分，可以直接设置 0。

2、训练的时候对样本中的 userid 随机采样，将他们的 userid 都设置成同一个 id，让其在模型中训练，serving 的时候新用户以及出现次数少的用户的 embedding 就可以用该 id 的 embedding。

回答 2：

对于新 id（新用户或新物料的 id），一般作法是：

• 训练时，随机初始化
• 预测时，以全零向量代替。

多说一句，以上作法不是 new user id 或 new item id 的专利，而是 Parameter Server 的通常作法。比如遇到一个 new tag, parameter server 也是这样处理这个 new tag 在 train & predict 时的 embedding 的。

这样做是出于简单易行，但并非没有缺点。

为了解决这一问题，业界提出使用 meta-learning 的方式学习出 new user/item id 的最优初值。在《互联网大厂推荐算法实战》的 8.2.3 节对 meta-learning 在推荐冷启动中的应用有专门的论述。书中提出将 meta-learning 应用于推荐算法，不能简单照搬，而需要在应用范围、优化目标、生成方式三个方面进行改造。

回答 3：

1. 把这个 user id 丢掉，或者 0 向量填充

2. 训练的时候对所有长尾的 id 共享一个向量作训练，预测出现新的 id 用这个表示

另外，既然是第一次出现的 user id，必然是新用户了，可以对新用户单独做个冷启动模型。