BatchNorm & LayerNorm

BatchNorm & LayerNorm

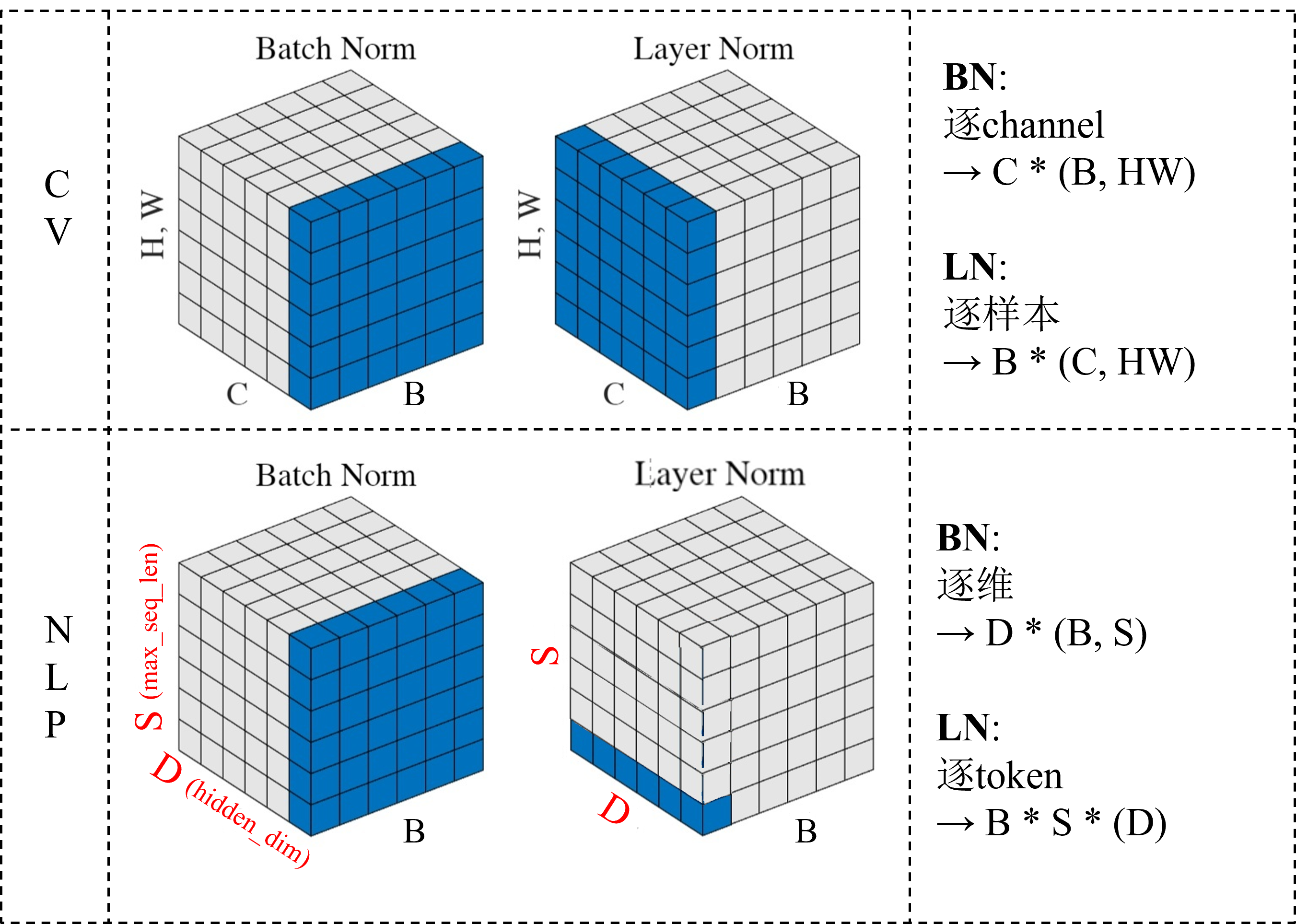
BN和LN

Normalization作用：
1.缓解内部协变量偏移。在深度神经网络中，随着网络层数的加深，每一层的参数更新都可能导致后续层的输入分布发生变化，这种现象被称为内部协变量偏移（Internal Covariate Shift, ICS）。ICS会导致网络训练困难，因为每一层都需要不断适应新的输入分布。LayerNorm通过归一化每一层的输入，减少了层与层之间的输入分布变化，从而有效缓解了ICS问题。
2. 加速收敛速度。 由于输入数据被归一化到较小的范围内，使得激活函数在其饱和区域内的概率减少，从而减少了梯度消失问题，使得网络更容易学习。
3. 增加模型的泛化性能。 Normalization 类似于一种正则化的方式，使得网络对输入数据的小扰动更加鲁棒，从而提高了模型的泛化能力。

BatchNorm

过程

训练阶段：

计算均值和方差：
在训练阶段，对于每个 mini-batch，计算当前 mini-batch 上的均值和方差。
归一化：
使用当前 mini-batch 的均值和方差对特征进行归一化。
更新运行时统计量：
使用指数加权移动平均更新整个训练集的均值和方差，用于在测试阶段进行归一化。
调整缩放和平移参数：
在训练阶段，学习并调整批量归一化层中的缩放和平移参数（gamma 和 beta）。

测试阶段：

使用运行时统计量：
在测试阶段，不再计算当前 mini-batch 的均值和方差，而是使用训练阶段累积的整个训练集的均值和方差。
归一化：
使用训练阶段累积的均值和方差对特征进行归一化。
应用缩放和平移参数：
使用训练阶段学习到的缩放和平移参数对归一化后的特征进行缩放和平移。

BatchNorm 中各变量维度如下：

当输入维度为 \((N, D)\) 时
均值（mean）和方差（variance）：维度为 \((D,)\)，即每个维度上的均值和方差。
归一化后的特征：维度与输入相同 \((N, D)\)。
缩放因子(gamma)和平移因子(beta)：维度也为 \((D,)\)，即每个维度上的缩放和平移参数。
当输入维度为 \((N, H, W, C)\) 时（CV）
均值（mean）和方差（variance）：维度为 \((C,)\)，即每个通道上的均值和方差。
归一化后的特征：维度与输入相同 \((N, H, W, C)\)。
缩放因子(gamma)和平移因子(beta)：维度也为 \((C,)\)，即每个通道上的缩放和平移参数。
当输入维度为 \((N, S, D)\) 时（NLP）
NLP 中的 BN 很模糊，因为一般在 NLP 中不使用 BN，有说输入应该是 \((N, D, S)\) 维度的，按照最上面的图来看：
均值（mean）和方差（variance）：维度为 \((D,)\)，即每个维度上的均值和方差。
归一化后的特征：维度与输入相同 \((N, S, D)\) 或 \((N, D, S)\) 。
缩放因子(gamma)和平移因子(beta)：维度也为 \((D,)\)，即每个维度上的缩放和平移参数。

实现代码(GPT)
由于 NLP 中的 BN 比较模糊，所以没有实现 NLP 中的 BN

import torch

class BatchNorm(torch.nn.Module):
    def __init__(self, num_features, eps=1e-5, momentum=0.1):
        super(BatchNorm, self).__init__()
        self.num_features = num_features
        self.eps = eps
        self.momentum = momentum
        self.gamma = torch.nn.Parameter(torch.ones(num_features))
        self.beta = torch.nn.Parameter(torch.zeros(num_features))
        self.register_buffer('running_mean', torch.zeros(num_features))
        self.register_buffer('running_var', torch.ones(num_features))

    def forward(self, x):
        if self.training:
            mean = x.mean(dim=(0, 2, 3), keepdim=True)
            var = x.var(dim=(0, 2, 3), unbiased=False, keepdim=True)
            self.running_mean = self.momentum * self.running_mean + (1 - self.momentum) * mean.squeeze()
            self.running_var = self.momentum * self.running_var + (1 - self.momentum) * var.squeeze()
        else:
            mean = self.running_mean
            var = self.running_var
        
        x_normalized = (x - mean) / torch.sqrt(var + self.eps)
        out = self.gamma.view(1, -1, 1, 1) * x_normalized + self.beta.view(1, -1, 1, 1)
        return out

LayerNorm

LayerNorm 常在 NLP 中使用，并且在 NLP 中使用的时候更像是 InstanceNorm，相当于是对每个词向量自身(token)做 norm，和 BatchNorm 不同，LayerNorm训练阶段和测试阶段没有区别。

LayerNorm 中各变量维度如下：

当输入维度为 \((N, D)\) 时
均值（mean）和方差（variance）：维度为 \((N,)\)，即每个样本的均值和方差。
归一化后的特征：维度与输入相同 \((N, D)\)。
缩放因子(gamma)和平移因子(beta)：维度也为 \((N,)\)，即每个样本的缩放和平移参数。
当输入维度为 \((N, H, W, C)\) 时（CV）
均值（mean）和方差（variance）：维度为 \((N,)\)，即每个样本的均值和方差。
归一化后的特征：维度与输入相同 \((N, H, W, C)\)。
缩放因子(gamma)和平移因子(beta)：维度也为 \((N,)\)，即每个样本的缩放和平移参数。
当输入维度为 \((N, S, D)\) 时（NLP）
均值（mean）和方差（variance）：维度为 \((N, S,)\)，即每个样本的各个 token 的均值和方差。
归一化后的特征：维度与输入相同 \((N, S, D)\) 。
缩放因子(gamma)和平移因子(beta)：维度也为 \((N, S, )\)，即每个样本的各个 token 的缩放和平移参数。

实现代码

import torch

class LayerNorm(torch.nn.Module):
    def __init__(self, features, eps=1e-5, momentum=0.1):
        super(LayerNorm, self).__init__()
        self.features = features
        self.eps = eps
        self.momentum = momentum
        self.gamma = torch.nn.Parameter(torch.ones(features))
        self.beta = torch.nn.Parameter(torch.zeros(features))
        # self.register_buffer('running_mean', torch.zeros(features))
        # self.register_buffer('running_std', torch.ones(features))

    def forward(self, x):
        mean = x.mean(dim=-1, keepdim=True)
        std = x.std(dim=-1, unbiased=False, keepdim=True)
        # self.running_mean = self.momentum * self.running_mean + (1 - self.momentum) * mean.squeeze()
        # self.running_std = self.momentum * self.running_std + (1 - self.momentum) * std.squeeze()
        x_normalized = (x - mean) / torch.sqrt(std**2 + self.eps)
        out = self.gamma * x_normalized + self.beta
        return out

协变量漂移

参考资料：

协变量漂移

协变量的变化，比如模型应用场景中环境、位置的变化等

注：这里解释下此处的协变量，假设我们要拟合方程 y=wx，对于一个数据对（x，y）:
y为因变量，w为自变量，x为协变量。

一切都要从独立同分布说起。众所周知，在机器学习领域，如果所有样本都由同一个分布产生，且样本之间相互独立，我们就说这些样本独立同分布。如果所有训练样本和测试样本都满足独立同分布，那么，利用训练样本做参数估计得到的分布参数同样适用于测试样本。这样，训练过程才能迅速收敛，模型才能正确预测。

当我们训练一个深度神经网络，实际上就是在用训练样本估计分布参数。然而，神经网络具有层级结构，前一层网络的输出相当于后一层网络的输入。用梯度下降训练模型时，网络参数被不断更新。对于某一层而言，前一层的网络参数一旦发生变化，它的输入分布也会相应改变。这个现象就叫协变量漂移（Covariate Shift）。

谁是协变量？顾名思义，除了第一层网络的输入是自变量以外，其他每层网络的输入都是协变量。由于这些协变量位于网络结构的内部层级，因此这个现象又叫内部协变量漂移（Internal Covariate Shift）。训练时，每个 batch 都会更新一次网络参数。网络层数越深，漂移现象越明显，在 batch 之间不断调整参数以适应不同的协变量分布，导致网络难以收敛。

梯度消失

除了协变量漂移，梯度消失的现象也会影响网络收敛。说到梯度消失，就不得不提到一个概念：饱和非线性函数（Saturating Non-linearity）。众所周知，在神经网络中，我们常用非线性函数作为激活函数。如果一个非线性函数 \(f\)满足如下条件：

\[(\lvert \lim_{x\to -\infty} f(x) \rvert =+\infty)\vee (\lvert \lim_{x\to +\infty} f(x) \rvert =+\infty) \]

我们就称其为不饱和非线性函数。相反，则称其为饱和非线性函数。可以看出，饱和非线性函数总是会把输入压缩到一个较小的范围内。例如，sigmoid 是饱和的，它会把输入输入 \(x\)压缩到 (0, 1) 区间：

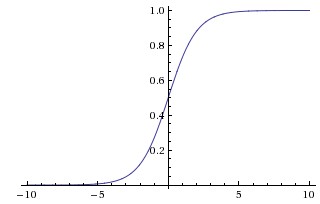
tanh 也是饱和的，它会把输入 \(x\)压缩到 (-1, 1) 区间：

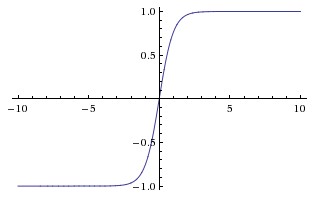
ReLU 是不饱和的，随着输入 \(x\)增加，它也趋于无穷大：

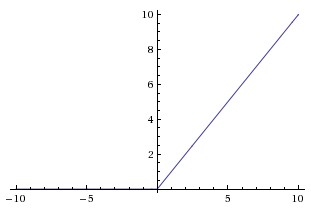
饱和非线性函数有个不好的性质：存在大片导数趋于 0 的饱和区域。反向传播时，如果网络某一层的激活函数的输入正好处于饱和区域，由于计算这一层的权重梯度时需要乘以该层激活函数的导数，因此权重梯度也会变得很小。网络越深，乘法次数越多，梯度就越小，最终导致梯度消失现象，网络收敛速度受到严重影响。

然而，看似简单的算法，背后总是有些问题让人困惑。

归一化得到的 \(\hat{x}_i\)没有直接输出，真正的输出是\(\gamma \hat{x}_i+\beta\)。为什么要这么做呢？

因为每层的输入被归一化之后，会影响这一层本来的表示能力。为了保证每一层仍然具备原有的表示能力，引入两个可学习的变量 \(\gamma\) 和 \(\beta\) 。对于某一层网络，令 \(x^{(k)}\) 表示输入的第 \(k\) 个维度的值，归一化之后，得到 \(\hat{x}^{(k)}\) ：

\[\hat{x}^{(k)}=\frac{x^{(k)}-E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}} \]

当 \(\gamma=\sqrt{Var[x^{(k)}]}, \beta=E[x^{(k)}]\) 时， \(\gamma \hat{x}^{(k)}+\beta\) 可以还原 \(x^{(k)}\) 。

为什么不用整个训练集的数据计算均值和方差？

因为每个 batch 都会更新网络参数，如果你想使用整个训练集的均值和方差，每次参数更新后，都要先把整个训练集输入网络，计算每一层的输出，然后根据每层的输出求出均值和方差，再把下一个 batch 输入网络，用刚才求出的均值和方差做归一化，计算量很大。相反，计算一个 batch 的均值和方差，却可以在这个 batch 的前向传播过程中一并完成。这里的假设是每个 batch 的统计量都是全体训练样本的一个估计。理论上，batch 越大，估计越准。

posted @ 2024-08-27 09:07 Un-Defined 阅读(55) 评论(0) 编辑收藏举报

刷新页面返回顶部

UnDefined

BatchNorm & LayerNorm

BatchNorm & LayerNorm

BatchNorm

过程

LayerNorm

协变量漂移

协变量漂移

梯度消失

公告