特征选择

参考：

https://blog.csdn.net/Datawhale/article/details/120582526

https://zhuanlan.zhihu.com/p/74198735

特征选择

在处理结构型数据时，特征工程中的特征选择是很重要的一个环节，特征选择是选择对模型重要的特征。它的好处在于:

● 减少训练数据大小，加快模型训练速度。

● 减少模型复杂度，避免过拟合。

● 特征数少，有利于解释模型。

● 如果选择对的特征子集，模型准确率可能会提升。

● 去除冗余无用特征，减低模型学习难度，减少数据噪声。

● 去除标注性强的特征，例如某些特征在训练集和测试集分布严重不一致，去除他们有利于避免过拟合。

● 选用不同特征子集去预测不同的目标，比如用不同状态下的作业数特征去预测"提交中的作业数"，而用不同资源使用率的特征去预测“CPU使用率”。

一般流程

特征选择的一般过程：

生成子集：搜索特征子集，为评价函数提供特征子集
评价函数：评价特征子集的好坏
停止准则：与评价函数相关，一般是阈值，评价函数达到一定标准后就可停止搜索
验证过程：在验证数据集上验证选出来的特征子集的有效性

但是，当特征数量很大的时候，这个搜索空间会很大，如何找最优特征还是需要一些经验结论。

三大类方法

根据特征选择的形式，可分为三大类：

Filter(过滤法)：选择特征时不管模型，该方法基于特征的通用表现去选择。比如按照发散性或相关性对各个特征进行评分，设定阈值或者待选择特征的个数进行筛选
Wrapper(包装法)：根据目标函数（往往是预测效果评分），每次选择若干特征，或者排除若干特征
Embedded(嵌入法)：先使用某些机器学习的模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征（类似于Filter，只不过系数是通过训练得来的）

过滤法

● 优点: 特征选择计算开销小，且能有效避免过拟合。

● 缺点: 没考虑针对后续要使用的学习器去选择特征子集，减弱学习器拟合能力。

基本想法是：分别对每个特征 \(x_i\) ，计算 \(x_i\) 相对于类别标签 \(y\) 的信息量 \(S(i)\) ，得到 \(n\) 个结果。然后将 \(n\) 个 \(S(i)\) 按照从大到小排序，输出前 \(k\) 个特征。显然，这样复杂度大大降低。那么关键的问题就是使用什么样的方法来度量 \(S(i)\) ，我们的目标是选取与 \(y\) 关联最密切的一些特征 \(x_i\) 。

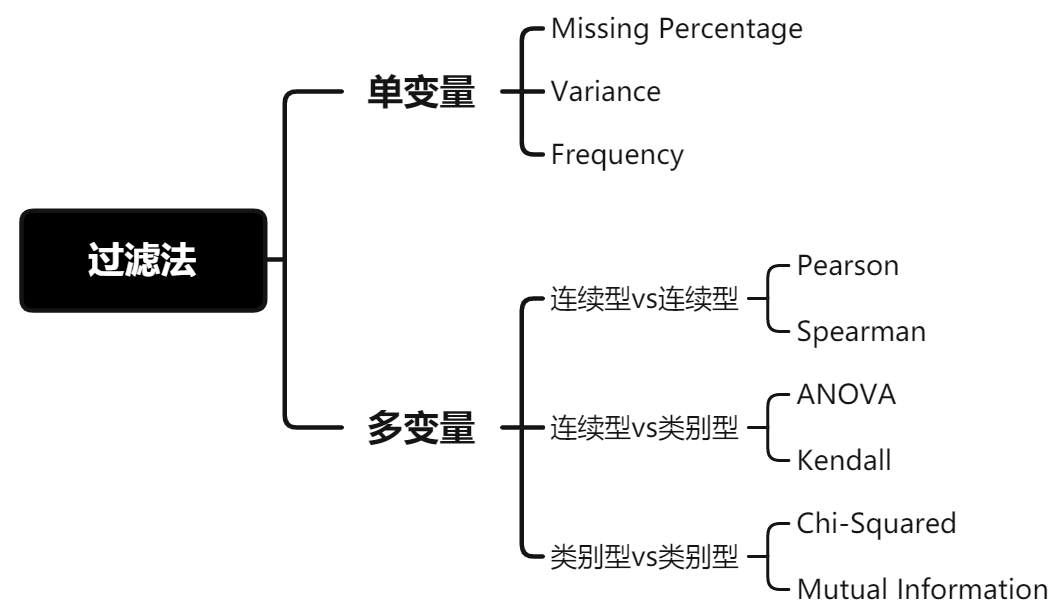
1. 单变量

(1) 缺失百分比(Missing Percentage)

缺失样本比例过多且难以填补的特征，建议剔除该变量。

(2) 方差(Variance)

若某连续型变量的方差接近于0，说明其特征值趋向于单一值的状态，对模型帮助不大，建议剔除该变量。

(3) 频数(Frequency)

若某类别型变量的枚举值样本量占比分布，集中在单一某枚举值上，建议剔除该变量。

# load Boston dataset
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
boston = load_boston()
df = pd.DataFrame(boston.data, columns = boston.feature_names)
 
 
# Missing Percentage + Variance
stat_df = pd.DataFrame({'# of miss':df.isnull().sum(),
                        '% of miss':df.isnull().sum() / len(df) * 100,
                        'var':df.var()})
 
 
# Frequency
cat_name = 'CHAS'
chas = df[cat_name].value_counts().sort_index()
cat_df = pd.DataFrame({'enumerate_val':list(chas.index), 'frequency':list(chas.values)})
sns.barplot(x = "enumerate_val", y = "frequency",data = cat_df, palette="Set3")
for x, y in zip(range(len(cat_df)), cat_df.frequency):
    plt.text(x, y, '%d'%y, ha='center', va='bottom', color='grey')
plt.title(cat_name)
plt.show()

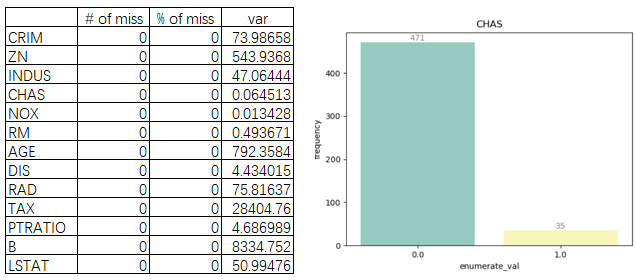
图3: 单变量分析(缺失值、方差和频次图)

由图3发现，NOX方差低和CHAS频次分布严重不平衡，可以考虑剔除。

2. 多变量

研究多变量之间的关系时，主要从两种关系出发:

● 自变量与自变量之间的相关性: 相关性越高，会引发多重共线性问题，进而导致模型稳定性变差，样本微小扰动都会带来大的参数变化[5]，建议在具有共线性的特征中选择一个即可，其余剔除。

● 自变量和因变量之间的相关性: 相关性越高，说明特征对模型预测目标更重要，建议保留。

由于变量分连续型变量和类别型变量，所以在研究变量间关系时，也要选用不同的方法:

2.1 连续型vs连续型

(1) Pearson相关系数

Pearson相关系数是两个变量的协方差除以两变量的标准差乘积。协方差能反映两个随机变量的相关程度（协方差大于0的时候表示两者正相关，小于0的时候表示两者负相关），而除以标准差后，Pearson的值范围为[-1,1]。当两个变量的线性关系增强时，相关系数趋于1或-1，正负号指向正负相关关系。

皮尔森相关系数是一种最简单的，能帮助理解特征和响应变量之间关系的方法，速度快、易于计算，经常在拿到数据(经过清洗和特征提取之后的)之后第一时间就执行。Scipy的pearsonr方法能够同时计算相关系数和p-value

import numpy as np
from scipy.stats import pearsonr

np.random.seed(0)
size = 300
x = np.random.normal(0, 1, size)
print("Lower noise：", pearsonr(x, x + np.random.normal(0, 1, size)))
print("Higher noise：", pearsonr(x, x + np.random.normal(0, 10, size)))


from sklearn.feature_selection import SelectKBest
# 选择K个最好的特征，返回选择特征后的数据
# 第一个参数为计算评估特征是否好的函数，该函数输入特征矩阵和目标向量，输出二元组（评分，P值）的数组，数组第i项为第i个特征的评分和P值。在此定义为计算相关系数
# 参数k为选择的特征个数
SelectKBest(lambda X, Y: array(map(lambda x:pearsonr(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)

Pearson相关系数的一个明显缺陷是，作为特征排序机制，他只对线性关系敏感。如果关系是非线性的，即便两个变量具有一一对应的关系，Pearson相关性也可能会接近 0 。

(2) 斯皮尔曼相关系数

详细解释

Pearson相关系数（Spearman's Rank Correlation Coefficient）是建立在变量符合正态分布的基础上，而Spearman相关系数不假设变量服从何种分布，它是基于等级(rank)的概念去计算变量间的相关性。相当于等级变量之间的皮尔逊相关系数。如果变量是顺序变量(Ordinal Feature)，推荐使用Spearman相关系数。

其中，\(d\) 为两个变量的等级差值， \(n\) 为等级个数。这里举个例子会更好理解，假设我们要探究连续型变量 \(x\) 和 \(y\) 的Spearman相关系数，计算过程如下：

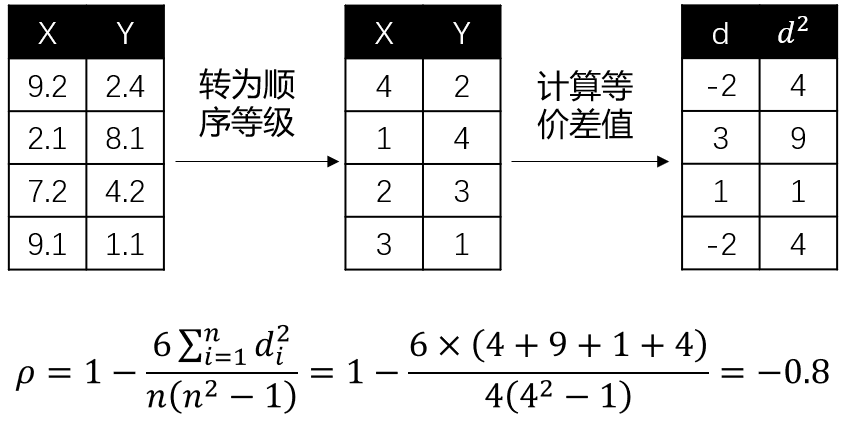
图4: Spearman相关系数

同样地，相关系数趋于1或-1，正负号指向正负相关关系。

2.2 连续型vs类别型

(1) 方差分析

方差分析(Analysis of variance, ANOVA)的目的是检验不同组下的平均数是否存在显著差异。举个例子，我们要判断1,2和3班的同学的数学平均分是否有显著区别？我们能得到，班级为类别型变量，数学分数为连续型变量，如果班级与数学分数有相关性，比如1班同学数学会更好些，则说明不同班的数学平均分有显著区别。为了验证班级与数学分数的相关性，ANOVA会先建立零假设： : (三个班的数学分数没有显著区别)，它的验证方式是看组间方差(Mean Squared Between, MSB)是否大于组内方差(Mean Squared Error, MSE)，如果组间方差>组内方差，说明存在至少一个分布相对于其他分布较远，则可以考虑拒绝零假设。[7]

基于纽约Johnny哥在知乎“什么是ANOVA”的回答[8]，我们举例来试着计算下：

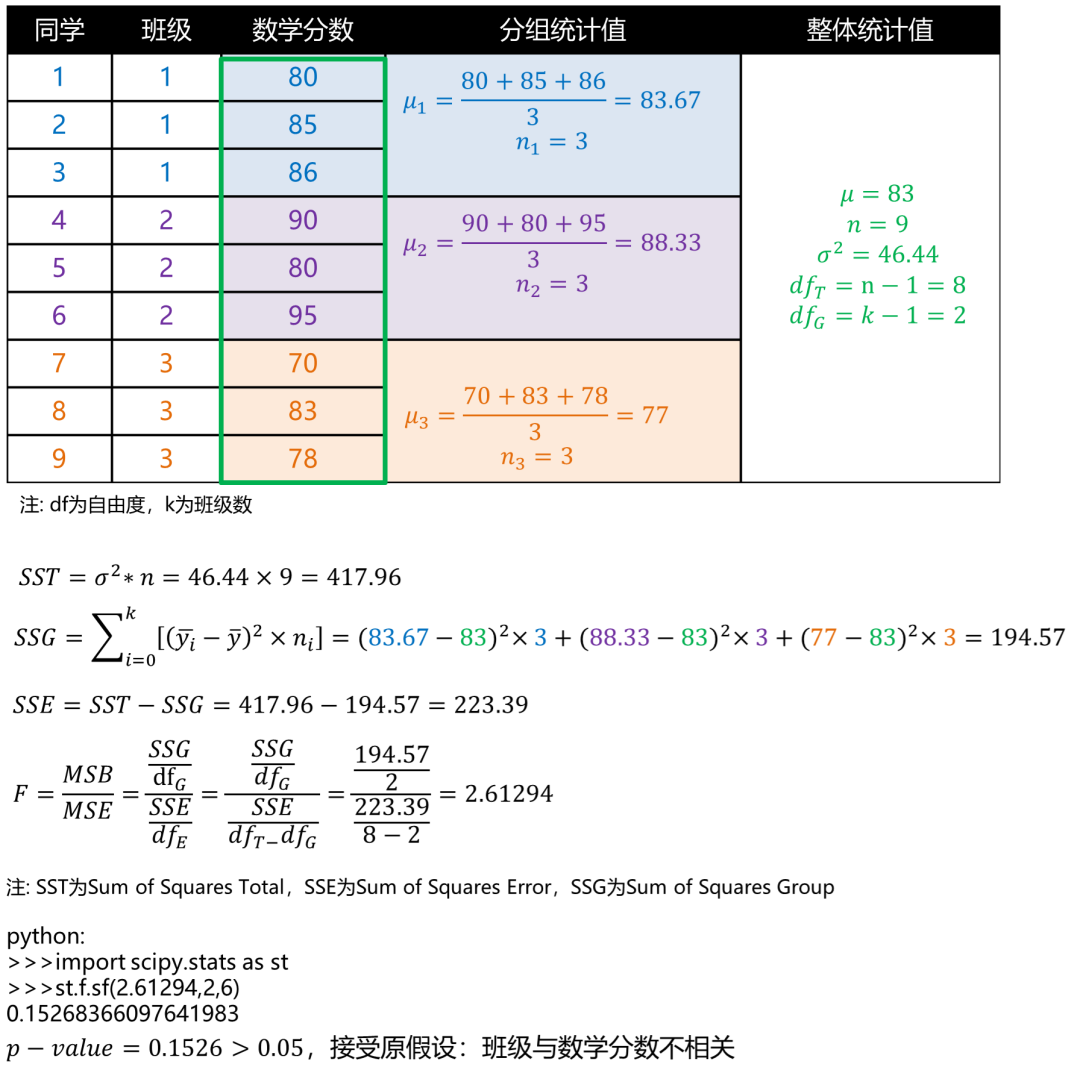
图6: ANOVA分析案例

注意，ANOVA分析前需要满足3个假设: 每组样本具备方差同质性、组内样本服从正态分布，样本间需要独立。[7]

肯德尔等级相关系数(Kendall tau rank correlation coefficient)。

Kendall 秩相关系数是一个非参数性质（与分布无关）的秩统计参数，是用来度量两个有序变量之间单调关系强弱的相关系数，它的取值范围是 \([−1,1]\) ，绝对值越大，表示单调相关性越强，取值为 0 时表示完全不相关。

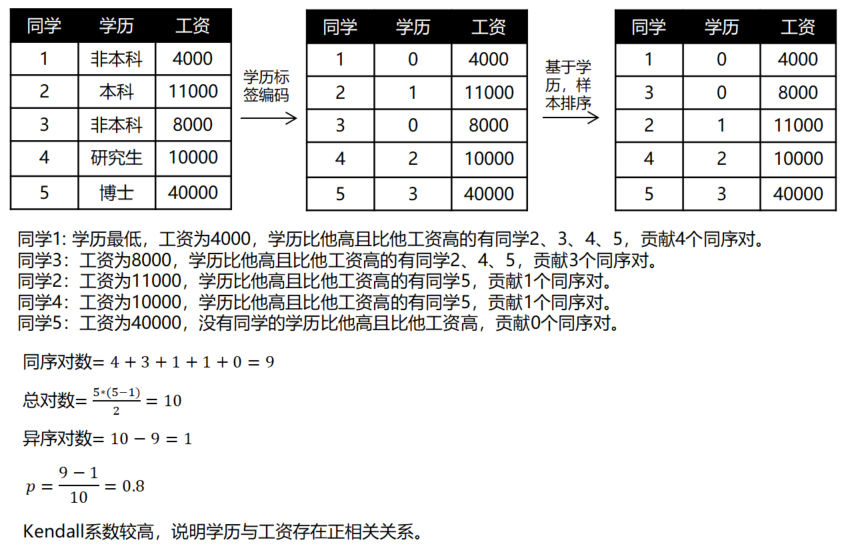
假设我们要评价学历与工资的相关性，Kendall系数会对按学历对样本排序，若排序后，学历和工资排名相同，则Kendall系数为1，两变量正相关。若学历和工资完全相反，则系数为-1，完全负相关。而如果学历和工资完全独立，系数为0。Kendall系数计算公式如下：

\[\tau_a=\frac{c-d}{c+d}=\frac{c-d}{\frac{1}{2}n(n-1)} \]

其中， \(c\) 为同序对， \(d\) 为异序对， \(n\) 为总对数。同样地，我们举例展示下计算过程：

关于变量存在相同取值时的处理方式

\[\tau_b=\frac{c-d}{\sqrt{(c+d+t_x)(c+d+t_y)}} \]

其中，\(c\) 在计算的时候只能算 \(a_i<a_j\) 且 \(b_i<b_j\) 的对数，\(d\) 也只能算 \(a_i<a_j\) 且 \(b_i>b_j\) 的对数 (\(i<j\))；\(t_x\)，\(t_y\) 分别表示变量 \(x\)，\(y\) 取值中序号相同的样本对数排除共同平局的部分 (在下一小节举例说明)。式 \((2)\) 通常又被称为 Tau-b，是实际中应用最广泛的定义。

下面给出一个示例

可以发现，年龄段序号和有效播放序号存在大量的重复数据，因此我们基于式 \((2)\) 来计算：

将样本按年龄段升序排列，相同的年龄段按是否有效播放排序，对年龄段和是否有效播放进行编号，如图 \(2\) 所示；
计算每个样本引入的一致对数和分歧对数，如图 \(2\) 所示 (例如样本 \(4\) 与样本 \(8\sim 10\) 一致)，进而算出 \(c=21\)，\(d=0\)；
计算公共平局的数量 \(t_c\)，公共平局是指 \(a_i=a_j\) 且 \(b_i=b_j\) 的情况 (例如样本 \(1\sim 3\) 互为平局，样本 \(4,5,7\) 互为平局，样本 \(8,9\) 互为平局)，根据图 \(2\) 易知：\(t_c=\frac{3\cdot (3-1)}{2}+\frac{3\cdot (3-1)}{2}+\frac{2\cdot (2-1)}{2}=7\)；
计算只在年龄段平局的数量 \(t_x=\frac{3\cdot (3-1)}{2}+\frac{4\cdot (4-1)}{2}+\frac{2\cdot (2-1)}{2}-t_c=10-7=3\)；
计算只在有效播放平均局的数量 \(t_y=\frac{6\cdot (6-1)}{2}+\frac{4\cdot (4-1)}{2}-t_c=21-7=14\)；
根据式 \((2)\) 得到 \(\tau_b=\frac{21}{\sqrt{(21+3)(21+14)}}=0.725\)；

对应python代码如下：

from scipy.stats import kendalltau
import numpy as np
x=[1,2,3,4,5,6,7,8,9,10]
y=[1,5,2,4,3,7,6,8,9,10]
kendalltau(x,y)
# (0.7777777777777779, 0.0017451191944018172)

x=[1,1,1,2,2,2,2,3,3,4]
y=[1,1,1,1,1,1,2,2,2,2]
kendalltau(x,y)
#(0.72456883730947197, 0.0035417200011750309)

2.3 类别型vs类别型

(1) 卡方验证

经典的卡方检验(Chi-squared Test)是检验类别型变量对类别型变量的相关性。假设自变量有 \(N\) 种取值，因变量有 \(M\) 种取值，考虑自变量等于 \(i\) 且因变量等于 \(j\) 的样本频数的观察值与期望的差距，构建统计量：

\[\chi^2=\sum\frac{(A-E)^2}{E} \]

不难发现，这个统计量的含义简而言之就是自变量对因变量的相关性。用sklearn中feature_selection库的SelectKBest类结合卡方检验来选择特征的代码如下：

from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
iris = load_iris()
X, y = iris.data, iris.target  #iris数据集

#选择K个最好的特征，返回选择特征后的数据
X_new = SelectKBest(chi2, k=2).fit_transform(X, y)

sklearn.feature_selection模块中的类可以用于样本集中的特征选择/维数降低，以提高估计器的准确度分数或提高其在非常高维数据集上的性能

(2) 互信息

参考资料：https://zh.wikipedia.org/wiki/互信息

互信息(Mutual Information)是衡量变量之间相互依赖程度，它的计算公式如下：

\[I(X;Y)=\sum_{y\in Y} \sum_{x \in X}p(x,y)\log\left( \frac{p(x,y)}{p(x)p(y)} \right) \]

其中 \(p(x,y)\) 是 \(X\) 和 \(Y\) 的联合概率密度函数，而 \(p(x)\) 和 \(p(y)\) 分别是\(X\) 和 \(Y\) 的边缘概率密度函数。

它可以转为熵的表现形式

\[\begin{align} I(X;Y)& = H(X) - H(X|Y)\\ &=H(Y)-H(Y|X)\\ &=H(X)+H(Y)-H(X,y)\\ &=H(X,Y)-H(X|Y)-H(Y|X) \end{align} \]

其中 \(H(X|Y)\) 和 \(H(Y|X)\) 是条件熵，\(H(X,Y)\) 是联合熵。当 \(X\) 与 \(Y\) 独立时， \(H(X,Y)=H(X)+H(Y)\) ，则互信息为0。当两个变量完全相同时，互信息最大，因此互信息越大，变量相关性越强。此外，互信息是正数且具有对称性，即 \(I(X;Y)=I(Y;X)\) 。

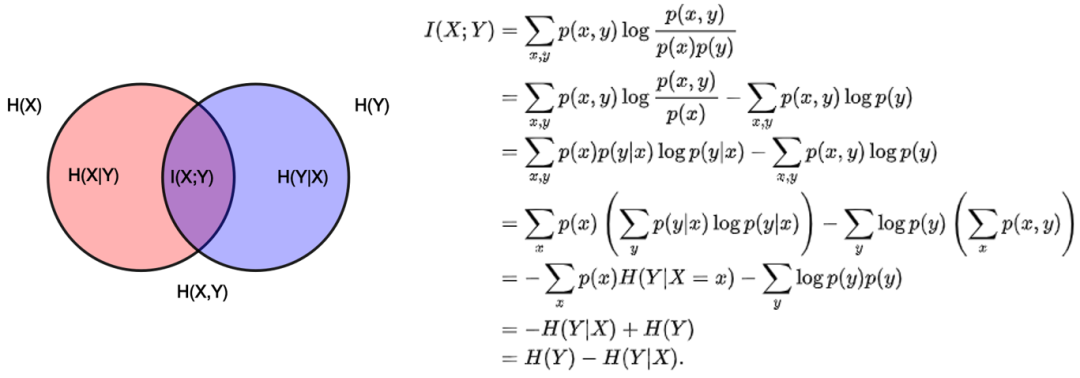
直观地说，如果把熵 \(H(Y)\) 看作一个随机变量于不确定度的量度，那么 \(H(Y|X)\) 就是"在已知 \(X\) 事件后 \(Y\) 事件会发生"的不确定度。于是第一个等式的右边就可以读作“将" \(Y\) 事件的不确定度"，减去 --- "在基于 \(X\) 事件后 \(Y\) 事件因此发生的不确定度"。

这证实了互信息的直观意义为: "因 \(X\) 而有 \(Y\) 事件"的熵( 基于已知随机变量的不确定性) 在" \(Y\) 事件"的熵之中具有多少影响地位( " \(Y\) 事件所具有的不确定性" 其中包含了多少 " \(Y|X\) 事件所具有的不确性" )，意即" \(Y\) 具有的不确定性"有多少程度是起因于 \(X\) 事件;

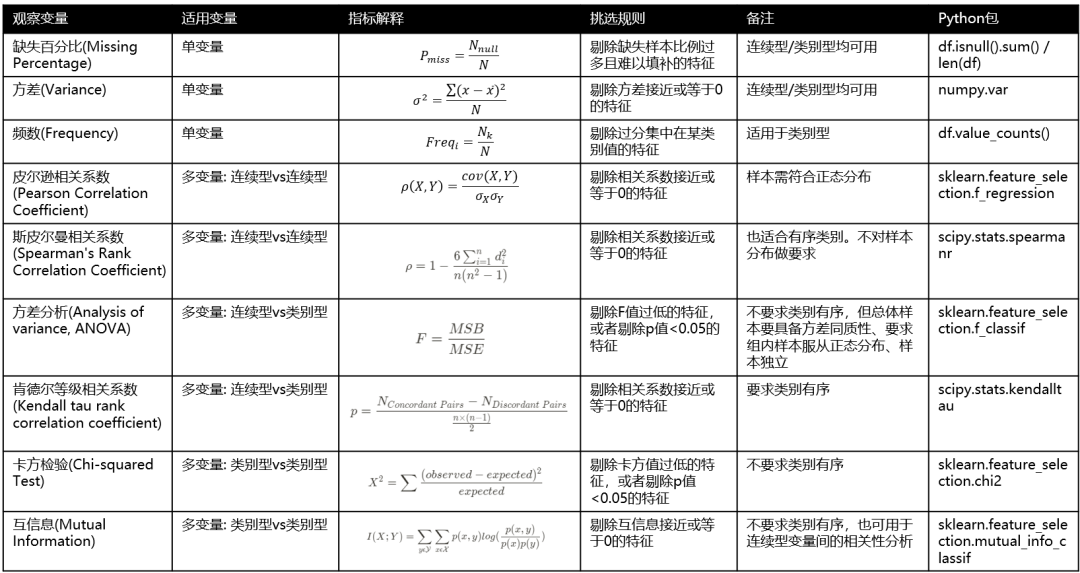
3. 过滤法总结

总结以上内容，如下图所示:

Wrapper

基本思想：基于hold-out方法，对于每一个待选的特征子集，都在训练集上训练一遍模型，然后在测试集上根据误差大小选择出特征子集。需要先选定特定算法，通常选用普遍效果较好的算法，例如Random Forest， SVM， kNN等等。

西瓜书上说Wrapper法应该欲训练什么算法，就选择该算法进行评估
随着学习器（评估器）的改变，最佳特征组合可能会改变

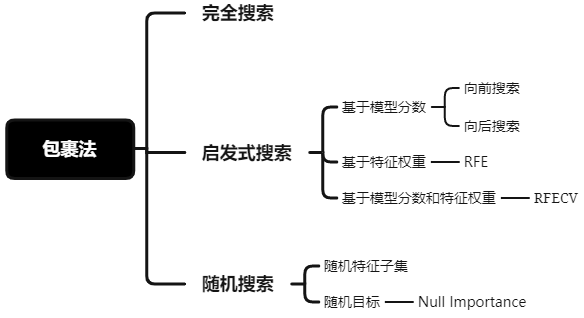
1. 完全搜索

穷举算法 (exhaustive search)，穷举算法是遍历所有可能的组合达到全局最优级，但是计算复杂度是2^n，一般是不太实际的算法。

2. 启发式搜索

2.1 前向/后向搜索

前向搜索说白了就是，每次增量地从剩余未选中的特征选出一个加入特征集中，待达到阈值或者 \(n\) 时，从所有的 \(F\) 中选出效果最好的。过程如下：

初始化特征集 \(F\) 为空。
扫描 \(i\) 从 \(1\) 到 \(n\) 如果第 \(i\) 个特征不在 \(F\) 中，那么特征 \(i\) 和 \(F\) 放在一起作为 \(F_i\) (即 \(F_i=F\cup{i}\) )。在只使用 \(F_i\) 中特征的情况下，利用交叉验证来得到 \(F_i\) 的效果。
从上步中得到的 \(n\) 个 \(F_i\) 中选出效果最好的的 \(F_i\) ,更新 \(F\) 为 \(F_i\) 。
如果 \(F\) 中的特征数达到了 \(n\) 或者预定的阈值（如果有的话），那么输出整个搜索过程中最好的；若没达到，则转到 2，继续扫描。

既然有增量加，那么也会有增量减，后者称为后向搜索。先将 \(F\) 设置为 \(\{1,2,...,n\}\) ，然后每次删除一个特征，并评价，直到达到阈值或者为空，然后选择最佳的 \(F\) 。

这两种算法都可以工作，但是计算复杂度比较大。时间复杂度为：

\[O(n+(n-1)+(n-2)+\dots+1)=O(n^2) \]

2.2 递归特征消除法

递归特征消除简称RFE(Recursive Feature Elimination)，RFE是使用一个基模型进行多轮训练，每轮训练后，消除若干低权值(例如特征权重系数或者特征重要性)的特征，再基于新的特征集进行下一轮训练[1]。RFE使用时，要提前限定最后选择的特征数(n_features_to_select)，这个超参很难保证一次就设置合理，因为设高了，容易特征冗余，设低了，可能会过滤掉相对重要的特征。而且RFE只是单纯基于特征权重去选择，没有考虑模型表现，因此RFECV出现了，REFCV是REF + CV(交叉验证)，它的运行机制是：先使用REF获取各个特征的ranking，然后再基于ranking，依次选择[min_features_to_select, len(feature)]个特征数量的特征子集进行模型训练和交叉验证，最后选择平均分最高的特征子集。

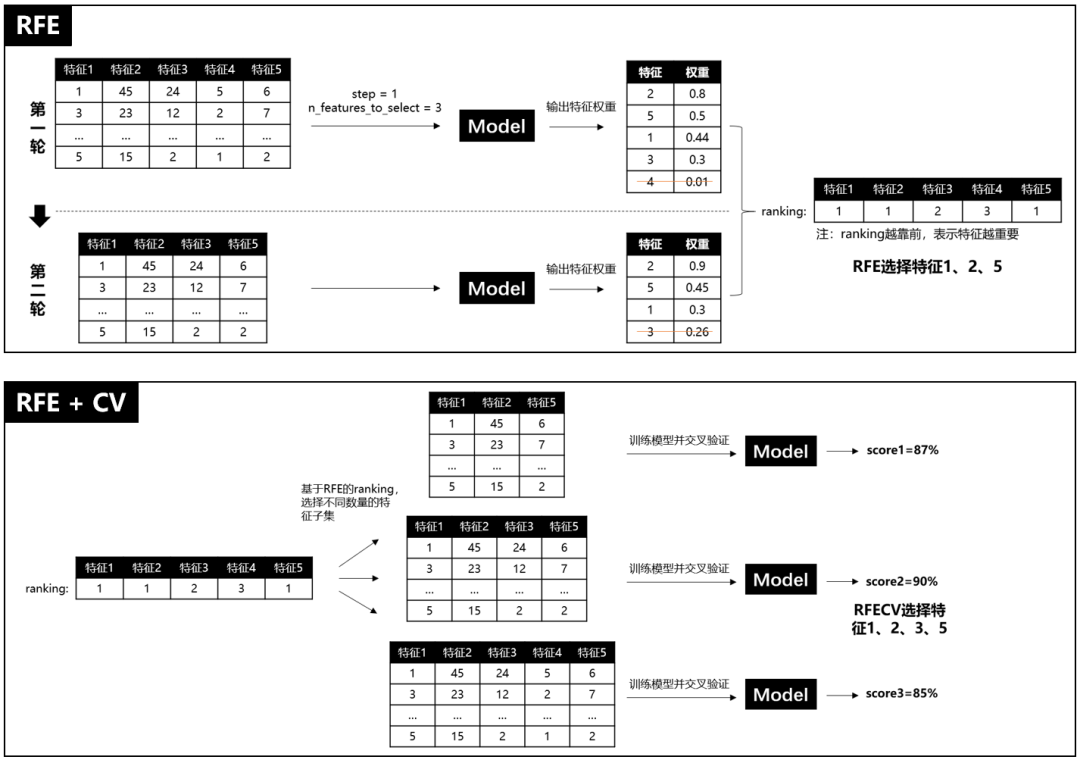
递归消除特征法使用一个基模型来进行多轮训练，每轮训练后通过学习器返回的 coef_ 或者feature_importances_ 消除若干权重较低的特征，再基于新的特征集进行下一轮训练。

使用feature_selection库的RFE类来选择特征的代码如下：

### 生成数据
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=1000,         # 样本个数
                           n_features=25,          # 特征个数
                           n_informative=3,        # 有效特征个数
                           n_redundant=2,          # 冗余特征个数（有效特征的随机组合）
                           n_repeated=0,           # 重复特征个数（有效特征和冗余特征的随机组合）
                           n_classes=8,            # 样本类别
                           n_clusters_per_class=1, # 簇的个数
                           random_state=0)
 
 
### 特征选择
# RFE
from sklearn.svm import SVC
svc = SVC(kernel="linear")
 
 
from sklearn.feature_selection import RFE
rfe = RFE(estimator = svc,           # 基分类器
          n_features_to_select = 2,  # 选择特征个数
          step = 1,                  # 每次迭代移除的特征个数 
          verbose = 0                # 显示中间过程
          ).fit(X,y)
X_RFE = rfe.transform(X)
print("RFE特征选择结果——————————————————————————————————————————————————")
print("有效特征个数 : %d" % rfe.n_features_)
print("全部特征等级 : %s" % list(rfe.ranking_))
 
 
# RFECV
from sklearn.svm import SVC
svc = SVC(kernel="linear")
 
 
from sklearn.model_selection import StratifiedKFold
from sklearn.feature_selection import RFECV
rfecv = RFECV(estimator=svc,          # 学习器
              min_features_to_select=2, # 最小选择的特征数量
              step=1,                 # 移除特征个数
              cv=StratifiedKFold(2),  # 交叉验证次数
              scoring='accuracy',     # 学习器的评价标准
              verbose = 0,
              n_jobs = 1
              ).fit(X, y)
X_RFECV = rfecv.transform(X)
print("RFECV特征选择结果——————————————————————————————————————————————————")
print("有效特征个数 : %d" % rfecv.n_features_)
print("全部特征等级 : %s" % list(rfecv.ranking_))

3. 随机搜索

3.1 随机特征子集

随机选择多个特征子集，然后分别评估模型表现，选择评估分数高的特征子集。

3.2 Null Importance

3年前Kaggle GM Olivier提出Null Importance特征挑选法，最近看完代码，觉得真妙。它成功找出“见风使舵”的特征并剔除了它们，什么是“见风使舵”的特征呢？多见于标识性强或充满噪声的特征，举个例子，如果我们把userID作为特征加入模型，预测不同userID属于哪类消费人群，一个过拟合的模型，可以会学到userID到消费人群的直接映射关系(相当于模型直接记住了这个userID是什么消费人群)，那如果我假装把标签打乱，搞个假标签去重新训练预测，我们会发现模型会把userID又直接映射到打乱的标签上，最后真假标签下，userID“见风使舵”地让都自己变成了最重要的特征。我们怎么找出这类特征呢？Olivier的想法很简单：真正强健、稳定且重要的特征一定是在真标签下特征很重要，但一旦标签打乱，这些优质特征的重要性就会变差。相反地，如果某特征在原始标签下表现一般，但打乱标签后，居然重要性上升，明显就不靠谱，这类“见风使舵”的特征就得剔除掉。

Null Importance的计算过程大致如下:

(1) 在原始数据集运行模型获取特征重要性;

(2) shuffle多次标签，每次shuffle后获取假标签下的特征重要性;

(3) 计算真假标签下的特征重要性差异，并基于差异，筛选特征。

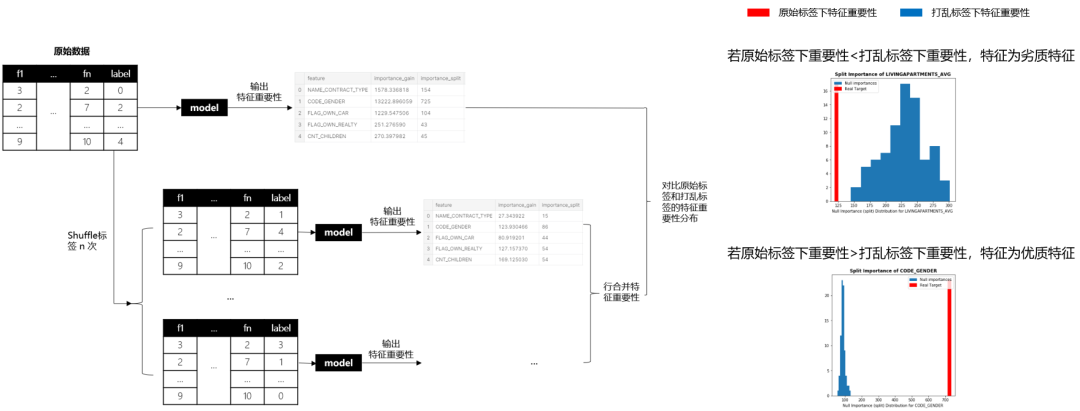
图14: Null Importance的计算过程示意图

在图14我们能知道Null Importance的大致运行流程，但这里补充些细节，其中，重要性你可以选择importance_gain或者importance_split。另外，如图14所示，如果我们要比较原始标签和打乱标签下的特征重要性，Olivier提供了两种比较方法：

第一种：分位数比较。

和1是为了避免和分母为0的情况。输出样例如下：

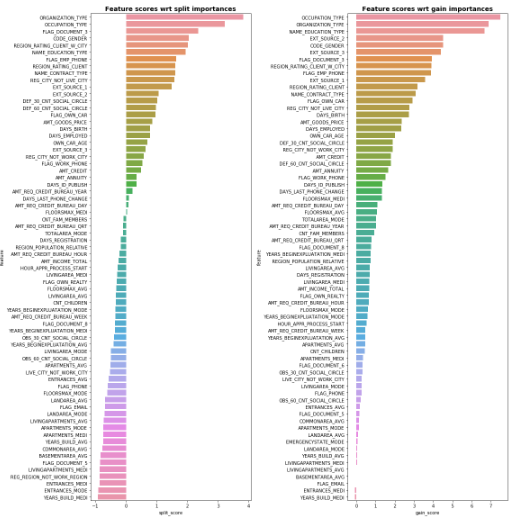
图15: 比较特征重要性分位数

第二种：次数占比比较。

正常来说，单个特征只有1个，之所以作者要求25分位数，是考虑到如果使用时，我们也对原始特征反复训练生成多组特征重要性，所以才就加了25分位数。输出样例如下：

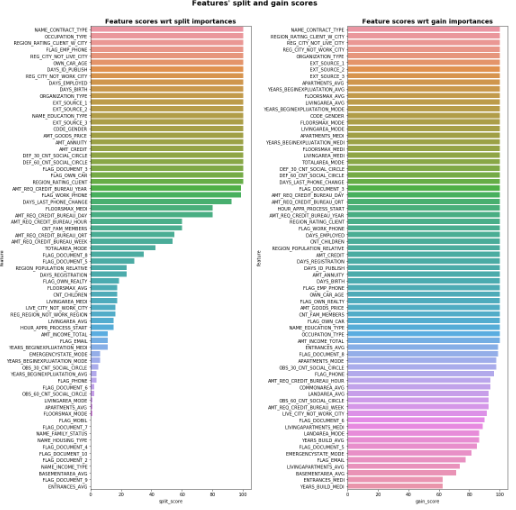
图16: 比较特征重要性次数占比

由上可知，第二种方法得到的特征分数是在0-100范围内，因此Olivier选择在第二种方法上，采用不同阈值去筛选特征，然后评估模型表现。推荐阅读Olivier的开源代码[11]，简单易懂。

4. Wrapper法总结

实际使用中，推荐RFECV和Null Importance，因为他们既考虑了特征权重也考虑了模型表现。

嵌入法

嵌入法: 特征选择被嵌入进学习器训练过程中。不像Wrapper法，特性选择与学习器训练过程有明显的区分。

● 优点: 比Wrapper法更省时省力，把特征选择交给模型去学习。

● 缺点: 增加模型训练负担。

常见的嵌入法有LASSO的L1正则惩罚项、随机森林构建子树时会选择特征子集。嵌入法的应用比较单调，sklearn有提供SelectFromModel[12]，可以直接调用模型挑选特征。参考样例代码[1]如下:

from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import GradientBoostingClassifier
 
 
iris = load_iris()
 
 
# 将待L1惩罚项的逻辑回归作为基模型的特征选择
selected_data_lr = SelectFromModel(LogisticRegression(penalty='l1', C = 0.1, solver = 'liblinear'), max_features = 3).fit_transform(iris.data, iris.target)
 
 
# 将GBDT作为基模型的特征选择
selected_data_gbdt = SelectFromModel(GradientBoostingClassifier(), max_features = 3).fit_transform(iris.data, iris.target)
 
 
print(iris.data.shape)
print(selected_data_lr.shape)
print(selected_data_gbdt.shape)

基于惩罚项的特征选择法：

通过L1正则项来选择特征：L1正则方法具有稀疏解的特性，因此天然具备特征选择的特性。

from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression

#带L1惩罚项的逻辑回归作为基模型的特征选择   
SelectFromModel(LogisticRegression(penalty="l1", C=0.1)).fit_transform(iris.data, iris.target)

要注意，L1没有选到的特征不代表不重要，原因是两个具有高相关性的特征可能只保留了一个，如果要确定哪个特征重要应再通过L2正则方法交叉检验。

from sklearn.feature_selection import SelectFromModel

#带L1和L2惩罚项的逻辑回归作为基模型的特征选择   
#参数threshold为权值系数之差的阈值   
SelectFromModel(LR(threshold=0.5, C=0.1)).fit_transform(iris.data, iris.target)

基于学习模型的特征排序

这种方法的思路是直接使用你要用的机器学习算法，针对每个单独的特征和响应变量建立预测模型。假如某个特征和响应变量之间的关系是非线性的，可以用基于树的方法（决策树、随机森林）、或者扩展的线性模型等。基于树的方法比较易于使用，因为他们对非线性关系的建模比较好，并且不需要太多的调试。但要注意过拟合问题，因此树的深度最好不要太大，再就是运用交叉验证。通过这种训练对特征进行打分获得相关性后再训练最终模型。

在波士顿房价数据集上使用sklearn的随机森林回归给出一个单变量选择的例子：

from sklearn.cross_validation import cross_val_score, ShuffleSplit
from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestRegressor

#加载波士顿房价作为数据集
boston = load_boston()
X = boston["data"]
Y = boston["target"]
names = boston["feature_names"]

#n_estimators为森林中树木数量，max_depth树的最大深度
rf = RandomForestRegressor(n_estimators=20, max_depth=4)
scores = []
for i in range(X.shape[1]):
    #每次选择一个特征，进行交叉验证，训练集和测试集为7:3的比例进行分配，
    #ShuffleSplit()函数用于随机抽样（数据集总数，迭代次数，test所占比例）
    score = cross_val_score(rf, X[:, i:i+1], Y, scoring="r2",
                               cv=ShuffleSplit(len(X), 3, .3))
    scores.append((round(np.mean(score), 3), names[i]))

#打印出各个特征所对应的得分
print(sorted(scores, reverse=True))

输出结果：

[(0.64300000000000002, 'LSTAT'), (0.625, 'RM'), (0.46200000000000002, 'NOX'), (0.373, 'INDUS'), (0.30299999999999999, 'TAX'), (0.29799999999999999, 'PTRATIO'), (0.20399999999999999, 'RAD'), (0.159, 'CRIM'), (0.14499999999999999, 'AGE'), (0.097000000000000003, 'B'), (0.079000000000000001, 'ZN'), (0.019, 'CHAS'), (0.017999999999999999, 'DIS')]

posted @ 2024-08-27 09:04 Un-Defined 阅读(36) 评论(0) 编辑收藏举报

刷新页面返回顶部

UnDefined

特征选择

特征选择

一般流程

三大类方法

过滤法

1. 单变量

2. 多变量

2.1 连续型vs连续型

(1) Pearson相关系数

(2) 斯皮尔曼相关系数

2.2 连续型vs类别型

(1) 方差分析

(2) 肯德尔等级相关系数

2.3 类别型vs类别型

(1) 卡方验证

(2) 互信息

3. 过滤法总结

Wrapper

1. 完全搜索

2. 启发式搜索

2.1 前向/后向搜索

2.2 递归特征消除法

3. 随机搜索

3.1 随机特征子集

3.2 Null Importance

4. Wrapper法总结

嵌入法

基于惩罚项的特征选择法：

基于学习模型的特征排序

公告