XGBoost

XGBoost

参考资料：

目标函数

\[Obj^{(t)}=\sum_{i=1}^n l(y_i, \hat{y}_i^{(t-1)}+f_t(x_i)) + \Omega (f_t) \]

根据泰勒展开： \(f(x+\Delta x) \simeq f(x) + f'(x)\Delta x + \frac{1}{2} f''(x)\Delta x^2\)

\[Obj^{(t)} \simeq \sum_{i=1}^n \left [l(y_i, \hat{y}_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i) \right ] + \Omega (f_t)\\ \]

其中

\[g_i=\partial_{\hat{y}^{(t-1)}}l(y_i, \hat{y}^{(t-1)}),h_i=\partial^2_{\hat{y}^{(t-1)}} l(y_i,\hat{y}^{(t-1)}) \]

  • 泰勒展开中的 \(x\) 对应目标函数中的 \(\hat{y}^{(t-1)}\)
  • \(\Delta x\) 对应 新增加的目标函数 \(f_t(x_i)\)
  • \(f\) 对 \(x\) 求导，就是 \(Obj^{(t)}\) 对 \(\hat{y}^{(t-1)}\) 求导。

所以目标函数除去常数项，得到

\[\sum_{i=1}^n \left [ g_i f_t(x_i) + \frac{1}{2}h_if_t^2(x_i) \right] + \Omega(f_t) \]

正则项

设 \(T\) 是叶子节点的个数， \(q(x)\) 表示样本 \(x\) 在某个叶子节点上， \(w_q(x)\) 是该节点的打分，即该样本的模型预测值。

\[\Omega(f_t)=\gamma T + \frac{1}{2}\sum_{j=1}^T w_j^2 \]

通过对 \(w\) 进行 \(L_2\) 正则化，相当于针对每个叶结点的得分增加 \(L_2\) 平滑，目的是为了避免过拟合。

\[\begin{align} Obj^{(t)} & \simeq \sum_{i=1}^n \left [ g_i f_t(x_i) + \frac{1}{2}h_if_t^2(x_i) \right] + \Omega(f_t)\\ & = \sum_{i=1}^n \left [ g_i w_q(x_i) + \frac{1}{2}h_i w_q^2(x_i) \right] + \gamma T + \frac{1}{2}\sum_{j=1}^T w_j^2\\ &=\sum_{j=1}^T \left [ (\sum_{i\in I_j} g_i) w_j + \frac{1}{2}(\sum_{i \in I_j} h_i+\lambda) w_j^2 \right ] + \gamma T \end{align} \]

其中 \(I_j\) 被定义为每个叶节点 \(j\) 上面样本下标的集合 \(I_j=\{i|q(x_i)=j\}\) ， \(g\) 是一阶导数， \(h\) 是二阶导数。这一步是由于xgboost目标函数第二部分加了两个正则项，一个是叶子节点个数(\(T\))，一个是叶子节点的分数(\(w\))。

定义

\[G_j=\sum_{i\in I_j} g_i, H_j = \sum_{i\in I_j} h_i \]

简化公式为

\[\begin{align} Obj^{(t)} &=\sum_{j=1}^T \left [ (\sum_{i\in I_j} g_i) w_j + \frac{1}{2}(\sum_{i \in I_j} h_i+\lambda) w_j^2 \right ] + \gamma T\\ &=\sum_{j=1}^T \left[ G_jw_j + \frac{1}{2}(H_j+\lambda)w_j^2 \right] + \gamma T \end{align} \]

对 \(w_j\) 求导等于0，得到当 \(w_j^*=-\frac{G_j}{H_j+\lambda}\) 。带入 \(Obj\) ，得到

\[Obj=-\frac{1}{2}\sum_{j=1}^T\frac{G_j^2}{H_j+\lambda} + \gamma T \]

\(Obj\) 代表了当我们指定一个树的结构的时候，我们在目标上面最多减少多少。我们可以把它叫做结构分数(structure score)

分裂节点

每一节点都遍历所有的特征，比如年龄、性别等等，然后对于某个特征，先按照该特征里的值进行排序，然后线性扫描该特征进而确定最好的分割点，最后对所有特征进行分割后，我们选择所谓的增益Gain最高的那个特征，而Gain如何计算呢？

\(Obj\) 中的 \(\frac{G_j^2}{H_j + \lambda}\) 表示叶子结点 \(j\) 对当前模型损失度的贡献，由此得到

\[Gain=\frac{1}{2}\left [ \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L+G_R)^2}{H_L + H_R + \lambda} \right ] - \gamma \]

上式表示 左子树的分数 + 右子树的分数 - 不分割我们可以拿到的分数。 \(\gamma\) 表示加入新叶子节点引入的复杂度代价。当引入的分割带来的增益小于一个阀值 \(\gamma\) 的时候，则忽略这个分割。

对于所有的特征x，我们只要做一遍从左到右的扫描就可以枚举出所有分割的梯度和GL和GR。然后用计算Gain的公式计算每个分割方案的分数就可以了。具体做法如下图所示。

image-20240314105907594

树节点划分算法 - Approximate Algorithm

然而，当落实到具体工程上，数据不能完全装入内存时，就不可能有效地做到这一点。同样的问题也出现在分布式环境中。为了支持这两者情况，一种近似算法如下所示。

image-20240314110106181

该算法首先根据特征分布的百分位数提出候选分裂点。然后，算法将连续特征映射到由这些候选点分割的桶中，汇总统计信息，并根据汇总的统计信息在提议中找到最佳解。

该算法有两个变种，取决于何时提出proposal。全局方法在树构建的初始阶段提出所有候选分裂，并在所有级别上使用相同的proposal进行分裂查找。局部方法在每次分裂后重新提出建议。全局方法所需的proposal步骤比局部方法少。然而，通常全局proposal需要更多的候选点，因为在每次分裂后候选点没有经过细化。局部proposal在分裂后对候选点进行细化，可能更适用于深层树。

稀疏值处理

输入 \(x\) 的稀疏性，可能由这些原因造成：1）数据中存在缺失值；2）统计数据中频繁出现零值；以及，3）特征工程中的人为特征编码等。当 \(x\) 中的值缺失时，XGBoost 将实例分类到默认方向。如算法 3 所示。关键改进是只访问非缺失条目 \(I_k\)。

image-20240314142712671

分块并行

在建树的过程中，最耗时是找最优的切分点，而这个过程中，最耗时的部分是将数据排序。为了减少排序的时间，提出Block结构存储数据。

  • Block中的数据以稀疏格式CSC进行存储
  • Block中的特征进行排序（不对缺失值排序）
  • Block 中特征还需存储指向样本的索引，这样才能根据特征的值来取梯度。
  • 一个Block中存储一个或多个特征的值

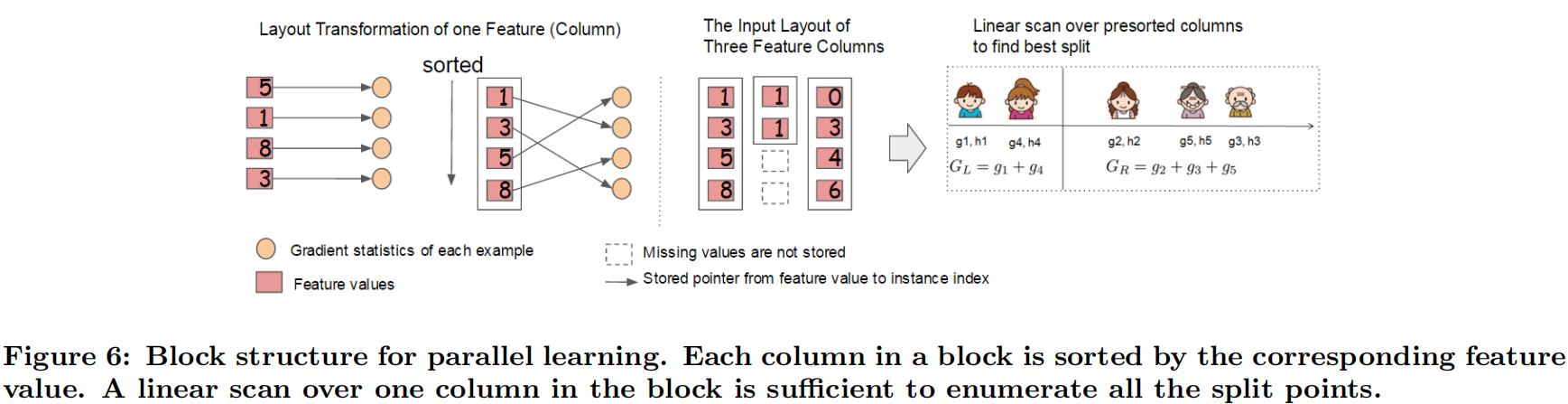
image-20240314190506883

只需在建树前排序一次，后面节点分裂时可以直接根据索引得到梯度信息。

  • 在Exact greedy算法中，将整个数据集存放在一个Block中。这样，复杂度从原来的 \(O(Kd\|x\|_0\log n)\) 降为 \(O(Kd\|x\|_0+\|x\|_0\log n)\) ，其中 \(d\) 为树的最大深度， \(K\) 为树的数量， \(\|x\|_0\) 为训练集中非缺失值的个数。这样，Exact greedy算法就省去了每一步中的排序开销。
  • 在近似算法中，使用多个Block，每个Block对应原来数据的子集。不同的Block可以在不同的机器上计算。该方法对Local策略尤其有效，因为Local策略每次分支都重新生成候选切分点。复杂度从原来的 \(O(Kd\|x\|_0\log q)\) 降低为 \(O(Kd\|x\|_0+\|x\|_0\log B)\) 。其中 \(q\) 是候选分裂点的数量， \(B\) 为每个Block中最大的行数。 \(q\) 一般取值在32到100之间，因此可以考虑省去的 \(\log q\) 。

Block结构还有其它好处，数据按列存储，可以同时访问所有的列，很容易实现并行的寻找分裂点算法。此外也可以方便实现之后要讲的out-of score计算。

缺点是空间消耗大了一倍。

关于时间复杂度

如果我们不使用block结构时，即采用原始的稀疏精确算法时。为了在每一个节点node找到最优的分割，我们需要对每一个特征进行排序。则每层layer的时间复杂度非常粗略地近似 \(O\left(\|\mathbf{x}\|_0 \log n\right)\) : 这是因为，如果对于特征 \(1 \leq i \leq m\) ，每个特征 \(i\) 有 \(\|\mathbf{x}\|_{0 i}\) 非零值，然后，在每一层我们需要排序，且每个特征最多有 \(n\) 个 (即样本为 \(n\) )，因为所有特征的长度为 \(\sum_{i=1}^m\|\mathbf{x}\|_{0 i}=\|\mathbf{x}\|_0\) ，在这种情况下，排序时间不超过 \(O\left(\|\mathbf{x}\|_0 \log n\right.\) )(注：快排的时间复杂度为 \(n \log n\) )。在此基础上，乘以 \(K\) 个树和 \(d\) 层，因此时间复杂度为 \(O\left(K d\|\mathbf{x}\|_0 \log n\right)\) 。

如果我们使用block结构时，在一开始我们就已经对特征进行了排序，不需要在每个节点都排序。正如作者强调的，这时候时间复杂度降到了 \(O\left(K d\|\mathbf{x}\|_0\right)\) ，这是因为，我们对block扫描一遍时就可以得到各个节点的最优切分。再加上一开始排序的复杂度为 \(O\left(\|\mathbf{x}\|_0 \log B\right)\) ，(按照意义，这里 \(B\) 就是 \(n\) )。因此，总时间复杂度为 \(O\left(K d\|x\|_0+\|x\|_0 \log B\right)\) 。

缓存优化

使用Block结构的一个缺点是取梯度的时候，是通过索引来获取的，而这些梯度的获取顺序是按照特征的大小顺序的。这将导致非连续的内存访问，可能使得CPU cache缓存命中率低，从而影响算法效率。

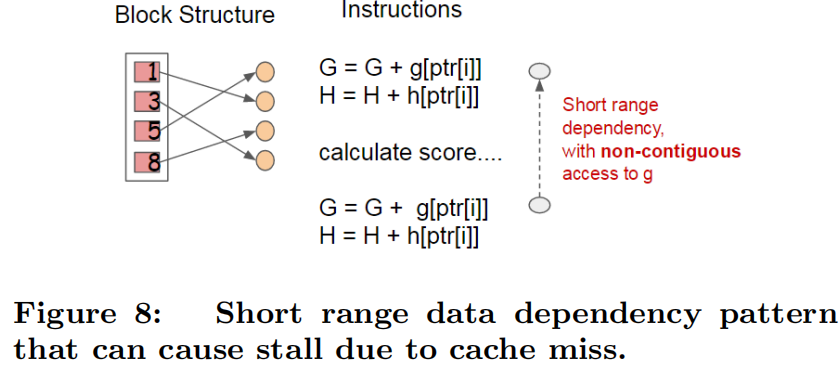
image-20240319124653080

因此，对于exact greedy算法中, 使用缓存预取。具体来说，对每个线程分配一个连续的buffer，读取梯度信息并存入Buffer中（这样就实现了非连续到连续的转化），然后再统计梯度信息。该方式在训练样本数大的时候特别有用，见下图：

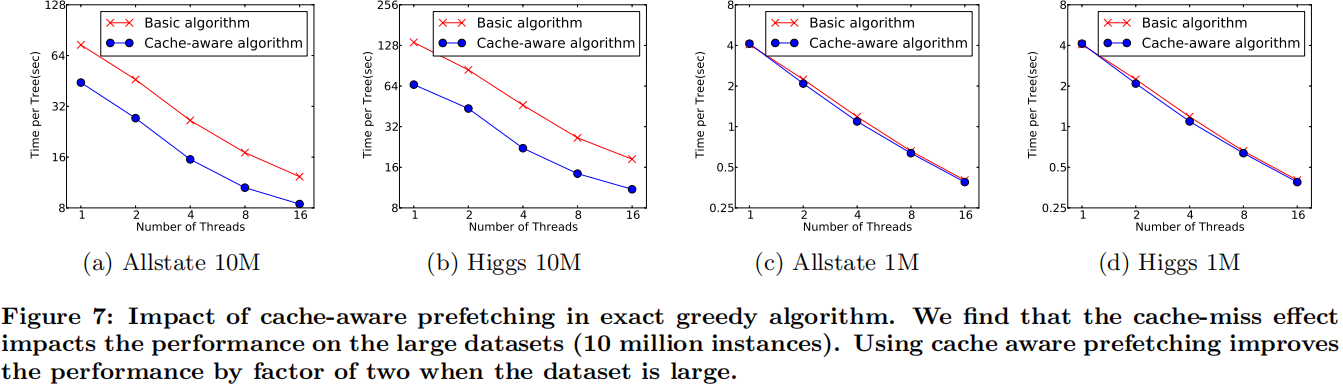
image-20240319125144011

在approximate 算法中，对Block的大小进行了合理的设置。定义Block的大小为Block中最多的样本数。设置合适的大小是很重要的，设置过大则容易导致命中率低，过小则容易导致并行化效率不高。经过实验，发现2^16比较好。

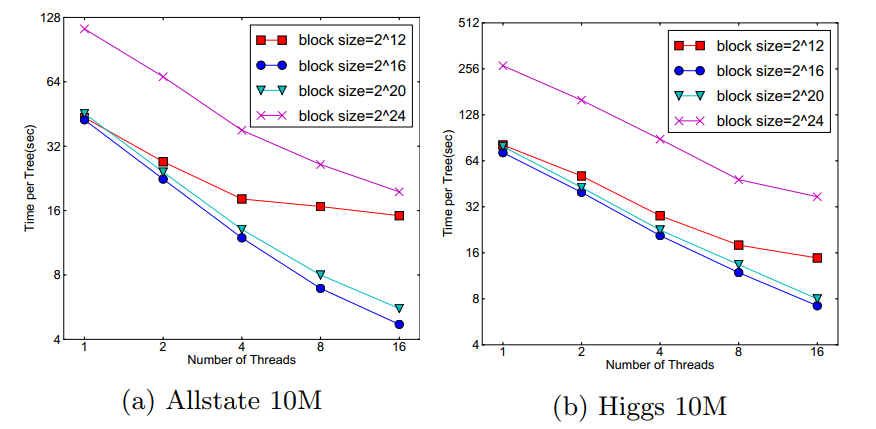
XGBoost-cache-aware-access-approximate-algorithm

Blocks for Out-of-core Computation

当数据量太大不能全部放入主内存的时候，为了使得out-of-core计算称为可能，将数据划分为多个Block并存放在磁盘上。计算的时候，使用独立的线程预先将Block放入主内存，因此可以在计算的同时读取磁盘。但是由于磁盘IO速度太慢，通常更不上计算的速度。因此，需要提升磁盘IO的销量。Xgboost采用了2个策略：

  • Block压缩（Block Compression）：将Block按列压缩（LZ4压缩算法？），读取的时候用另外的线程解压。对于行索引，只保存第一个索引值，然后只保存该数据与第一个索引值之差(offset)，一共用16个bits来保存offset，因此，一个block一般有2的16次方个样本。

  • Block拆分（Block Sharding）：将数据划分到不同磁盘上，为每个磁盘分配一个预取（pre-fetcher）线程，并将数据提取到内存缓冲区中。然后，训练线程交替地从每个缓冲区读取数据。这有助于在多个磁盘可用时增加磁盘读取的吞吐量。

步长

XGBoost加入了步长 \(\eta\)（有的也叫收缩率Shrinkage），用于防止过拟合

\[\hat{y}_i^t=\hat{y}_i^{t-1}+\eta f_t(x_i) \]

通常步长 \(\eta\) 取值为0.1。当然GBDT也可以采用这个。

行、列抽样

XGBoost借鉴随机森林也使用了列抽样(在每一次分裂中使用特征抽样)，进一步防止过拟合，并加速训练和预测过程。

此外，在实现中还有行抽样（样本抽样）。

关于八股

XGBoost 和 GBDT的区别和联系：

  • GBDT是机器学习算法，XGBoost是该算法的工程实现。
  • 在使用 CART 作为基分类器时，XGBoost 显式地加入了正则项来控制模型的复杂度，有利于防止过拟合，从而提高模型的泛化能力。
  • GBDT在模型训练时只使用了代价函数的一阶导数信息，XGBoost 对代价函数进行二阶泰勒展开，可以同时使用一阶和二阶导数。
  • 传统的 GBDT 采用 CART 作为基分类器，XGBoost 支持多种类型的基分类器，比如线性分类器。
  • 传统的 GBDT在每轮迭代时使用全部的数据，XGBoost则采用了与随机森林相似的策略，支持对数据进行采样。
  • 传统的 GBDT没有设计对缺失值进行处理，XGBoost能够自动学习出缺失值的处理策略。
  • XGBoost工具支持并行。当然这个并行是在特征的粒度上，而非tree粒度，因为本质还是boosting算法。

XGBoost为什么快

  • 当数据集大的时候使用近似算法
  • Block与并行
  • CPU cache 命中优化
  • Block预取、Block压缩、Block Sharding等

XGBoost 防止过拟合的方法

  • 目标函数的正则项， 叶子节点数+叶子节点数输出分数的平方和 \(\Omega(f_t)=\gamma T + \frac{1}{2}\sum_{j=1}^{T}{w_j^2}\)
  • 行抽样和列抽样：训练的时候只用一部分样本和一部分特征
  • 可以设置树的最大深度
  • \(\eta\): 可以叫学习率、步长或者shrinkage
  • Early stopping：使用的模型不一定是最终的ensemble，可以根据测试集的测试情况，选择使用前若干棵树
posted @ 2024-08-27 09:01  Un-Defined  阅读(9)  评论(0)  编辑  收藏  举报