[论文阅读] Anomaly detection with domain adaptation

Anomaly detection with domain adaptation

3. Methodology

Problem Statement

我们研究了在领域适应设置中的半监督异常检测问题。在训练阶段，学习算法可以访问 \(n\) 个数据点 \(\left\{\left(\boldsymbol{x}_{s r c}^{(i)}, y_{s r c}^{(i)}\right)\right\}_{i=1}^n \in(X \times Y)^n\)，这些数据点是从源域 \(\mathcal{D}_S\) 中独立同分布采样得到的，以及有限的目标数据点 \(\left\{\left(\boldsymbol{x}_{t g t}^{(j)}, y_{t g t}^{(j)}\right)\right\}_{j=1}^{n_t} \in(X \times Y)^{n_t}\)，这些数据点是从目标域 \(\mathcal{D}_t\) 中独立同分布采样得到的（其中 \(n_t\) 很小且 \(n_t \ll n\) ）。设 \(y=0(y=1)\) 表示正常（异常）。在半监督异常检测中，我们只能访问正常数据，即 \(y_{s r c}^{(i)}=0\) 且 \(y_{t g t}^{(j)}=0, \forall i, j\)。目标是构建一个在目标域中的异常评分函数 \(A\left(\boldsymbol{x}_{t g t}\right): X \rightarrow a \in \mathbb{R}\)。测试集包含目标域数据的正常和异常样本。学习模型的评估指标是根据测试样本的真实标签和异常分数计算的ROC曲线下的面积，即AUROC。

3.1. Invariant Representations Extraction by Adversarial Learning

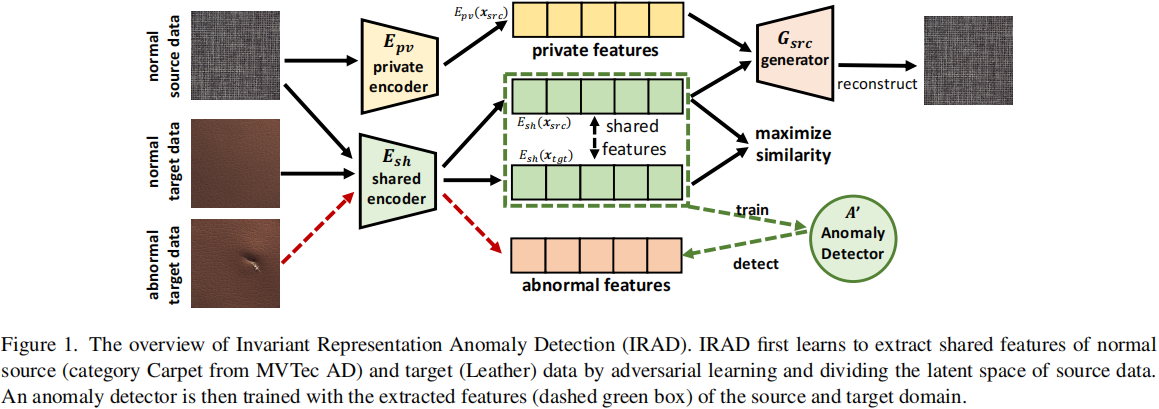
学习领域不变特征是领域适应问题的主流解决方案 [5, 10, 34]。IRAD包括一个共享编码器 \(E_{s h}\)，用于提取源域和目标域数据之间的共同特征，这是先前工作中常用的方法 \([5,10]\)。为了实现对共享和特定域组件的适当分割，IRAD还在源域中训练一个私有编码器 \(E_{p v}\)，以从领域共享编码中移除源特定信息（见第3.2节）。为确保学到的组件实际包含有用信息，我们还引入了一个生成器，将潜在空间映射到源域的数据空间 \(G_{s r c}\)。生成器 \(G_{s r c}\)，编码器 \(E_{s h}\) 和 \(E_{p v}\) 通过源域中的鉴别器 \(D_{s r c}\) 进行对抗训练。对抗损失如下：

\[\begin{array}{l} \min _{\left\{E_{s h}, E_{p v}, G_{s r c}\right\}} \max _{D_{s r c}} V_{s r c}\left(D_{s r c}, G_{s r c}, E_{p v}, E_{s h}\right)=\\ \mathbb{E}_{\boldsymbol{x}_{s r c}}\left[\log D_{s r c}\left(\boldsymbol{x}_{s r c}\right)\right]+\mathbb{E}_{\boldsymbol{x}_{s r c}}\left[\log \left(1-D_{s r c}\left(\boldsymbol{x}_{s r c}^{\prime}\right)\right]\right. \\ \quad+\mathbb{E}_{\boldsymbol{x}_{s r c}, \boldsymbol{x}_{t g t}}\left[\log \left(1-D_{s r c}\left(\boldsymbol{x}_{t g t}^{\prime}\right)\right]\right. \\ \quad+\mathbb{E}_{\boldsymbol{x}_{s r c}}\left[\log \left(1-D_{s r c}\left(\boldsymbol{x}_{r n d}\right)\right]\right. \end{array} \tag{1} \]

其中 \(\boldsymbol{x}_{s r c}^{\prime}=G\left(E_{p v}\left(\boldsymbol{x}_{s r c}\right)+E_{s h}\left(\boldsymbol{x}_{s r c}\right)\right)\) 表示源数据的重建； \(\boldsymbol{x}_{t g t}^{\prime}=G\left(E_{p v}\left(\boldsymbol{x}_{s r c}\right)+E_{s h}\left(x_{t g t}\right)\right)\) 表示使用从目标数据提取的共同信息 \(E_{s h}\left(x_{t g t}\right)\) 和源数据的私有编码生成的；\(\boldsymbol{x}_{r n d}=G\left(\boldsymbol{z}+E_{s h}\left(\boldsymbol{x}_{s r c}\right)\right)\) 是使用从随机分布采样得到的变量 \(z\)（经验上我们发现 \(\mathcal{N}(0,1)\) 效果很好）和共享编码 \(E_{s h}\left(\boldsymbol{x}_{s r c}\right)\) 生成的。 \(\boldsymbol{x}_{r n d}\) 的设计是为了避免私有编码器过于强大（错误地）导致源域的所有潜在信息都被 \(E_{p v}\) 编码。通过将随机向量作为输入的一部分，共享编码器通过对抗训练来捕捉源数据的基本信息，使得生成的 \(x_{r n d}\) 接近 \(x_{s r c}\)。我们在第5节进行关于 \(\boldsymbol{x}_{r n d}\) 的消融研究。判别器 \(D_{s r c}\) 被训练用于区分真实源数据 \(x_{s r c}\) 与 \(\boldsymbol{x}_{s r c}^{\prime}, \boldsymbol{x}_{t g t}^{\prime}\) 和 \(\boldsymbol{x}_{r n d}\)。共享编码器 \(E_{s h}, E_{p v}\) 和 \(G_{s r c}\) 被训练以最大化 \(D_{s r c}\) 的错误。在最优情况下，\(\boldsymbol{x}_{s r c}^{\prime}, \boldsymbol{x}_{t g t}^{\prime}\) 和 \(\boldsymbol{x}_{r n d}\) 应该在 \(D_{s r c}\) 方面类似于真实数据 \(\boldsymbol{x}_{s r c}\)。

除了对抗训练外，我们还使用以下循环一致性损失进行优化：

\[l_1=\left\|x_{s r c}-x_{s r c}^{\prime}\right\|_2, \quad l_2=\left\|x_{s r c}-x_{t g t}^{\prime}\right\|_2 \tag{2} \]

第一个损失在源数据空间中强制执行循环一致性属性。第二个确保从目标数据中提取的组件 \(E_{s h}\left(\boldsymbol{x}_{t g t}\right)\) 实际上是共享特征，使它们驻留在与 \(E_{s h}\left(x_{s r c}\right)\) 相同的子空间中。在我们的实验中，循环一致性损失在高维实际图像（例如，在Office-Home数据集中，图像尺寸通常大于 \(300 \times 300\) ）中非常关键。我们推测这是由于 GAN 对于高维数据的训练不稳定导致的 [1]。像直接的循环一致性损失这样的更强信号应该有助于生成器和编码器的优化。

3.2. Split of Private and Shared Components

源数据的共享和私有编码子空间应该是不相似的，因为它们提取 \(\boldsymbol{x}_{s r c}\) 的不同特征。例如，在一个以MNIST（源）和SVHN（目标）为例的领域适应问题，表示为MNIST \(\rightarrow\) SVHN，共享编码应该学习提取与数字相关的信息，而私有编码则预计包含有关数字的风格、大小等方面的组件。为了强制执行这一特性，我们引入了一个优化目标，最小化（规范化后的）共享编码和私有编码之间的相似性，类似于 [5]：

\[l_{d i s}=\left\|E_{s h}\left(\boldsymbol{x}_{s r c}\right)^T E_{p v}\left(\boldsymbol{x}_{s r c}\right)\right\| \tag{3} \]

此外，从两个域中提取的共享编码应该是相似的，因为它们应该捕捉两个域之间的共同信息。因此，我们最小化源数据和目标数据的（规范化后的）共享编码之间的内积的负值：

\[l_{s i m}=-\left\|E_{s h}\left(\boldsymbol{x}_{s r c}\right)^T E_{s h}\left(\boldsymbol{x}_{t g t}\right)\right\| \tag{4} \]

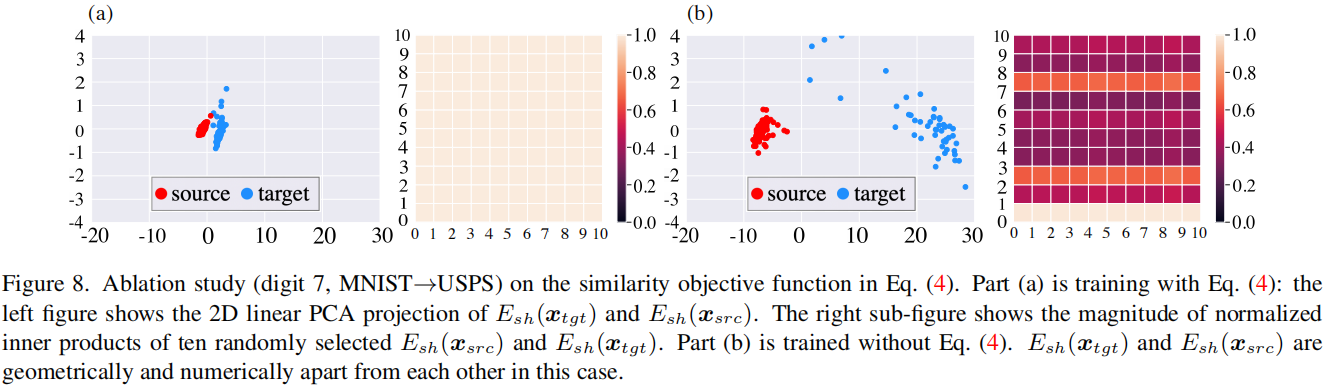
我们在图8中展示了 \(l_{\text {sim }}\) 目标对确保从源数据和目标数据中提取的共享编码之间的接近性是至关重要的。没有 \(l_{\text {sim }}\)，我们观察到源数据和目标数据的共享编码相距太远，这会削弱异常检测算法的性能。关于这一消融研究的更多细节将在第5节中给出。

IRAD的最终目标函数是上述损失的加权和：

\[V_{s r c}+\alpha_1 l_1+\alpha_2 l_2+\beta\left(l_{\text {dis }}+l_{\text {sim }}\right) \]

经验上，我们发现 \(\alpha_1=1, \alpha_2=1, \beta=0.5\) 效果很好。除非另有说明，这些值将在实验中使用。

3.3. Anomaly Detection

在共享编码器训练完成后，我们可以方便地利用现成的异常检测算法 \(A^{\prime}\)，使用从训练集中提取的源数据和目标数据的共享表示来训练一个异常检测模型。一般来说，任何半监督异常检测模型都可以在这里使用。在本文中，我们探讨了在IRAD中使用隔离森林（Isolation Forest，IF）[20] 和一类支持向量机（One-Class SVM，OCSVM）[27] 作为 \(A^{\prime}\) 的选择，分别在后文中表示为 IRAD(IF) 和 IRAD(OC)。关于IF和OCSVM的描述将在下一节中找到。我们选择IF和OCSVM是因为它们是流行且有效的方法，有标准的实现可用 [22]。我们在实验中对IRAD(IF)/IRAD(OC)和纯粹的IF/OCSVM进行了详细比较。

在测试阶段，给定一个测试样本 \(\boldsymbol{x}\)，我们将 \(\boldsymbol{x}\) 编码到源域和目标域之间的共享子空间 \(E_{s h}(\boldsymbol{x})\)。然后，异常得分 \(A(\boldsymbol{x})\) 可以表示为 \(A^{\prime}\left(E_{s h}(\boldsymbol{x})\right)\)。图1概述了IRAD框架的整体情况，其中源域和目标域分别是MVTec AD数据集中的Carpet和Leather。

4. Experimental and Theoretical Results

4.1. MVTec AD Dataset

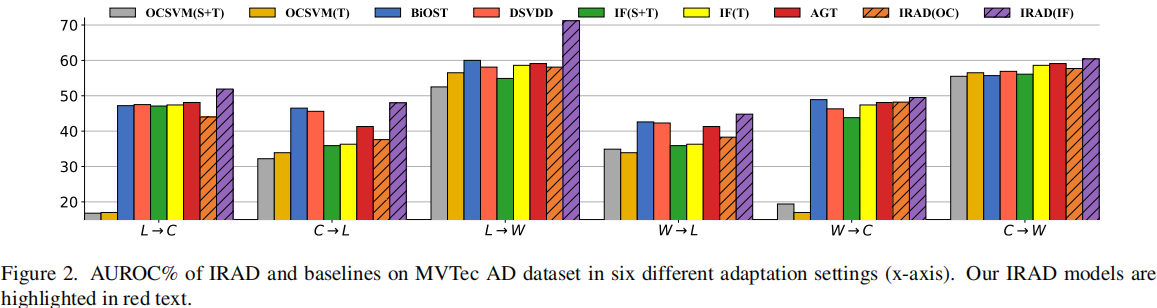
利用MVTec AD中的纹理图案对象构建了一个异常检测领域适应基准，其中包括Carpet（C）、Leather（L）和Wood（W）。例如，假设源域和目标域分别是Carpet和Leather，表示为 C → L。在训练阶段，Carpet的图像和少量Leather的图像可用（来自两个域的图像都是正常的）。测试数据包括正常和异常的Leather图像。

baseline:

• Isolation Forest (IF)：IF (T) 仅使用目标数据进行训练；IF (S+T) 使用源数据和目标数据进行训练。
• One Class Support Vector Machines (OCSVM)：与IF类似，测试了OCSVM的两个变体：OCSVM（T）和OCSVM（S+T）。
• Bidirectional One-Shot Unsupervised Domain Mapping (BiOST)： 是最近在少样本域变换上的研究成果 [7]。BiOST分别为每个域学习一个编码器-生成器对。然后，通过跨域循环映射损失和潜在空间中的KL散度（类似于变分自动编码器（VAE）中的KL散度）训练网络。目标数据示例的异常得分是其重构误差。BiOST是利用跨域转换的方法的代表性基线之一 [15,30]。
• Deep Support Vector Data Description (DSVDD)：
• Data Augmentation (AGT)：通过增强目标域的训练数据，表示为“AGT”。数据通过图像旋转和翻转进行增强，然后在增强后的数据上训练隔离森林。

4.2. Digits Anomaly Detection

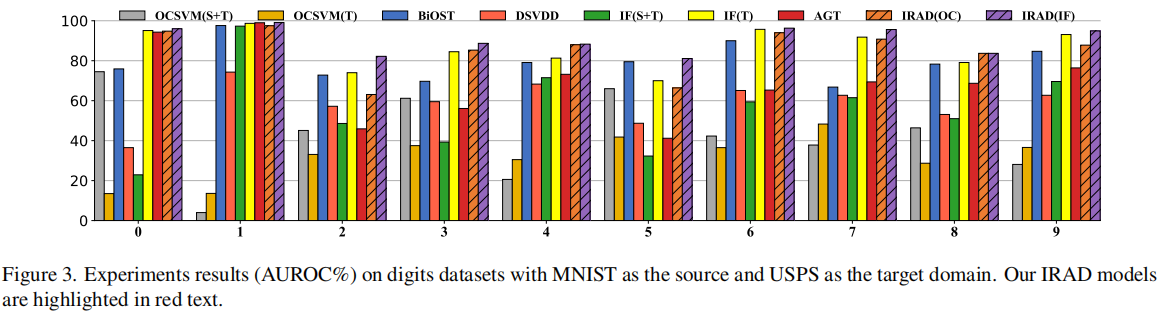
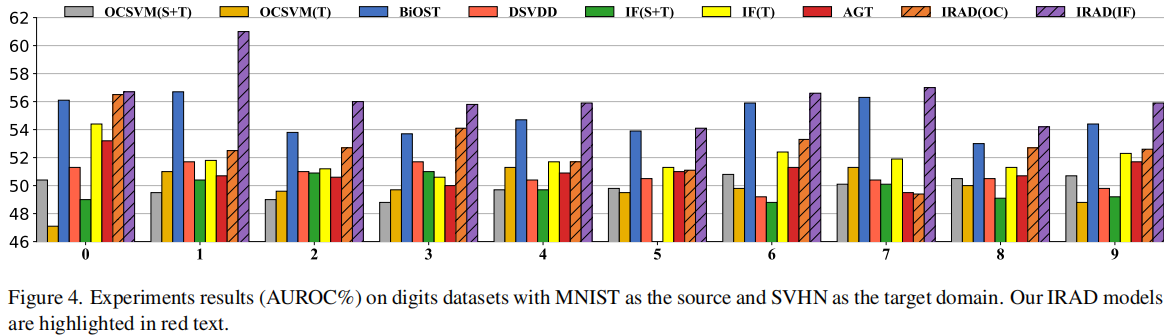
在数字数据集上进行评估，涉及两种适应情景：从MNIST（源域）到USPS（目标域）的适应和从MNIST（源域）到SVHN（目标域）的适应。假设数字0是正常类。在训练阶段，源域（例如MNIST）中的数字0以及目标域（例如USPS）中有限数量的数字0可用（\(n_t = 50\)）。

一个有趣的观察是IF (S+T) 实际上表现比IF (T) 更差。我们推测这是因为MNIST和USPS数字来自相近但仍然不同的分布。MNIST数据实际上向IF的训练添加了噪音，破坏了性能。我们在第4.4节中为这一观察提供了理论解释。

4.3. Objects Recognition Anomaly Detection

我们在两个实验场景下进行测试：Product→Clip Art和Clip Art →Product。在训练集中目标域图像的数量 \(n_t=10\)。

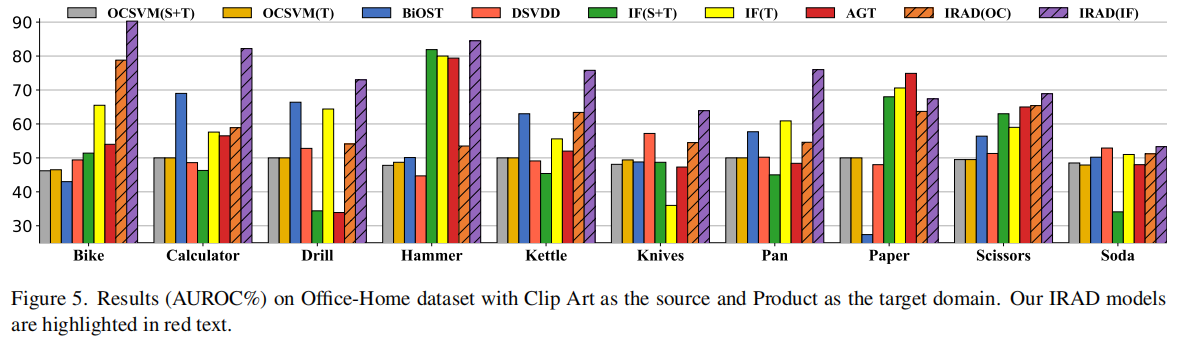
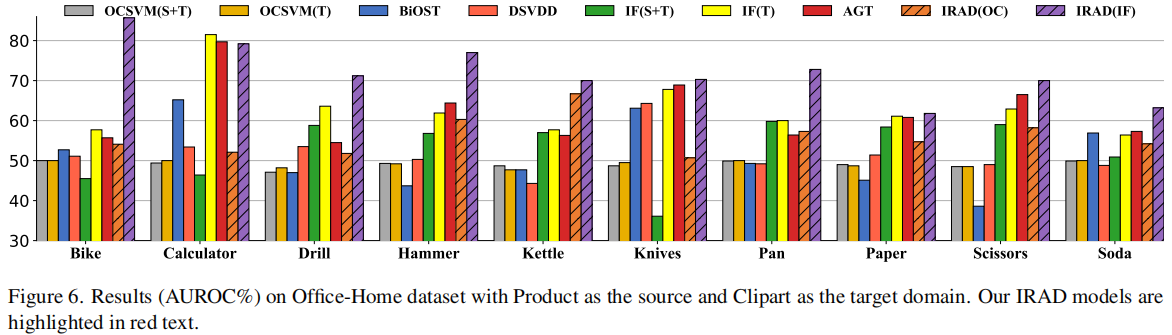
4.4. Bounds for the Joint Error and the Generalization Error

最近关于分类领域自适应的理论研究发现，在源域上最小化经验误差可能对模型在目标域的性能产生不利影响 [34]。我们在领域自适应异常检测中观察到相同的现象，即IRAD的过度训练导致检测的准确性降低，如图7所示。模型性能首先增长，然后在5个epoch后逐渐减少。我们推导了联合误差的信息理论下界（Thm. 1）来解释这一现象。

我们从定义和符号开始。设 \(\mathcal{D}^{Y_S}\) 和 \(\mathcal{D}^{Y_T}\) 分别表示源域和目标域中的边缘标签分布。在IRAD的情况下，由 \(E_{s h}\) 引发的从数据空间 \(X\) 到潜在不变表示空间 \(Z\) 的投影表示为 \(g\)。假设（标签）函数 \(h\) 在两个域之间共享，将不变表示 \(Z\) 映射到预测 \(\hat{Y}\)。对于IRAD， \(h\) 是由在不变表示上学到的IF引发的（IF学到了异常函数）。为了简化证明过程，我们假设异常分数通过应用阈值等方式被转换为分类概率，。

上述过程可以表示为马尔可夫链 \(X \stackrel{g}{\longrightarrow} Z \stackrel{h}{\longrightarrow} \hat{Y}\)[10,34]。设 \(d_{\text {JS }}\) 表示JS距离，它是JS散度的平方根 [8]。设 \(\varepsilon_S(h \circ g)\) 和 \(\varepsilon_T(h \circ g)\) 分别表示学到的模型在源域和目标域中的误差。然后我们有关于联合误差下界的以下定理（定理的证明见附录）：（看不懂就不翻译了）

Theorem 1. Assume the chain is Markov, a lower bound for the joint error on the source and target domains is:

\[\varepsilon_S(h \circ g)+\varepsilon_T(h \circ g) \geq \frac{1}{2} d_{\mathrm{JS}}\left(\mathcal{D}^{Y_S}, \mathcal{D}^{Y_T}\right)^2 \]

Remark: Since the definitions of normal data are different in source and target domains, \(d_{\mathrm{JS}}\left(\mathcal{D}^{Y_S}, \mathcal{D}^{Y_T}\right)>0\). This term is dataset-intrinsic and independent of the learning models. The lower bound explains the phenomenon in Fig. 7: overtraining to minimize \(\varepsilon_S\) actually increases the error on the target domain \(\varepsilon_T\). Learning without adaptation (e.g. IF \((\mathrm{S}+\mathrm{T})\) ) can have small \(\varepsilon_S\) but still large error in the target domain. This lower bound also holds for other domain adaptation anomaly detection methods that use invariant representations. This theorem reveals that to have a well-performing model on the target domain, one needs to balance between learning effective invariant representations for accurate \(\mathrm{AD}\) on the source domain while accommodating the target domain data. This trade-off is hard to avoid and is a consequence of our assumption that the data for \(T\) is insufficient for accurate training of the model. So the best outcome is a balanced trade-off between our learning from \(S\) and making corrections based on our limited sampling of \(T\). We use cross-validation to estimate the optimal number of training epochs as mentioned before.

We also derive an upper bound for the generalization error. Let \(f_S, f_T\) be the true labeling function for the source and target domains respectively. Let \(\widehat{D}_S\) and \(\widehat{D}_T\) denote the empirical source and target distributions from source domain samples \(\mathbf{S}\) and target domain samples \(\mathbf{T}\) of size \(n_t\) :

Theorem 2. For a hypothesis space \(\mathcal{H} \subseteq[0,1]^X, \forall h \in \mathcal{H}\), \(\forall \delta>0\), w.p. at least \(1-\delta\) :

\[\begin{aligned} \varepsilon_T(h) & \leq \widehat{\varepsilon}_S(h)+d_{\tilde{\mathcal{H}}}\left(\widehat{\mathcal{D}}_S, \widehat{\mathcal{D}}_T\right) \\ & +2 \operatorname{Rad}_{\mathbf{S}}(\mathcal{H})+2 \operatorname{Rad}_{\mathbf{S}}(\tilde{\mathcal{H}})+2 \operatorname{Rad}_{\mathbf{T}}(\tilde{\mathcal{H}}) \\ & +\min \left\{\mathbb{E}_{\mathcal{D}_S}\left[\left|f_S-f_T\right|\right], \mathbb{E}_{\mathcal{D}_T}\left[\left|f_S-f_T\right|\right]\right\} \\ & +O\left(\sqrt{\log (1 / \delta) / n_t}\right) \\ \tilde{\mathcal{H}}:= & \left\{\operatorname{sgn}\left(\left|h(\mathbf{x})-h^{\prime}(\mathbf{x})\right|-t\right) \mid h, h^{\prime} \in \mathcal{H}, t \in[0,1]\right\} \end{aligned} \]

\(\operatorname{Rad}_{\mathbf{S}}\) denotes the empirical Rademacher complexity w.r.t. samples \(\mathbf{S}\) (see the formal definition in the appendix).

Remark: this bound is formed by the following components (left to right): (1) empirical error on \(S\), (2) distance between the training sets of \(S\) and \(T\), (3) complexity measures of \(\mathcal{H}\) and \(\tilde{\mathcal{H}}\), (4) differences in labels between source and target, (5) error caused by limited target samples.

5. Discussion

为了更好地理解IRAD的目标函数，我们进行了以下消融研究，通过在训练过程中移除特定术语。首先，我们研究了鼓励源数据和目标数据的共享编码相似性的等式（4）。理想情况下，共享编码\(E_{s h}\left(\boldsymbol{x}_{t g t}\right)\)和\(E_{s h}\left(\boldsymbol{x}_{s r c}\right)\)应该位于相同的区域。为了说明这一点，我们通过线性PCA在图8(a)和图8(b)的左侧子图中将\(E_{s h}\left(\boldsymbol{x}_{t g t}\right)\)和\(E_{s h}\left(\boldsymbol{x}_{s r c}\right)\)在2D中进行可视化。通过等式（4）中的相似性目标函数，\(E_{s h}\left(\boldsymbol{x}_{t g t}\right)\)和\(E_{s h}\left(\boldsymbol{x}_{s r c}\right)\)在潜在空间中靠近（图8(a)）；没有等式（4），\(E_{s h}\left(\boldsymbol{x}_{t g t}\right)\)和\(E_{s h}\left(\boldsymbol{x}_{s r c}\right)\)相距较远（图8(b)）。我们还在图8(a)和图8(b)的右侧子图中绘制了10个 \(E_{s h}\left(\boldsymbol{x}_{t g t}\right)\)和\(E_{s h}\left(\boldsymbol{x}_{s r c}\right)\)之间的标准化内积的大小。结果表明，通过等式（4）进行优化确实使得\(E_{s h}\left(\boldsymbol{x}_{t g t}\right)\)和\(E_{s h}\left(\boldsymbol{x}_{s r c}\right)\)在数值上靠近。

我们进一步研究了等式（2）中的循环一致性损失。我们发现它们在Office-Home数据集的评估中至关重要。在没有这些损失的情况下进行训练可能导致性能下降超过\(10 \%\)。我们使用PCA在2D中可视化了正常和异常目标数据的提取特征，\(E_{s h}\left(\boldsymbol{x}_{n o r}\right)\)和\(E_{s h}\left(\boldsymbol{x}_{a b n}\right)\)。理想情况下，\(E_{s h}\left(\boldsymbol{x}_{n o r}\right)\)和\(E_{s h}\left(\boldsymbol{x}_{a b n}\right)\)应该是分开的，以便检测异常。这是我们在使用完整模型进行训练时观察到的（图9(a)的第一列）。然而，如果没有等式（2）进行优化，编码的正常和异常数据会混合在一起（图9(a)的第二列）。我们还研究了等式（1）中的术语\(\boldsymbol{x}_{r n d}\)。从对抗训练中删除\(\boldsymbol{x}_{r n d}\)导致\(E_{s h}\left(\boldsymbol{x}_{n o r}\right)\)和\(E_{s h}\left(\boldsymbol{x}_{a b n}\right)\)混合在一起（图9(a)的第三列）。我们推测对于高维数据（如图像），鉴别器难以形成有效的决策边界[32]，因此额外的正则化术语\(\left(\boldsymbol{x}_{r n d}\right)\)和目标函数（循环一致性损失）有助于建模正常数据分布。

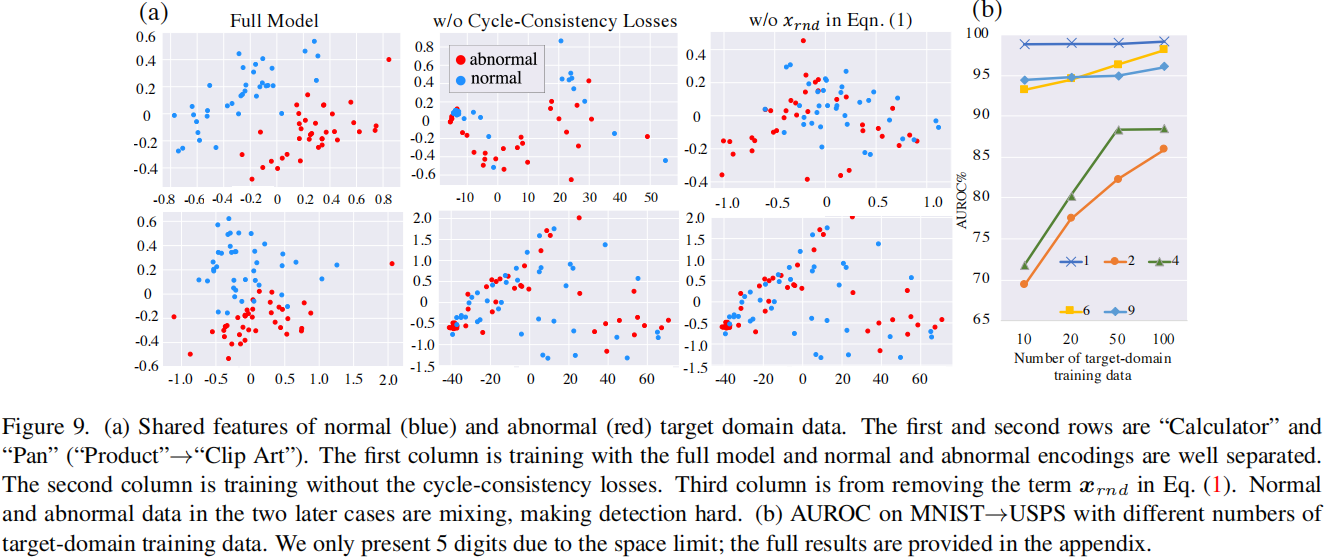
目标域训练数据数量的影响。 我们研究了IRAD性能与目标域训练数据数量\(n_t\)的关系。结果在图9(b)中展示了\(n_t=10,20,50,100\)。IRAD能够利用更多的目标数据实现更好的性能。