领域泛化+异常检测相关论文阅读整理

Anomaly Detection under Distribution Shift

ICCV 2023

用于异常检测的无监督方法。

训练集仅使用source distribution的normal数据。

测试集使用source 和 target distribution的数据，包含normal和anomaly。

认为在AD task中，训练数据通常只有一类。目前用于分类、检测和分割的OOD泛化方法需要考虑类标签、域标签或训练数据中样本的多样性[16,30,75,76]，这些方法通常不适用于AD任务。

方法：基于重构误差来进行异常检测。

在test的时候，使用 分布对齐 来将target distribution转换到source distribution

实验等具体细节可以点击这个链接

Domain Generalization via Feature Variation Decorrelation

ACMM 2021

domain generalization上的分类问题。有监督方法。知道source domain的样本、class label 和 domain label。

domain划分：一个是test domain，其余的都是source domain

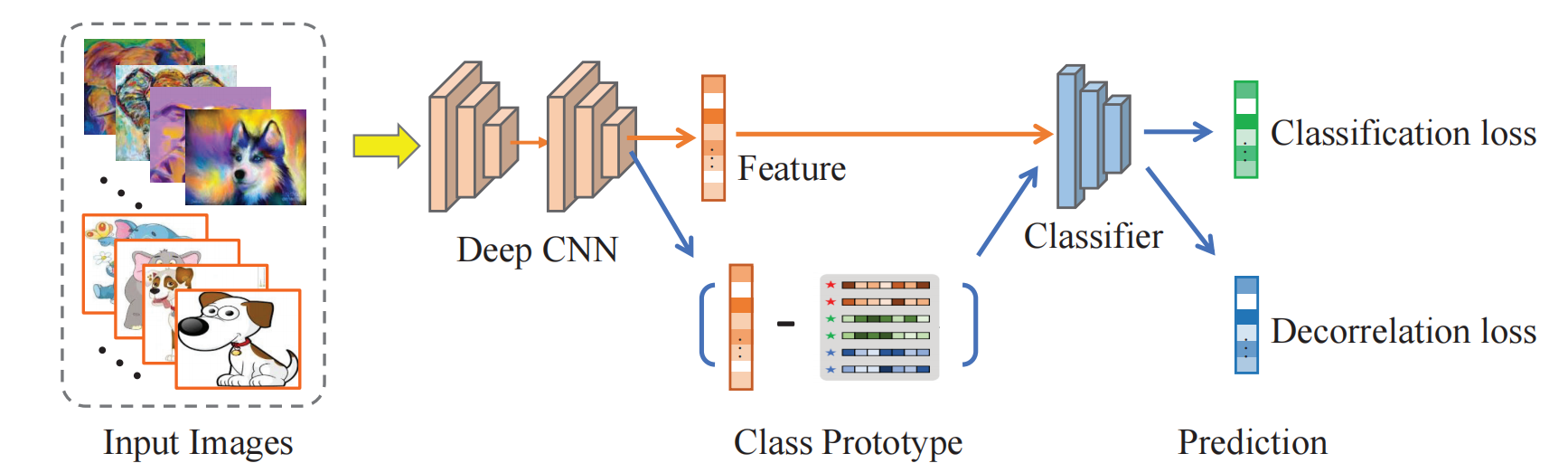
使用 \(F\) 提取特征，使用 \(C\) 进行分类。对于提取的特征 \(z\) ，基于已有的类别标签求出每个类的 class prototype \(\hat{\mu}_{y_j}\)。

\[\hat{\mu}_y=\frac{1}{K} \sum_{d=1}^K \hat{\mu}_y^d, \quad \hat{\mu}_y^d=\frac{1}{N_y^d} \sum_{j=1}^{N_y^d} z_j^i, \]

使用简单的线性减法，\(v_j=z_j-\hat{\mu}_{y_j}\) ，得到语义变量 \(v_j\)。

提出FVD loss，要求的 \(v_j\) 对于分类没有影响，简单来说是让分类器对于输入 \(v_j\) 的输出符合均匀分布。

\[\mathcal{L}_{F V D}=-\frac{1}{N} \sum_{j=1}^N C\left(\mathcal{F}\left(x_j\right)-\mu_{y_j}\right) \log \left(C\left(\mathcal{F}\left(x_j\right)-\mu_{y_j}\right)\right) . \tag{8} \]

然后使用下面这个损失函数，完成分类任务

\[\min _{\mathcal{F}, C} \frac{1}{N} \sum_{j=1}^N \mathcal{L}_{c e}\left(C\left(\mathcal{F}\left(x_j\right)\right), y_j\right), \tag{7} \]

最终loss为

\[\mathcal{L}_{\text {all }}=\mathcal{L}_{c e}-\lambda \mathcal{L}_{F V D}, \tag{9} \]

实验等具体细节可以点击这个链接

SelfReg: Self-supervised Contrastive Regularization for Domain Generalization

ICCV 2021

有监督方法。一个是test domain，其余的都是source domain。知道source domain的样本和 class label。

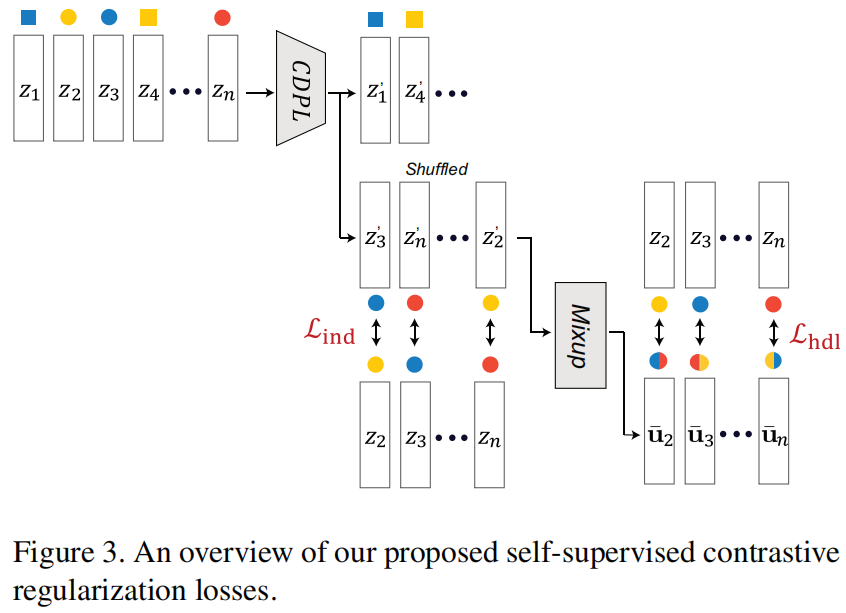
• 提出 Individualized In-batch Dissimilarity Loss：要求表征 \(z^c_i\) 与同一个batch中的都属于类别 \(c\) 的表征 \(z^c_j\) 靠近。其中 \(z^c_j\) 是随机选取的一个in-batch表征，并且 \(z_j^c\) 经过了一层MLP（称为CDPL）用于防止 representation collapse。

  \[\mathcal{L}_{\text {ind }}(\mathbf{z})=\frac{1}{N} \sum_{i=1}^N\left\|\mathbf{z}_i^c-f_{\mathrm{CDPL}}\left(\mathbf{z}_{j \in[1, N]}^c\right)\right\|_2^2 \tag{1} \]

• 提出 Heterogeneous In-batch Dissimilarity Loss ：对于经过CDPL的表征 \(u^c_i\)，从in-batch中选择一个表征 \(u_j^c\)，用two-domain Mixup获得一个插值表征 \(\bar{u}_i^c\)。然后通过损失函数，要求原来的表征 \(z_i^c\) 与 \(\bar{u}_i^c\) 靠近

  \[\overline{\mathbf{u}}_i^c=\gamma \mathbf{u}_i^c+(1-\gamma) \mathbf{u}_{j \in[1, N]}^c \tag{2} \]
  \[\mathcal{L}_{\text {hdl }}(\mathbf{z})=\frac{1}{N} \sum_{i=1}^N\left\|\mid \mathbf{z}_i^c-\overline{\mathbf{u}}_i^c\right\|_2^2 \tag{3} \]

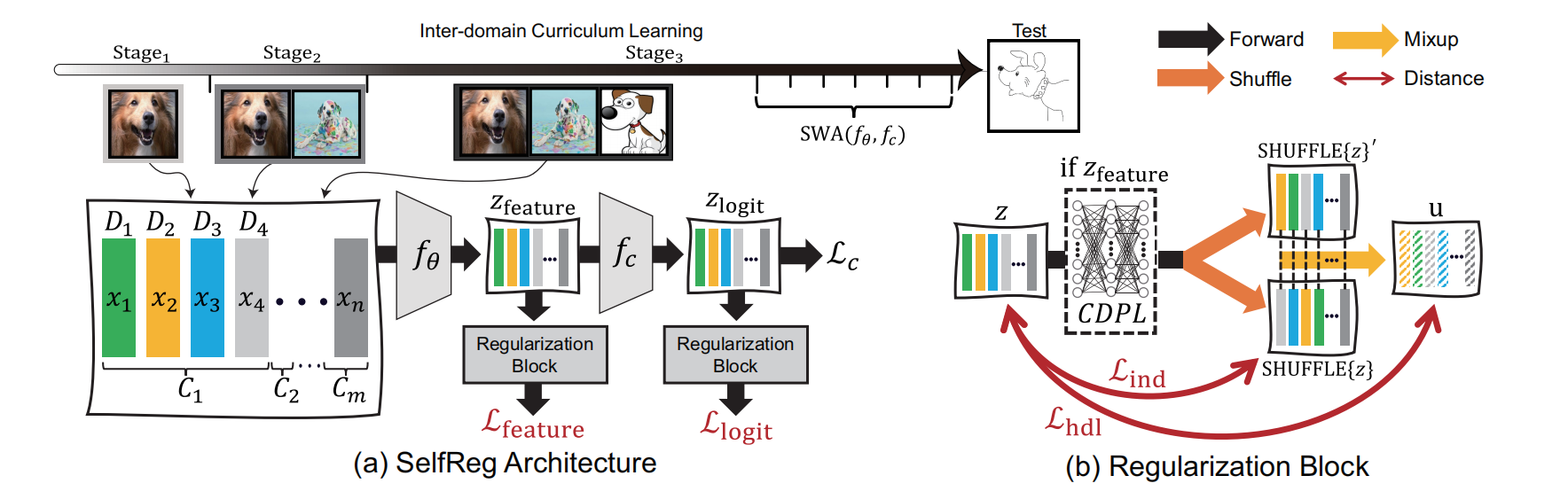
对 中间的表征层 和 最后的分类层 都应用上述两个individualized and heterogeneous inbatch dissimilarity losses，并且使用超参数控控制两层的平衡

\[\mathcal{L}_{\text {SelfReg }}=\lambda_{\text {feature }} \mathcal{L}_{\text {feature }}+\lambda_{\text {logit }} \mathcal{L}_{\text {logit }} \tag{4} \]

最终损失函数为

\[\mathcal{L}=\mathcal{L}_{\mathrm{c}}+\mathcal{L}_{\text {SelfReg }} \tag{5} \]

在初始训练阶段后，自监督对比损失 \(\mathcal{L}_{\text {SelfReg }}\) 变得主导，并引起了梯度不平衡，阻碍了适当的训练。

针对该问题

• 修改梯度大小以依赖于分类损失 \(\mathcal{L}_{\mathrm{c}}\) 的大小——即我们使用梯度大小修饰器 \(\min \left(1.0, \mathcal{L}_{\mathrm{c}}\right)\)，因此 \(\mathcal{L}_{\text {feature }}=\min \left(1.0, \mathcal{L}_{\mathrm{c}}\right)\left[\gamma \mathcal{L}_{\text {ind }}+(1-\gamma) \mathcal{L}_{\text {hdl }}\right]\)。

• 随机权重平均(Stochastic Weights Averaging ，SWA) ：对于模型权重空间 \(\Omega=\left\{\omega_0, \omega_1, \ldots, \omega_N\right\}\)，其中 \(N\) 是训练步骤的数量。以 \(c\) 作为周期长度，对于 SWA 的权重空间采样是 \(\Omega_{\text {swa }}=\left\{\omega_{m+k c}\right\}\)，其中 \(k \geq 0,0 \leq m \leq m+k c \leq N\)，

  \[\omega_{\text {swa }}=\frac{1}{k+1} \sum_{i=0}^k \omega_{m+i c} . \tag{6} \]

• Inter-domain Curriculum Learning (IDCL)：采用课程学习策略，其中源领域以有意义的顺序逐渐暴露，从而在训练过程中逐渐提供更复杂的领域。

实验等具体细节可以点击这个链接

Pcl: Proxy-based contrastive learning for domain generalization

CVPR 2022

直接应用基于对比的方法（例如，监督对比学习）在领域泛化中并不有效。认为由于不同领域之间存在显著的分布差异，对齐正样本对往往会妨碍模型的泛化。

在分类问题中，最后一般会使用softmax来输出分数向量，然后用Cross-Entropy Loss进行反向传播。关于对softmax+Cross-Entropy Loss求导的过程如下：https://zhuanlan.zhihu.com/p/37122897。由此得到损失函数中正分数和负分数的梯度可以表示为

\[\frac{\partial \mathcal{L}}{\partial s_i}= \begin{cases} p_i-1, & \text { 如果 } \mathrm{i} \text { 是正的; } \\ p_i, & \text { 如果 } \mathrm{i} \text { 是负的. } \end{cases} \tag{5} \]

根据方程（5），我们可以进一步推导出 \(\sum_{j \neq i} \frac{\partial \mathcal{L}}{\partial s_j}=\left|\frac{\partial \mathcal{L}}{\partial s_i}\right|\)，因为 \(\sum p_i=1\)，其中 \(i\) 表示正索引，\(j\) 表示负索引。这个方程表明，通过将正样本对拉近，负样本对被相同的力量推开。然后，负样本对的数量成为一把双刃剑。在contrastive-based loss中，每个正样本对必须将其他负样本对推开，这激发了正样本对获得更高的分数。在域泛化中，一些正样本对是由不同分布形成的，难以对齐，这可能影响模型的性能。

因此模型提出了基于代理的对比学习。使用目标类别代理来与样本形成正样本对。对于单个样本 \(x_i\)，仅在批内与负样本做相似度计算。

\[\mathcal{L}_{\mathrm{PCL}}=-\frac{1}{N} \sum_{i=1}^N \log \frac{\exp \left(\boldsymbol{w}_c^{\top} \boldsymbol{z}_i \cdot \alpha\right)}{Z} \tag{6} \]

\[Z=\exp \left(\boldsymbol{w}_c^{\top} \boldsymbol{z}_i \cdot \alpha\right)+\sum_{k=1}^{C-1} \exp \left(\boldsymbol{w}_k^{\top} \boldsymbol{z}_j \cdot \alpha\right)+\sum_{j=1, j \neq i}^K \exp \left(\boldsymbol{z}_i^{\top} \boldsymbol{z}_j \cdot \alpha\right) \]

这里 \(N\) 是一个小批量中的样本数，\(\boldsymbol{w}_c\) 表示 \(\boldsymbol{x}_i\) 的目标类别代理权重，\(C\) 是类别数，\(K\) 是所有 \(\boldsymbol{x}_i\)-基于样本对之间的负样本对数量。样本嵌入即 \(\boldsymbol{z}\) 和代理权重即 \(\boldsymbol{w}\) 都已标准化。\(\alpha\) 是缩放因子。

使用一个三层 MLP \(h(\cdot)\) 作为样本嵌入的投影头，以及一个单层 MLP \(g(\cdot)\) 作为代理权重的投影头，将代理权重和样本嵌入都映射到另一个空间。然后应用基于代理的对比损失，使代理权重和样本嵌入都可以学习更有意义的特征。新的嵌入和代理权重可以表示为 \(\boldsymbol{e}_i=h\left(\boldsymbol{z}_i\right)\) 和 \(\boldsymbol{v}_i=g\left(\boldsymbol{w}_i\right)\)。

将公式6的负样本范围从batch扩大到domain，并使用投影之后的嵌入做学习。

\[\mathcal{L}_{\mathrm{PCL}-\text{in}}=-\frac{1}{N} \sum_{i=1}^N \log \frac{\exp \left(\boldsymbol{v}_c^{\top} \boldsymbol{e}_i\right)}{E}, \tag{7} \]

\[E=\exp \left(\boldsymbol{v}_c^{\top} \boldsymbol{e}_i\right)+\sum_{k=1}^{C-1} \exp \left(\boldsymbol{v}_k^{\top} \boldsymbol{e}_j\right)+\sum_{j=1, j \neq i}^B \exp \left(\boldsymbol{e}_i^{\top} \boldsymbol{e}_j\right), \tag{8} \]

所有部分与前面的方程相同，只是考虑了在相同领域内的样本对的负样本。采取平衡的领域采样策略。在每个训练迭代中，我们从每个源领域中采样相同数量的样本，这意味着在每个小批次的训练迭代中\(N=\sum_{d=1}^D B_d\)

整体结构

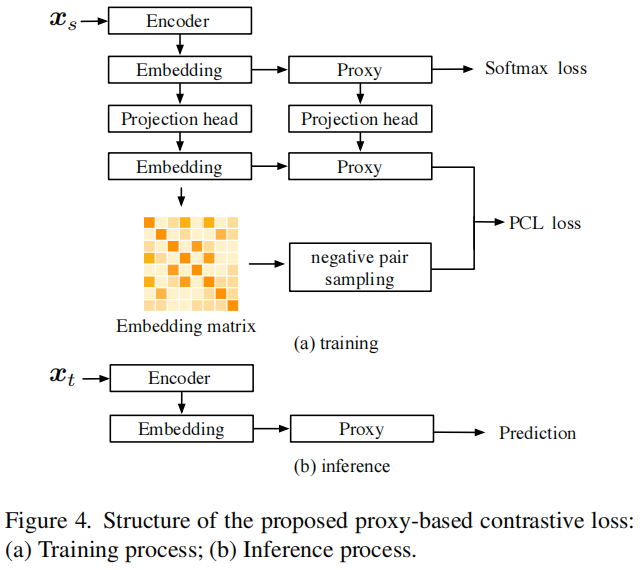
如图4所示。在训练阶段，我们为样本嵌入和代理权重分别对齐不同的投影头。然后，我们只从嵌入矩阵中选择负样本对来构建与代理权重相结合的基于代理的对比损失。最终的损失由以下方式给出：

\[\mathcal{L}_\text{final}=\mathcal{L}_\text{CE}+\lambda \cdot \mathcal{L}_\text{PCL-in} \tag{9} \]

其中，\(\mathcal{L}_\text{CE}\) 简单地是一个softmax CE损失。在推理阶段，我们只使用原始的样本嵌入和代理进行预测，而不引入额外的参数。

实验等具体细节可以点击这个链接

Mean-Shifted Contrastive Loss for Anomaly Detection

对比方法在视觉识别任务中取得了最先进的性能，但它们并不是为了OCC的特征适应而设计的。而且论文在使用ImageNet预训练特征优化OCC的对比损失时，表示不仅没有改进，而且迅速恶化。

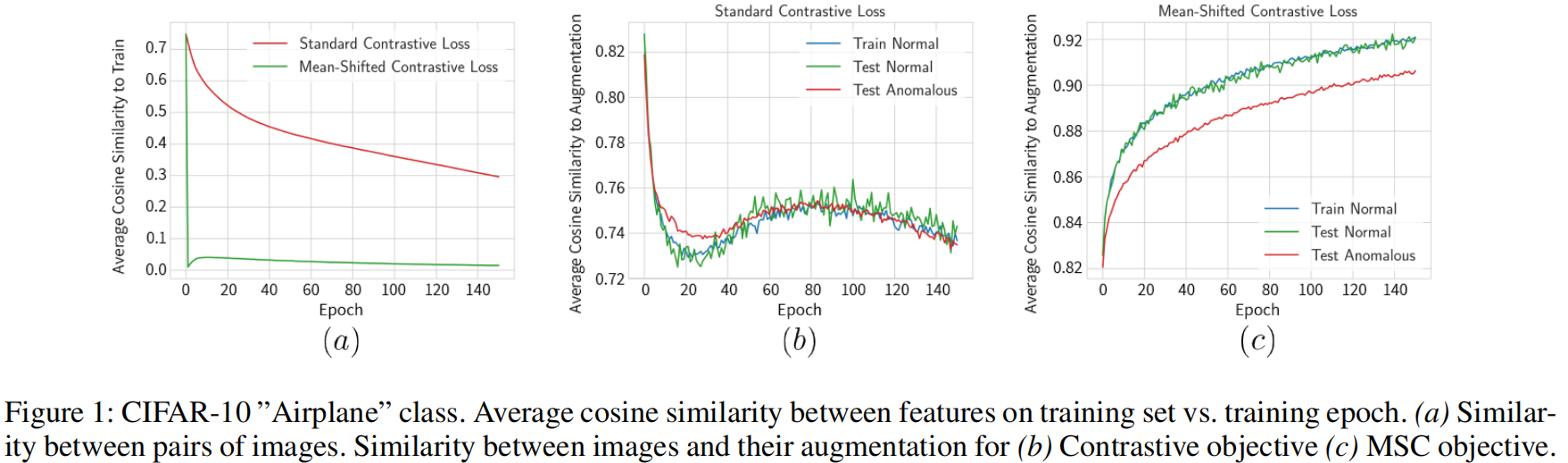
图1a表示训练集中示例对之间特征的余弦相似性的平均值，分布越均匀越接近零。

图1b，c表示，训练样本及其增强之间特征的余弦相似性的平均值。

（Wang和Isola，2020年）表明对比损失优化了两个属性：

1. 在单位球上均匀分布的 \(\{\phi(x)\}_{x\in\mathcal{X}_{train}}\) 。
2. 同一图像的不同增强映射到相同的表示。

论文表示：对比学习提高了分布的均匀性，但未能增加同一图像两个视图的特征之间的相似性。这表明对比学习并未使特征更具区分性。

论文提供了一个直观的解释。通常，正常数据在ImageNet预训练特征空间中占据一个紧凑的区域。当在以原点为中心的球坐标系中查看时，正常图像只跨越球的一个小的有界区域。由于对比学习的目标之一是使特征占据整个球，因此优化将集中在相应地更改特征上，对改善特征以使其对增强不变的重视要少得多。这对于异常检测来说是不利的，因为这种均匀性使得异常更难以检测（因为它们更不可能占据特征空间的稀疏区域）。此外，特征中的如此剧烈的变化会导致失去了预训练特征空间的有用属性。

为了解决上述问题，论文提出Mean-Shifted Contrastive Loss。

\(c\)表示训练集的标准化特征表示的中心：

\[c=\mathbb{E}_{x \in \mathcal{X}_{\text {train }}}\left[\frac{\phi_0(x)}{\left\|\phi_0(x)\right\|}\right] \tag{3} \]

通过从每个标准化特征表示中减去中心\(c\)来移动每个表示。来自大小为\(2B\)的增强mini-batch的某个图像\(x \in \mathcal{X}_{\text {train }}\)的两个增强\(\left(x_i, x_{i+B}\right)\)的MSC损失定义如下

\[\begin{aligned} & \mathcal{L}_{m s c}\left(x_i, x_{i+B}\right)=-\log ( \\ & \left.\frac{\exp \left(\operatorname{sim}\left(\frac{\phi\left(x_i\right)}{\left\|\phi\left(x_i\right)\right\|}-c, \frac{\phi\left(x_{i+B}\right)}{\left\|\phi\left(x_{i+B}\right)\right\|}-c\right) / \tau\right)}{\sum_{i=1}^{2 B} \mathbb{1}_{[i \neq m]} \cdot \exp \left(\operatorname{sim}\left(\frac{\phi\left(x_i\right)}{\left\|\phi\left(x_i\right)\right\|}-c, \frac{\phi\left(x_m\right)}{\left\|\phi\left(x_m\right)\right\|}-c\right) / \tau\right)}\right) \end{aligned} \tag{4} \]

其中\(\tau\)表示温度超参数，\(\operatorname{sim}\)是余弦相似性。

异常分数计算如下：

我们计算目标图像\(x\)的特征与\(k\)个示例\(N_k(x)\)之间的余弦相似性。可以通过\(k\)最近邻（更准确）或\(k\)均值（更快）来选择集合\(N_k(x)\)。

\[s(x)=\sum_{\phi(y) \in N_k(x)} 1-\operatorname{sim}(\phi(x), \phi(y)) \tag{5} \]

其中 \(sim\) 是余弦相似度。通过检查异常分数 \(s(x)\) 是否大于一个阈值，我们确定图像 \(x\) 是正常的还是异常的。

Standard Contrastive Loss 与 Mean-Shifted Contrastive Loss的比较

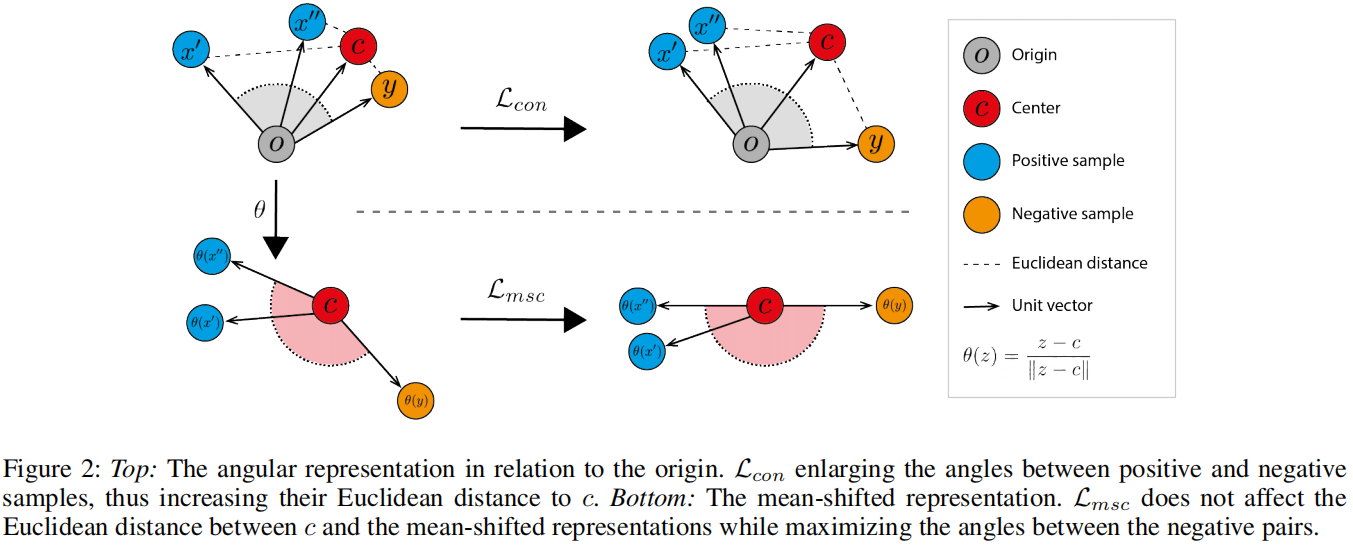
Standard Contrastive Loss即使在负对表示都是正常训练图像时也会最大化角度。通过最大化这些角度，与中心的距离也会增加，如图2（顶部）所示。\(y\) 是nomral，但是作为 x'的负样本出现。Standard Contrastive Loss让负样本对远离的同时，使其与center \(c\) 的距离增加。

这种行为与中心损失的优化方式（公式1）相反，中心损失通过最小化正常表示和中心之间的欧氏距离来学习表示。

Mean-Shifted Contrastive Loss不受此问题的困扰。与其测量样本与原点的角距离，论文测量样本与正常特征中心的角距离。如图2（底部）所示，Mean-Shifted Contrastive Loss最大化了负对之间的角度，同时保持了它们与中心的距离。

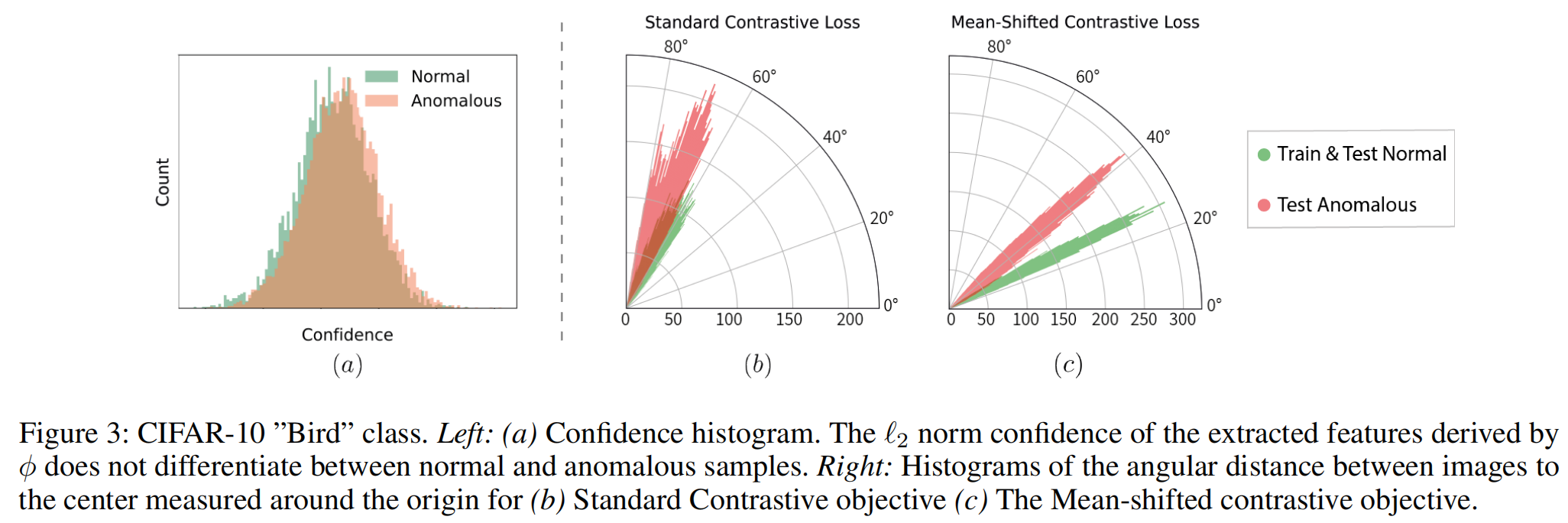
在图3.b-c 展示了图像到中心之间的角距离的直方图，其中（b）是Standard Contrastive Loss，（c）是Mean-Shifted Contrasrive Loss。在标准对比损失中，正常和异常特征的分布重叠，但在MSC损失中则不会。

实验等具体细节可以点击这个链接