[论文阅读] SelfReg: Self-supervised Contrastive Regularization for Domain Generalization

SelfReg: Self-supervised Contrastive Regularization for Domain Generalization

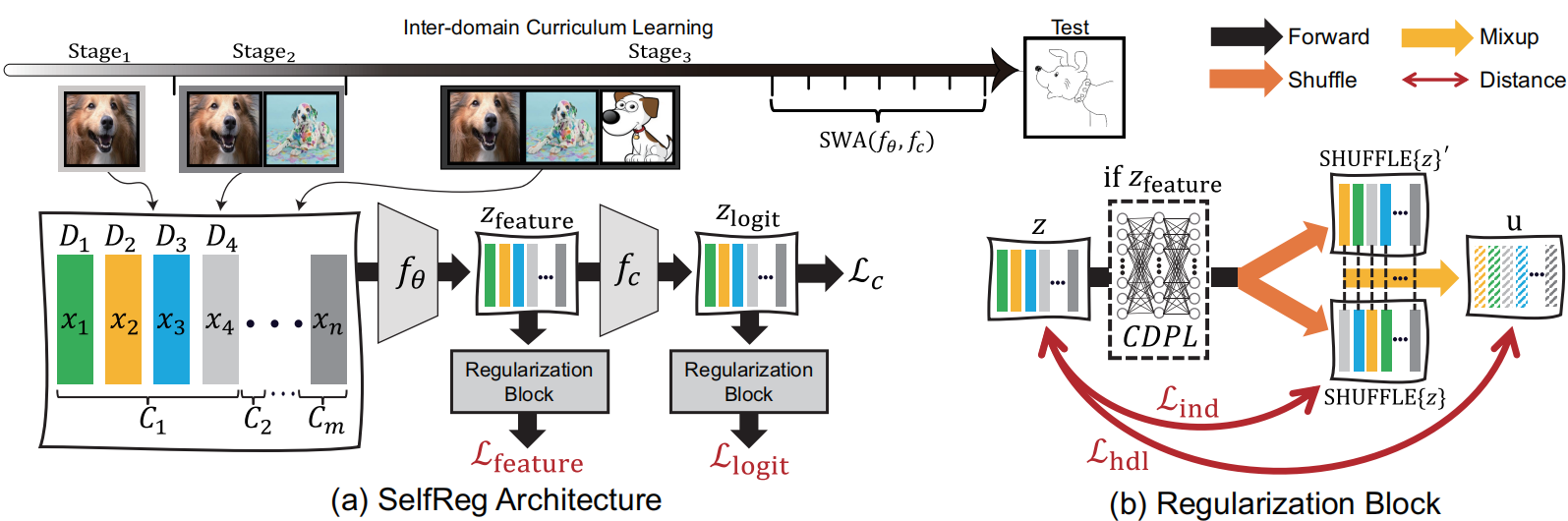
采用了自监督对比学习的方法，提出了Individualized In-batch Dissimilarity Loss和Heterogeneous In-batch Dissimilarity Loss。

Individualized In-batch Dissimilarity Loss 关注于在训练过程中对相同类别的样本进行比较。它利用了样本的潜在表示，并通过比较同一类别内部样本之间的差异来推动模型学习到更具区分性的特征。这种损失函数的设计使得模型更加关注于区分同一类别下的不同样本，有助于模型更好地区分不同类别之间的特征。

Heterogeneous In-batch Dissimilarity Loss 是针对在不同领域或不同条件下样本之间的差异进行建模的。它使用了在不同领域或条件下的潜在表示，并通过一种混合策略，即两个领域之间的混合操作，来生成插值的潜在表示。这种损失函数的目标是促使模型学习到在不同领域或条件下特征表示的一致性，从而提高模型对于领域变化的鲁棒性。

此外，模型还引入了一些训练策略，如随机权重平均（SWA），它利用多个局部最小值的模型参数快照的平均来寻找更平坦的损失最小值；以及跨领域课程学习（IDCL），它以有意义的顺序逐渐暴露源领域，以便在训练过程中逐步提供更复杂的示例。

3.1. Individualized In-batch Dissimilarity Loss

对于属于类标签 \(c \in \mathcal{C}\) 的潜在表示 \(\mathbf{z}_i^c=f_\theta\left(\mathbf{x}_i\right)\)， \(i \in \{1,2, \ldots, N\}\) ，我们计算个性化批内不相似损失 \(\mathcal{L}_{\text {ind }}\)。请注意，我们使用由参数 \(\theta\) 参数化的特征生成器 \(f_\theta\)，并且使用批大小 \(N\)。"相同类别"潜在表示的正对之间的不相似度如下公式1所示：

\[\mathcal{L}_{\text {ind }}(\mathbf{z})=\frac{1}{N} \sum_{i=1}^N\left\|\mathbf{z}_i^c-f_{\mathrm{CDPL}}\left(\mathbf{z}_{j \in[1, N]}^c\right)\right\|_2^2 \tag{1} \]

其中 \(\mathbf{z}_j^c\) 是从具有相同类别标签 \(c \in \mathcal{C}\) 的其他批内潜在表示 \(\left\{\mathbf{z}_i^c\right\}\) 中随机选择的。请注意，我们只考虑同时优化正对的对齐性和表示分布的均匀性。正如[17]中讨论的那样，我们使用额外的 MLP 层 \(f_{\mathrm{CDPL}}\)，称为特定类别的领域扰动层，以防止所谓的表示坍塌造成的性能下降。我们在第4.4节提供了消融研究以确认使用 \(f_{\mathrm{CDPL}}\) 能够获得更好的性能。

为了提高计算效率，我们使用以下两个步骤来找到所有的正对。（i）我们首先将潜在表示 \(\mathbf{z}_i\) 进行聚类和排序成相同类别组，即对于 \(c \in \mathcal{C}\)，得到 \(\left\{\mathbf{z}_i^c\right\}\)。（ii）对于每个相同类别组，我们通过随机洗牌修改其顺序，并获得 \(\operatorname{SHUFFLE}\left\{\mathbf{z}_i^c\right\}\)。（iii）最后，我们从 \(\left\{\mathbf{z}_i^c\right\}\) 和 \(\operatorname{SHUFFLE}\left\{\mathbf{z}_i^c\right\}\) 按顺序形成一个正对。

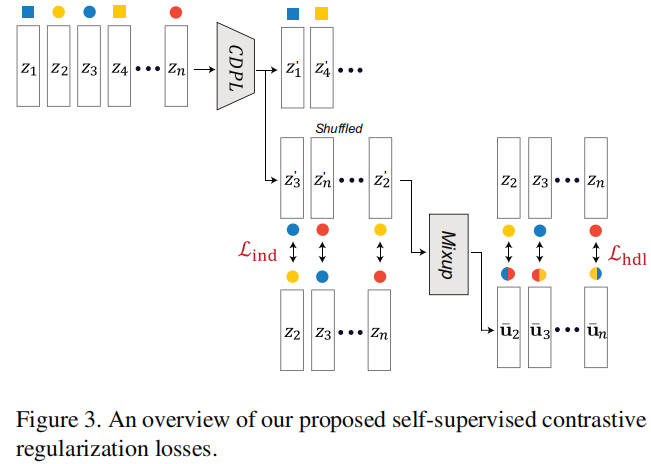
3.2. Heterogeneous In-batch Dissimilarity Loss

为了进一步推动模型学习领域不变表示，我们使用了一种额外的损失，称为异构批内不相似损失。在前一步得到的潜在表示 \(\mathbf{u}_i=f_{\mathrm{CDPL}}\left(\mathbf{z}_i^c\right)\) 的基础上，我们应用了一个双领域混合层，以获得跨不同领域的插值潜在表示 \(\overline{\mathbf{z}}_i\)。这将使模型在混合分布上正则化 [46]，即来自不同领域样本的凸组合。这与Wang等人提出的一层相似，其定义如下：

\[\overline{\mathbf{u}}_i^c=\gamma \mathbf{u}_i^c+(1-\gamma) \mathbf{u}_{j \in[1, N]}^c \tag{2} \]

其中 \(\gamma \sim \operatorname{Beta}(\alpha, \beta)\)，对于 \(\alpha=\beta \in(0, \infty)\)。类似地，\(\mathbf{u}_j^c\) 是从具有相同类别标签的 \(\left\{\mathbf{u}_i^c\right\}\) 中随机选择的，对于 \(i \in\{1,2, \ldots, N\}\)。请注意，\(\gamma \in[0,1]\) 由超参数 \(\alpha\) 和 \(\beta\) 控制。

最后，我们计算异构批内不相似损失 \(\mathcal{L}_{\text {hdl }}(\mathbf{z})\) 如下：

\[\mathcal{L}_{\text {hdl }}(\mathbf{z})=\frac{1}{N} \sum_{i=1}^N\left\|\mid \mathbf{z}_i^c-\overline{\mathbf{u}}_i^c\right\|_2^2 \tag{3} \]

3.3. Feature and Logit-level Self-supervised Contrastive Losses

所提出的个性化和异构批内不相似损失可以应用于中间特征和分类器的logits。我们使用损失函数 \(\mathcal{L}_{\text {SelfReg }}\) 如下所示：

\[\mathcal{L}_{\text {SelfReg }}=\lambda_{\text {feature }} \mathcal{L}_{\text {feature }}+\lambda_{\text {logit }} \mathcal{L}_{\text {logit }} \tag{4} \]

其中，我们使用 \(\lambda_{\text {feature }}\) 和 \(\lambda_{\text {logit }}\) 控制每个项的强度。由于我们使用损失函数的线性形式，通常需要适当平衡网络参数，以生成既用于原始分类任务又具有领域不变性的特征。我们观察到，在初始训练阶段后，我们的自监督对比损失 \(\mathcal{L}_{\text {SelfReg }}\) 变得主导，并引起了梯度不平衡，阻碍了适当的训练。为了缓解这个问题，我们应用了两种梯度稳定技术：（i）损失剪裁和（ii）随机权重平均（SWA），以及（iii）跨领域课程学习（IDCL）。对于（i），我们修改梯度大小以依赖于分类损失 \(\mathcal{L}_{\mathrm{c}}\) 的大小——即我们使用梯度大小修饰器 \(\min \left(1.0, \mathcal{L}_{\mathrm{c}}\right)\)，因此 \(\mathcal{L}_{\text {feature }}=\min \left(1.0, \mathcal{L}_{\mathrm{c}}\right)\left[\gamma \mathcal{L}_{\text {ind }}+(1-\gamma) \mathcal{L}_{\text {hdl }}\right]\)。这个技术在训练期间动态平衡这些损失是有效的。对于（ii）和（iii），我们分别在第3.4节和第3.5节中讨论了详细内容。

最终损失函数最终我们使用以下损失函数 \(\mathcal{L}\)，包括分类损失 \(\mathcal{L}_{\mathrm{c}}\) 和我们的自监督对比损失 \(\mathcal{L}_{\text {SellReg }}\)：

\[\mathcal{L}=\mathcal{L}_{\mathrm{c}}+\mathcal{L}_{\text {SelfReg }} \tag{5} \]

3.4. Stochastic Weights Averaging (SWA)

随机权重平均（SWA）是一种集成技术，通过对训练过程中多个局部最小值导出的模型参数快照进行平均，以找到损失空间中更平坦的最小值 [23]。已知找到更平坦的最小值能够保证更好的泛化性能 [19]，因此它已经被用于需要高泛化性能的领域自适应和泛化领域 \([48,6]\)。

给定模型权重空间 \(\Omega=\left\{\omega_0, \omega_1, \ldots, \omega_N\right\}\)，其中 \(N\) 是训练步骤的数量。对于采样模型权重并没有特定的约束，但通常在模型充分收敛时的特定周期内进行采样。我们使用 \(c\) 作为周期长度，并且对于 SWA 的权重空间采样是 \(\Omega_{\text {swa }}=\left\{\omega_{m+k c}\right\}\)，其中 \(k \geq 0,0 \leq m \leq m+k c \leq N\)，这里的 \(m\) 表示 SWA 的初始步骤。然后我们可以推导出平均权重 \(w_{\text {swa }}\) 如下所示：

\[\omega_{\text {swa }}=\frac{1}{k+1} \sum_{i=0}^k \omega_{m+i c} . \tag{6} \]

3.5. Inter-domain Curriculum Learning (IDCL)

在领域泛化文献中，利用ImageNet预训练的ConvNet作为骨干网络是一种常见做法。然后，这样的模型通常会通过随机展示来自所有源领域 \(\mathcal{D}_i\)（\(i \in\{1,2, \ldots, M\}\)）的示例进行微调，这往往会使训练变得不稳定，因为它会优化冲突方向上的梯度。

在这里，我们采用课程学习策略，其中源领域以有意义的顺序逐渐暴露，从而在训练过程中逐渐提供更复杂的领域。我们首先根据与骨干网络预训练的领域（例如ImageNet [9]数据集）的距离对 \(M\) 个源领域进行排序，得到有序的源领域 \(\mathcal{D}_i^{\prime}\)（\(i \in 1,2, \ldots, M\)）。我们将整个训练过程划分为 \(M\) 个子阶段 \(s \in\{1,2, \ldots, M\}\)。在每个阶段 \(s\)，模型只暴露于源领域的子集，即 \(\left\{\mathcal{D}_{i \leq s}^{\prime}\right\}\) - 模型逐渐学习更复杂的示例。

我们观察到，基于这种课程学习的训练策略提供了显著的性能改进，可能是由于对冲突梯度的正则化。我们在第4.4节提供了详细信息。