[论文阅读] Mean-Shifted Contrastive Loss for Anomaly Detection

Mean-Shifted Contrastive Loss for Anomaly Detection

Abstract

这篇文章探讨了异常检测领域的一个关键问题，即如何通过使用预训练特征来提高异常检测性能。研究者首先介绍了异常检测的背景和现有方法，指出了使用自监督学习和外部数据集预训练特征的潜力。然后，他们详细分析了标准对比损失在使用ImageNet预训练特征时的适用性问题，发现标准对比损失无法有效地利用这些预训练特征进行异常检测。接着，研究者提出了一种新的损失函数，即均值平移对比损失（MSC），以克服标准对比损失的限制。他们解释了MSC损失如何改进特征的一致性和紧凑性，从而提高了异常检测性能。最后，研究者进行了大量实验证明他们的方法在多个数据集上实现了最新的异常检测性能。文章的主要贡献在于提出了一种新的损失函数，可以更好地适应预训练特征，从而改进了异常检测的效果。

contributions

1. 我们分析了用于OCC的微调预训练表示的标准对比损失，并展示它初始化不良并且性能不佳。

2. 提出了一种替代目标，即 Mean-Shifted Contrastive Loss，并分析了它在异常检测特征适应中的重要性。

3. 进行了广泛的实验，展示了我们的方法在异常检测性能方面的最新成果（例如，在CIFAR-10上达到了98.6%的ROC-AUC）。

3 Background: Learning Representations for One-Class Classification

3.1 初步

在一类分类任务中，我们得到了一组全部为正常（不包含异常）的训练样本 \(x_1, x_2 \ldots x_N \in \mathcal{X}_{\text {train }}\)。目标是将新样本 \(x\) 分类为正常或异常。这里考虑的方法是学习一个由神经网络函数 \(\phi: \mathcal{X} \rightarrow \mathbb{R}^d\) 参数化的样本的深度表示，其中 \(d \in \mathbb{N}\) 是特征维度。在一些方法中，\(\phi\) 是由预训练权重 \(\phi_0\) 初始化的，可以通过使用外部数据集（例如ImageNet分类）或使用训练集上的自监督任务进行学习。表示进一步在训练数据上进行调整，形成最终的表示 \(\phi\)。最后，异常评分函数 \(s(\phi(x))\) 确定样本 \(x\) 的异常分数。通过在 \(s(x)\) 上应用阈值，可以预测二元异常分类。在第3.2和第3.3节中，我们将回顾学习表示 \(\phi\) 的最相关的方法。

3.2 Self-supervised Objectives for OCC

Center Loss:

该损失使用一个简单的思想，即特征应该被学习，以便正常数据位于特征空间的一个紧凑区域内，而异常数据位于外部。由于我们专注于OCC设置，训练中没有异常示例。相反，中心损失鼓励正常样本的特征尽可能地靠近预定的中心。具体来说，对于输入样本 \(x \in \mathcal{X}_{\text {train }}\)，中心损失可以表示如下：

\[\mathcal{L}_{\text {center }}(x)=\|\phi(x)-c\|^2 \tag{1} \]

这个目标存在一个平凡的解决方案 - 特征 \(\phi(x)\) 对于所有样本，包括正常和异常样本，都会坍缩到一个奇异点 \(c\)。这通常被称为"灾难性崩溃"。这样的坍缩表示当然无法区分正常和异常样本。

Contrastive Loss:

最近，对比学习在自监督表示学习中取得了很多进展（Chen et al. 2020）。在对比训练过程中，随机抽取了一个大小为 \(B\) 的小批量，并在从小批量中导出的增强示例对上定义了对比预测任务，从而产生了 \(2 B\) 个数据点。对于OCC，对比目标简单地规定：

（i）任何正样本对 \(\left(x_i, x_{i+B}\right)\) 的特征之间的角距离应该很小

（ii）正常样本 \(x_i, x_m \in \mathcal{X}_{\text {train }}\) 的特征之间的距离，其中 \(i \neq m\)，应该很大。正样本对 \(\left(x_i, x_{i+B}\right)\) 的典型对比损失如下所示，其中 \(x_i\) 和 \(x_{i+B}\) 是某个 \(x \in \mathcal{X}_{\text {train }}\) 的增强：

\[\mathcal{L}_{\text {con }}\left(x_i, x_{i+B}\right)=-\log \frac{\exp \left(\operatorname{sim}\left(\phi\left(x_i\right), \phi\left(x_{i+B}\right)\right) / \tau\right)}{\sum_{m=1}^{2 B} \mathbb{1}[i \neq m] \cdot \exp \left(\operatorname{sim}\left(\phi\left(x_i\right), \phi\left(x_m\right)\right) / \tau\right)} \]

其中，对于所有的 \(m \in [1,2 B]\)，\(x_m\) 是某个 \(x \in \mathcal{X}_{\text {train }}\) 的增强视图，\(\tau\) 表示温度超参数，sim 表示余弦相似度。目前，对比方法在没有使用外部训练网络权重的情况下实现了OCC的最佳性能。

4 Modifying the Contrastive Loss for Anomaly Detection

4.1 Adaptation Failure of The Contrastive Loss

尽管对比方法在视觉识别任务中取得了最先进的性能，但它们并不是为了OCC的特征适应而设计的。在这里，我们报告并分析一个令人惊讶的结果：在使用ImageNet预训练特征优化OCC的对比损失时，表示不仅没有改进，而且迅速恶化。

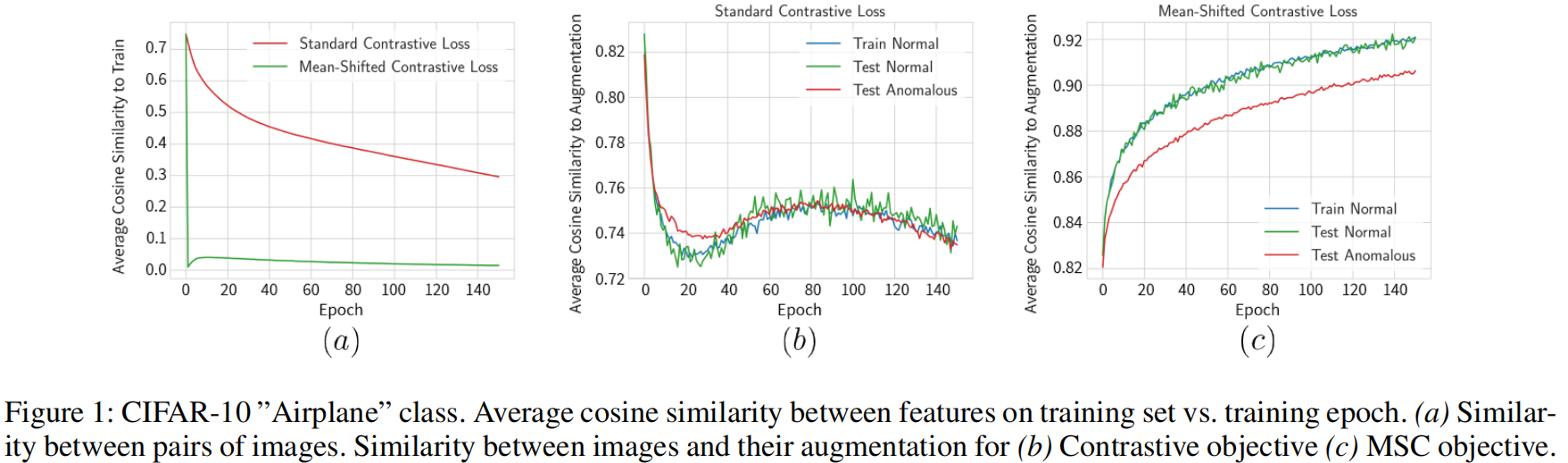
为了理解这一现象，我们在图1中呈现了两个指标随着训练时期的变化情况：

1. uniformity：训练集中示例对之间特征的余弦相似性的平均值（更均匀=接近零）
2. augmentation distance：训练样本及其增强之间特征的余弦相似性的平均值（更高通常表示特征空间的更好排序）。

（Wang和Isola，2020年）表明对比损失优化了两个属性：

1. 在单位球上均匀分布的 \(\{\phi(x)\}_{x\in\mathcal{X}_{train}}\) 。
2. 同一图像的不同增强映射到相同的表示。

我们可以看到，对比训练提高了分布的均匀性，但未能增加同一图像两个视图的特征之间的相似性。这表明对比训练并未使特征更具区分性，这暗示了训练目标未得到很好的规定。

我们为这一经验观察提供了一个直观的解释。通常，正常数据在ImageNet预训练特征空间中占据一个紧凑的区域。当在以原点为中心的球坐标系中查看时，正常图像只跨越球的一个小的有界区域。由于对比学习的目标之一是使特征占据整个球，因此优化将集中在相应地更改特征上，对改善特征以使其对增强不变的重视要少得多。这对于异常检测来说是不利的，因为这种均匀性使得异常更难以检测（因为它们更不可能占据特征空间的稀疏区域）。此外，特征中的如此剧烈的变化会导致失去了预训练特征空间的有用属性。这与传输强大的辅助特征的目标相悖。

4.2 The Mean-Shifted Contrastive Loss for Better Adaptation

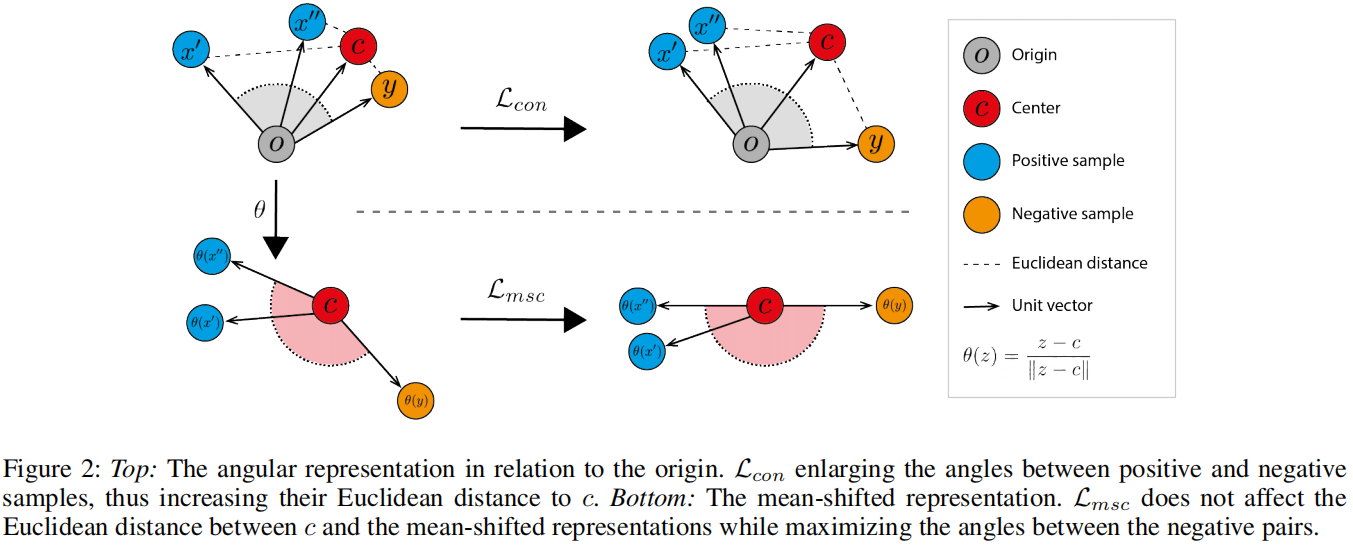
为了克服上述所述的对比学习的限制，我们提出了一种简单的目标函数修改，用于适应OCC特征。在我们修改后的目标函数中，我们计算图像特征相对于正常特征中心的角度，而不是原始对比损失中所做的相对于原点的计算。尽管这可以看作是原始目标的简单转换，但我们将展示它解决了上述提到的关键问题，并允许对比学习受益于强大的预训练特征初始化（详见第4.3节）。我们将这个新目标称为 Mean-Shifted Contrastive.（MSC）。

让我们用\(c\)表示训练集的标准化特征表示的中心：

\[c=\mathbb{E}_{x \in \mathcal{X}_{\text {train }}}\left[\frac{\phi_0(x)}{\left\|\phi_0(x)\right\|}\right] \tag{3} \]

其中\(\phi_0\)是初始化的预训练模型。对于每个图像\(x\)，我们创建图像的两种不同增强，记为\(x_i, x_{i+B}\)。首先，所有增强图像都通过特征提取器 \(\phi\) 传递。然后，它们通过\(\ell_2\) 标准化缩放到单位球面上（有关使用\(\ell_2\)标准化的动机，请参见第5.2节）。我们通过从每个标准化特征表示中减去中心\(c\)来均值位移每个表示。来自大小为\(2B\)的增强mini-batch的某个图像\(x \in \mathcal{X}_{\text {train }}\)的两个增强\(\left(x_i, x_{i+B}\right)\)的MSC损失定义如下：

\[\begin{aligned} & \mathcal{L}_{m s c}\left(x_i, x_{i+B}\right)=-\log ( \\ & \left.\frac{\exp \left(\operatorname{sim}\left(\frac{\phi\left(x_i\right)}{\left\|\phi\left(x_i\right)\right\|}-c, \frac{\phi\left(x_{i+B}\right)}{\left\|\phi\left(x_{i+B}\right)\right\|}-c\right) / \tau\right)}{\sum_{i=1}^{2 B} \mathbb{1}_{[i \neq m]} \cdot \exp \left(\operatorname{sim}\left(\frac{\phi\left(x_i\right)}{\left\|\phi\left(x_i\right)\right\|}-c, \frac{\phi\left(x_m\right)}{\left\|\phi\left(x_m\right)\right\|}-c\right) / \tau\right)}\right) \end{aligned} \tag{4} \]

其中\(\tau\)表示温度超参数，\(\operatorname{sim}\)是余弦相似性。

Anomaly criterion

为了将样本分类为正常或异常，我们使用与一组\(K\)个适当选择的训练样本示例\(N_k(x)\)的余弦相似性。可以通过\(k\)最近邻（更准确）或\(k\)均值（更快）来选择集合\(N_k(x)\)。我们计算目标图像\(x\)的特征与\(k\)个示例\(N_k(x)\)之间的余弦相似性。异常分数由以下公式给出：

\[s(x)=\sum_{\phi(y) \in N_k(x)} 1-\operatorname{sim}(\phi(x), \phi(y)) \tag{5} \]

其中 \(sim\) 是余弦相似度。通过检查异常分数 \(s(x)\) 是否大于一个阈值，我们确定图像 \(x\) 是正常的还是异常的。

4.3 Understanding the Mean-Shifted Loss

Uniformity：

使用标准对比损失优化预训练权重会侧重于优化以原点为中心的球体周围的均匀性，但会损害特征的语义相似性（请参见第4.1节）。MSC损失提出了一个简单但非常有效的解决方案——在围绕数据中心的坐标框架中评估均匀性。由于这个框架中的特征已经大致归一化，优化过程会侧重于提高它们的语义相似性。如图1所示，从初始化开始，我们的目标使特征保持均匀性（正常示例之间的余弦相似性较低）。因此，优化可以集中于改进特征。

Compactness around center:

标准对比损失即使在负对表示都是正常训练图像时也会最大化角度。通过最大化这些角度，与中心的距离也会增加，如图2（顶部）所示。这种行为与中心损失的优化方式（公式1）相反，中心损失通过最小化正常表示和中心之间的欧氏距离来学习表示。 Reiss等人（2021）表明，优化中心损失会导致高的异常检测性能。我们提出的损失不受此问题的困扰。与其测量样本与原点的角距离，我们测量样本与正常特征中心的角距离。如图2（底部）所示，我们提出的损失最大化了负对之间的角度，同时保持了它们与中心的距离。

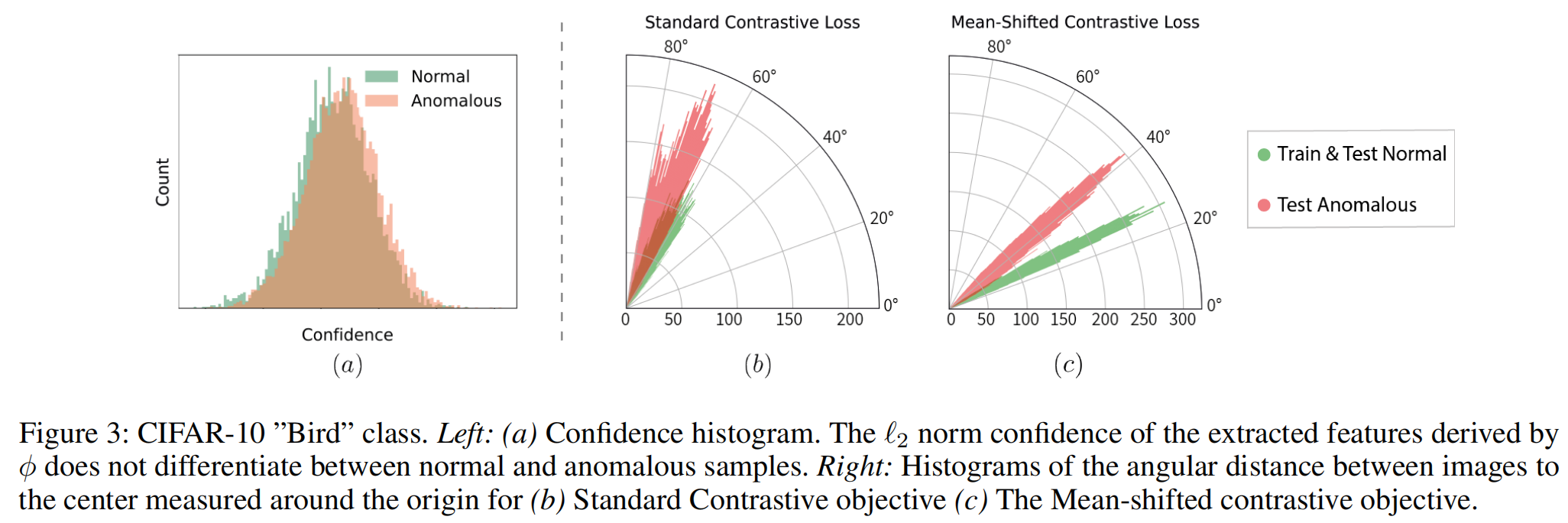
在图3.b-c中，我们展示了图像到中心之间的角距离的直方图，其中（i）是标准对比损失，（ii）是我们的MSC损失。在标准对比损失中，正常和异常特征的分布重叠，但在我们的MSC损失中则不会。

5 Experiments

5.1 Main Results

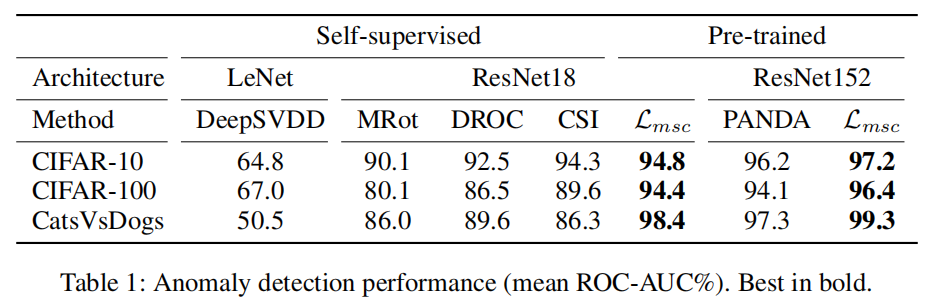
根据标准协议，通过将一个类设置为正常，将所有其他类设置为异常，将多类数据集转换为异常检测。表1显示，我们提出的方法在common OCC benchmarks 上超过了以前的最先进的方法。

5.2 Further Analysis & Ablation Study

Small datasets

我们可以看到，自监督方法在这样小的数据集上表现不佳，而我们的方法取得了非常强大的性能。

自监督方法在小数据集上表现不佳的原因在于它们只能使用如此小的样本量进行训练，无法学习强大的特征。这对于对比方法来说尤其严重（但对于所有其他自监督方法也是如此）。而预训练方法可以从外部数据集转移特征，因此表现更好。

The Angular Representation.

初始特征提取器\(\phi_0\)是在分类任务（ImageNet分类）上进行预训练的。我们提出将表示\(\phi_0\)分解为两个组成部分：(i) 语义类别\(\frac{\phi_0(x)}{|\phi_0(x)|}\)，以及(ii) 置信度\(\| \phi_0(x) \|\)。

置信度确定类别间区分的置信度。我们进行了彻底的调查，发现ImageNet预训练特征表示的置信度对异常检测性能没有帮助。在图3.a中，我们比较了CIFAR-10数据集的一个特定类别上正常和异常值之间置信度值的直方图。我们观察到，在该数据集中，置信度不能区分正常和异常图像。在图4中，我们展示了 mean-shifted representation对类别置信度的敏感性。这强调了MSC优化中置信度归一化的重要性。

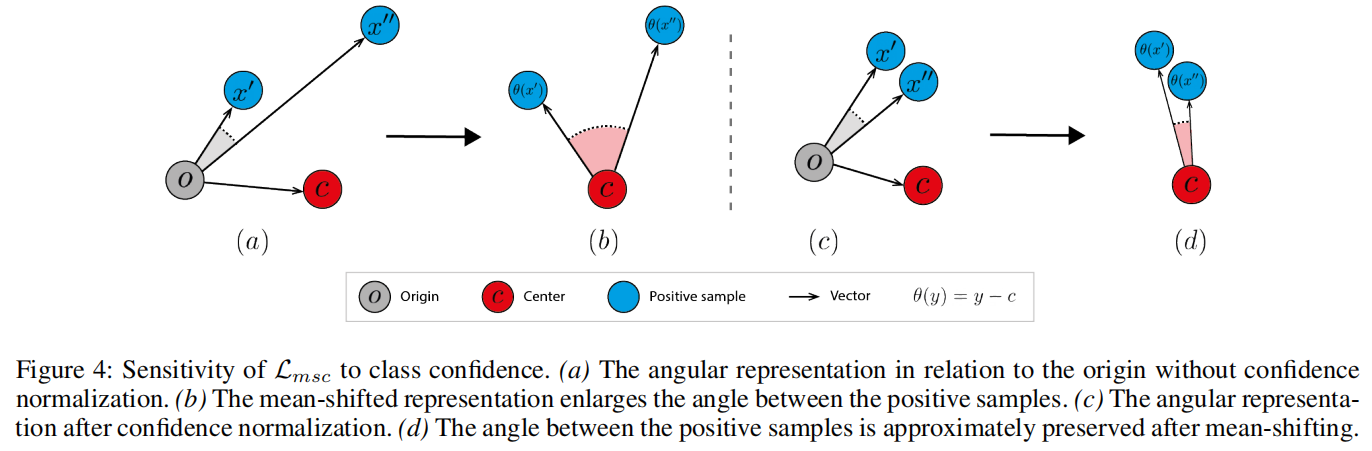
因此，我们提出使用角中心损失。角中心损失鼓励每个样本与中心之间的角距离最小。这与标准中心损失（由PANDA和DeepSVDD使用）使用欧几里德距离的方法相反。尽管只是一个简单的更改，角中心损失比常规中心损失获得了更好的结果（见表3）。

\[\mathcal{L}_{ang}=-\phi(x)\cdot c \tag{6} \]

Training objective.

在表3中，对消融实验进行了呈现。请注意，DN2和PANDA的置信度不变形式均优于它们的欧氏版本。我们进一步注意到，MSC损失表现优于其他损失，并将其与角中心损失相结合可以进一步改进。

Optimization from scratch.

Mean-Shifted目标假设特征相对于中心的距离与高检测性能相关。当将中心初始化为随机的高斯向量时，我们失去了这一强有力的先验，因此检测能力大大降低。因此，当从头开始训练模型，没有来自预训练模型的强初始化时，我们的损失函数不会优于标准对比损失。因此，MSC损失是对预训练特征的异常检测的直接贡献。

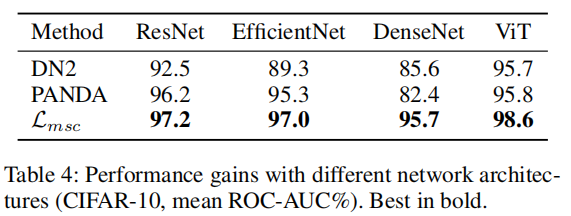
Performance on different network architectures.

在表4中，我们提供了DN2、PANDA和我们的方法在ImageNet预训练的主要CNN和ViT架构上的CIFAR-10 ROC-AUC％结果。PANDA对架构的选择敏感，对ViT没有改进，并在DenseNet上崩溃。我们的MSC损失可以跨架构推广，导致显著的性能提升，包括CIFAR-10上的98.6% ROC-AUC。

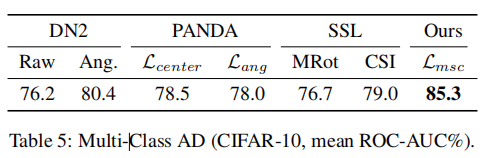
Multi-Class Anomaly Detection.

我们评估了（Ahmed和Courville，2020年）引入的多类别异常检测设置，其中正常数据包含多个语义类别。请注意，正常数据没有提供类别标签。这个设置比单类别设置更具挑战性，因为正常数据具有多模式分布。对于每个实验，我们将CIFAR-10的一个类别标记为异常，其他CIFAR-10类别标记为正常。我们在表5中报告了10个实验的平均ROC-AUC％。PANDA对于DN2（具有余弦距离）没有改进，因为数据不再是单模态的，因此不是紧凑的。相反，我们的MSC损失不同程度上不依赖于单模态假设，并产生比以前的预训练和自监督方法更好的结果。

Detection scoring functions.

kNN具有良好建立的近似方法，可以减少其推断时间复杂性。一个简单但有效的解决方案是通过k均值减少普通样本集合。在表6中，我们比较了我们的方法及其特征的k均值近似在正常训练图像的特征被压缩成不同