[论文阅读] Unsupervised Anomaly Detection by Robust Densit

参考资料：

1. 《Unsupervised Anomaly Detection by Robust Density Estimation》
2. 维基百科-利普希茨连续
3. 非凸优化基石：Lipschitz Condition
4. 详细解析深度学习中的 Lipschitz 条件
5. 谱归一化（Spectral Normalization）的理解

Unsupervised Anomaly Detection by Robust Density Estimation

Introduction

与GAN，VAE相比，flow-based模型显示地学习密度函数，这使其成为推断分布外数据的有力工具。

由于深度神经网络的高容量，flow-based模型估计的密度函数可能被异常破坏。因此，需要一种更鲁棒的方法来估计密度函数，以提高基于流的模型在无监督AD任务中的性能。

本文提出了RobustRealNVP，它在学习密度函数时忽略了低密度点，使用Lipschitz正则化来增强估计密度函数的*滑性。

贡献点：

• 提出了一种鲁棒的flow-based的深度密度估计方法用于无监督异常检测。
• 我们提出理论分析来证明它对污染训练数据的鲁棒性。具体地说，我们证明了它收敛到在干净(无异常)数据上训练的Real NVP的 \(\epsilon\) *似*稳点。
• 我们进行了大量的实验，以表明我们的框架优于各种最先进的方法。

Preliminaries

给定 \(n\) 个样本 \(\{x_i \in \mathbb{R}^d\}_{i=1}^n\) ，flow-based模型旨在通过最大化观测数据的似然函数 \(\max_\theta\ p_\theta(X)\) 来学习从简单分布(如高斯分布)到更复杂目标分布的可逆映射，其中 \(\theta\) 为网络参数。

关于Real NVP的知识可以参考原论文 《Density estimation using real nvp》 和 博客

这里给出一个后续会提到的公式。

\[y_{1:d}=x_{1:d}\\ y_{d+1:D}=x_{d+1:D} \odot exp[s(x_{1:d})]+t(x_{1:d}) \tag{1} \]

Methodology

我们的目标是开发一种鲁棒的flow-based的无监督AD方法，适用于可能包含异常的训练数据。在此设置中，我们的目标函数为:

\[-\min\sum_{x\in \mathcal{N \cup A}}{\log (p_Z(f(x))) + \log\left( \left| \det \left( \frac{\partial f(x)}{\partial x} \right) \right| \right)} \tag{2} \]

其中 \(\mathcal A\) 是异常的集合。直接优化(2)可能会因为异常的不利影响导致结果不佳。

Robustness for Density Estimation

设 \(\epsilon \in [0,0.5]\) 为异常比，即训练数据中出现异常的比例。给定来自密度函数 \(p\) 的一组正常实例 \(\mathcal N\) 和来自任意密度函数的一组异常实例 \(\mathcal A\) ，我们的目标是学习 \(\Psi:\mathcal{N \cup A} \rightarrow \hat{p}\) ，使得 \(\mathcal N\) 的负对数似然的梯度范数最小。 \(\hat{p}\) 用 \(\theta\) 参数化表示，则学习目标为:

\[\min_\theta \left \| -\sum_{x\in\mathcal{N}} \nabla_\theta \log \hat{p}_\theta(x) \right \| \]

优化目标函数具有挑战性，因为我们不知道哪个实例属于 \(\mathcal N\)或 \(\mathcal A\)。我们提出了一种鲁棒梯度估计方法来解决这个问题。考虑最小化负对数似然函数的梯度下降方法。给定一个数据点 \(x_i\)，它对应的梯度为

\[g_i=-\nabla_\theta \log \hat{p}_\theta(x_i)=-\frac{1}{\hat{p}_\theta(x_i)}\frac{\partial \hat{p}(x_i)}{\partial \theta} \]

给定 \(n\) 个数据点，令 \(\mathbf{G}=[g_1^T,g_2^T,\dots,g_n^T]\in\mathbb{R}^{n \times d}\) 为带污染的梯度矩阵，\(\Gamma:\mathbb{R}^{n \times d} \rightarrow \mathbb{R}^d\) 为聚合函数。可以使用梯度下降法更新模型参数，如下所示

\[\theta^{(t+1)}=\theta^{(t)}-\eta^{(t)}\Gamma(\mathbf{G}) \]

如果 \(\Gamma(\cdot)\) 为经验均值，则更新公式简化为标准梯度下降。但是，由于 \(\mathbf{G}\) 中同时包含了正常数据和异常数据的梯度，因此不能保证 \(\Gamma(\mathbf{G})\) 与干净数据的梯度接*。因此，我们的目标是设计一个鲁棒函数 \(\Gamma\)，优化以下目标，以确保估计的密度不会被异常破坏

\[\min_\Gamma\| \Gamma(\mathbf{G}) -\mu \|^2 \]

其中 \(\mu = \frac{1}{\mathcal{N}}\sum_{i\in\mathcal{N}}g_i\) 为干净数据的梯度

问题是：如果存在一个常数 \(\zeta\) ，使得在每个梯度下降步骤中梯度差的上界都是 \(\zeta\) ，即 \(\forall t: \| \Gamma(G)^t-\mu^{(t)} \|^2 \leq \zeta\)，我们能保证驻点有一个有界的梯度范数吗？

下面的命题给出了有界梯度范数收敛时的这样一个保证。

Proposition 1 (Convergence of Biased SGD)

设 \(\phi\) 为目标函数，\(\theta\) 为待优化变量。在mild Lipschitz 假设下，\(\zeta\) 表示干净的mini-batch梯度 \(\mu\) 和带污染的 mini-batch 梯度之间的差的最大 \(l_2\) 范数 ，即\(\Gamma(G):\| \mu - \Gamma(G) \| \leq \zeta\)。通过使用偏梯度估计 \(\Gamma(G)\)， SGD收敛于 \(\zeta\) 逼*的*稳点：\(\mathbb{E}(|\nabla_\phi(\theta_t)|) = \mathbb{O}(\zeta)\)

为了完整起见，我们在这里包含上述命题，以表明设计一种鲁棒均值估计方法足以保证最终解在其干净(无异常)目标方面具有小的梯度范数。

Robust Gradient Method for Density Estimation

我们对 \(\Gamma(G)\) 的鲁棒聚合函数的工作原理如下。给定大小为 \(m\) 的小批 \(\mathcal{B}\)，我们对 \(\mathcal{B}\) 中每个实例的损失进行排序，并丢弃损失最大的前 \(k\) 个实例。我们将证明该策略确保了算法的鲁棒性保证。在讨论细节之前，我们首先介绍下面的Lipschitz假设。

Assumption 1 ： DNN学习到的密度函数 \(\hat{p}(x)\) ，关于它的参数 \(\theta\)，\(\forall \theta_1,\theta_2,x:\| \hat{p}_{\theta_1}(x) -\hat{p}_{\theta_2}(x) \| \leq \hat{L} \| \theta_1 - \theta_2 \|\)

上述假设保证了梯度范数的上界为 \(\hat{L}\)

通过在 \(\hat p\) 上应用 \(\hat{L}\)-smooth 假设，我们可以对单个梯度范数进行如下的约束

\[\| g_i \|=\| -\nabla_\theta \log \hat{p}_\theta(x_i) \|=\frac{1}{\hat{p}_\theta(x_i)}\left\| \frac{\partial \hat{p}_\theta(x_i)}{\partial \theta} \right\| \leq \frac{\hat{L}}{\hat{p}_\theta(x_i)} \]

由于损失 \(-\log \hat{p}_\theta(x)\) 随着 \(\frac{1}{\hat{p}_\theta(x)}\) 的增加而单调减小，因此，在每次迭代中，我们的算法只需要对每个数据点的当前估计密度 \(\hat{p}_{\theta^{(t)}}(x)\) 进行排序，并丢弃密度低的数据点。然后从剩余的数据点计算*均梯度 \(\hat{\mu}^{(t)}\)，用于执行梯度下降更新：\(\theta^{(t+1)}=\theta^{(t)}-\eta^{(t)}\hat{\mu}^{(t)}\) 。算法1中给出的伪代码总结了这一点。

我们将首先使用以下引理来证明算法1具有鲁棒性保证

Lemma 1 (Mean Gradient Estimation Error)

设 \(g_i^{(t)}\) 为第 \(i\) 个数据在第 \(t\) 次迭代时的梯度，\(\mathcal N\) 为干净的数据，而 \(\hat{\mu}^{(t)}\) 为算法1在第 \(t\) 次迭代时的输出。对于梯度估计误差有如下保证:

\[\left\| \frac{1}{|\mathcal{N}|}\sum_\mathcal{N}{g_i^{(t)}-\hat{\mu}^{(t)}} \right\|^2=\mathbb{O}(\epsilon)\hat{L} \]

假设 \(|g|_{i\in\mathcal{N}} \leq \frac{1}{\hat{p}_i}\hat{L}\)， \(\max_{i\in\mathcal{N}}\frac{1}{\hat{p}_i}=C\)。

我们的方法是估计剩余的梯度向量的经验均值，这些梯度向量大小有限（即小于 \(C\hat{L}\)）。

当 \(\hat L\) 较小时，由于剩余梯度（可能包括异常）的大小有限，因此每个剩余异常对*均梯度估计的影响也有限，不超过 \(C\hat{L}\) 。在最坏的情况下，如果没有异常被丢弃，这将引入 \(\mathbb{O}(\epsilon)\) 的异常。把它们放在一起，我们得到上述错误率 \(\mathbb{O}(\epsilon)\hat{L}\) ，其中 \(C\) 是常数被忽略。

由上述引理可知，当 \(\epsilon\) 较小时，梯度估计误差由Lipschitz常数控制。结合命题1，如果我们可以控制Lipschitz常数很小(即具有光滑的损失面)，那么训练数据中异常的存在不会显著改变干净数据的密度估计。

前面的分析表明，要使梯度估计具有鲁棒性，必须满足以下两个假设。

• \(\hat{p}_{i \in \mathcal{N}}\)必须足够大，以保证 \(C\) 很小。这是一个合理的假设，因为数据包含的大多是正常的观测值。
• 预测的密度函数应足够*滑，以避免异常的不良影响。如果异常是稀疏的，即没有聚类，那么将它们包含在训练数据中对估计密度的影响很小，因为异常的密度很小。然而，聚类异常由于其相对较高的密度，会使密度估计产生偏差。为了避免这种聚集异常的影响，我们提出了一种谱归一化方法来*滑学习到的密度。

Spectral Normalization

谱归一化(SN)方法(Miyato et al. 2018)的动机是以下不等式 \(\|g_1 \circ g_2\|_{\text{Lip}} \leq \| g_1 \|_{\text{Lip}} \cdot \| g_2 \|_{\text{Lip}}\) ，其中 \(\cdot\) 表示Lipschitz常数。神经网络可以看作是一系列线性变换函数和激活函数的组合。由于大多数激活函数是Lipschitz连续的（例如，RELU函数的Lipschitz常数为1），如果每个线性层的Lipschitz常数是有界的，那么整个网络的Lipschitz常数也是有界的。

对于一个线性函数 \(\phi:h \rightarrow Wh\) ，其中 \(W\) 是一个线性变换矩阵，其Lipschitz常数的上界是矩阵 \(W\) 的算子范数，即 \(\|W\|_{op}\) 。因此，整个网络的Lispchitz函数的上界是 \(\prod_{i=1}^v\|W_i\|_{op}\) ，其中 \(v\) 为层数(对于RELU网络)。

在SN的原文中，每一层归一化如下: \(W_{SN}=\frac{W}{\|W\|_{op}}\)，以保证函数是1-Lipschitz。然而，1-Lipschitz可能会使函数过于*滑，导致密度函数的欠拟合。在这项工作中，我们提出了以下SN来满足k- lipschitz约束 \(W_SN=\frac{W}{\|W\|_{op}/k}\)。

Lipschitz Regularization for Flow-based Model

SN假设DNN可以分解为一系列线性变换和激活函数。然而，对于基于流的模型，网络不再是线性变换和激活函数的简单分解。虽然可以用SN来保证式(1)中学习到的函数 \(s\) 和 \(t\) 是 k-smoothness的，但目前还没有任何证据证明整个变换是 k-smoothness 的。在本节中，我们证明约束 \(s\) 和 \(t\) 足以实现 k-smoothness。我们的基本原理是基于谱归一化的以下两个引理：

Lemma 2

如果 \(f:\mathbb{R}^n \rightarrow \mathbb{R}^n\) 是处处可微的函数，其雅可比矩阵 \(J\) ，\(\|J\|_{op} \leq L\) 当且仅当 \(f\) 是 \(L\)-smooth 的。

Lemma 3

\(\|[\mathbf{A}, \mathbf{B}]\|_{o p} \leq\|\mathbf{A}\|_{o p}+\|\mathbf{B}\|_{o p}\), 其中 \([\cdot, \cdot]\) 表示矩阵拼接

式(1)中变换的雅可比矩阵如下:

\[\mathbf{J}=\frac{\partial y}{\partial x^T}=\left[\begin{array}{cc} \mathbb{I}_d & 0 \\ \frac{\partial y_{d+1: D}}{\partial x_{1: d}^T} & \operatorname{diag}\left(\exp \left[s\left(x_{1: d}\right)\right]\right) \end{array}\right] . \]

矩阵可以进一步分解为一个对角矩阵和一个非对角矩阵的和。因此

\[\begin{aligned} |\mathbf{J}|_{o p} & \leq\left|\left[\begin{array}{cc} \mathbb{I}_d & 0 \\ 0 & \operatorname{diag}\left(\exp \left[s\left(x_{1: d}\right)\right]\right) \end{array}\right]\right|_{o p}+\left|\left[\begin{array}{cc} 0 & 0 \\ \frac{\partial y_{d+1: D}}{\partial x_{1: d}^T} & 0 \end{array}\right]\right|_{o p} \\ & =\max \left(1, \max _{i \in[1,2, \ldots, D-d]} \exp \left[s\left(x_{1: d}\right)\right]_i\right)+\left|\frac{\partial y_{d+1: D}}{\partial x_{1: d}^T}\right|_{o p} . \end{aligned} \]

注意，如果函数 \(s\) 的输出是有界的，则第一项是有界的。在我们的实验中，我们使用tanh函数作为函数s的最后一层。因此，第一项将以 \(\exp(1)\) 为界。对于第二项，根据式(1)，我们有

\[\begin{aligned} & \left|x_{d+1: D} \odot \exp \left(s\left(x_{1: d}\right)\right)+t\left(x_{1: d}\right)\right|_{\text {Lip }} \\ & \quad \leq\left|x_{d+1: D} \odot \exp \left(s\left(x_{1: d}\right)\right)\right|_{\text {Lip }}+\left|t\left(x_{1: d}\right)\right|_{\text {Lip }} . \end{aligned} \]

Since \(s\) and \(t\) are bounded by a Lipschitz constant using \(\mathrm{SN}\), assuming \(\|x\|\) is bounded by \(B\) and the last layer of \(s\) is a tanh function, then, according to the inequality \(\left\|g_1 \circ g_2\right\|_{\text {Lip }} \leq\left\|g_1\right\|_{\text {Lip }} \cdot\left\|g_2\right\|_{\text {Lip }}\), it is easy to see that the transformation \(y_{d+1: D}=x_{d+1: D} \odot \exp \left(s\left(x_{1: d}\right)\right)+t\left(x_{1: d}\right)\) has a bounded Lipschitz constant \(B * \exp (1) *|s|_{\text {Lip }}+|t|_{\text {Lip }}\). Thus the operator norm \(\left|\frac{\partial y_{d+1: D}}{\partial x_{1: d}^T}\right|_{o p}\) is also bounded. Finally, by Lemma 2, we conclude that application of SN to the functions \(s\) and \(t\) will guarantee that the flow model is Lipschitz regularized, which in turn, guarantees that the learned density function are not affected by clustered anomalies.

Anomaly Detection from Trained Network

通过在训练过程中丢弃低估计密度的数据点，并在基于流的模型中加入谱归一化，可以训练出鲁棒的密度估计函数。在测试过程中，可以通过应用训练好的网络来推断每个测试点的密度。每个测试点的异常分数由其估计密度给出，密度越高异常分数越低。

Experimental Evaluation

Experiments on Synthetic Data

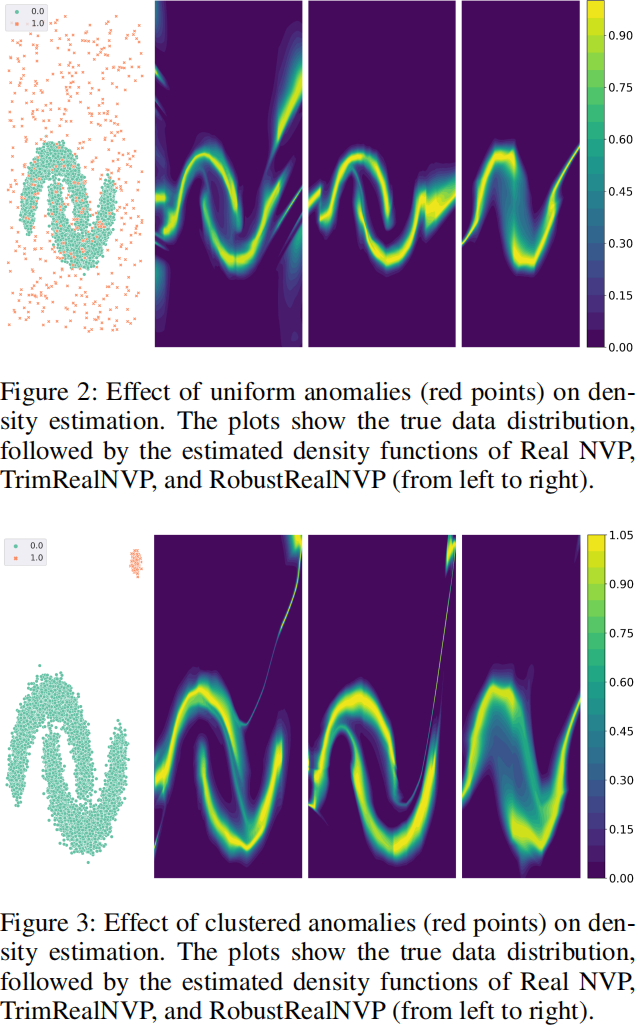
引理1表明，估计密度函数的鲁棒性受到预测函数*滑度的影响，而*滑度取决于异常分布。如果异常分布均匀，则不需要进行谱归一化处理。但是，如果异常是聚类的，则需要SN来提供鲁棒性保证。

我们将我们的算法RobustRealNVP与RealNVP的性能进行了比较。我们还研究了一种没有通过SN进行Lipschitz正则化的框架变体，并将这种方法称为TrimRealNVP。

实验结果如图3所示。TrimRealNVP虽然成功地缓解了均匀异常的影响，但受聚类异常的影响很大。Real NVP的估计密度函数也受到这两种异常的影响。RobustRealNVP可以有效地处理这两种类型的异常，因为它使用SN来增加损失图的*滑度，这反过来又使梯度估计更加鲁棒。

Experiments on Real-World Data

Datasets

• Stony Brook ODDS library (Rayana 2016), which contains 16 benchmark outlier detection data.
• CIFAR10, which is an image dataset with high-dimensional features.

我们首先在ImageNet上应用预训练的VGG19网络，并使用其最后一层之前的输出作为提取的特征。然后，我们应用PCA将其维数从4096降至128。

Baseline Methods

We compare RobustRealNVP against the following baseline methods:

1. AE (autoencoder) and VAE (variational autoencoder).
2. Deep-SVDD (Ruff et al. 2018), a deep 1-class SVM method.
3. SO-GAAL (Liu et al. 2019), a GAN-based anomaly detection approach.
4. OCSVM (Chen, Zhou, and Huang 2001), a shallow 1- class SVM method.
5. LOF (Breunig et al. 2000), a local density-based AD method.
6. IF (Liu, Ting, and Zhou 2008) (isolation forest), an ensemble tree-based method.

Experiment Settings

对于ODDS数据集，我们使用60%的数据用于训练，40%的数据用于测试。

对于CIFAR10数据集，保留80%的数据用于训练，剩下的20%用于测试。CIFAR10包含来自10个类的图像。我们选择一个类作为正常类(有5000个样本)，然后通过两种方式从其余类中创建异常：

• 从其他类中随机采样异常。
• 从一个特定类别中选择异常。设置训练异常率为0.1。

所有模型都在一个*衡的CIFAR10测试集上进行评估，每个类包含1000个样本。所有实验用5种不同的随机种子重复。

对于无监督AD，超参数调优比较棘手，因为没有清晰的验证数据可用。相反，我们固定了所有方法的网络结构，以确保公*比较。使用的超参数的详细信息在附录中给出。

结果报告使用AUC分数作为我们的评估指标。

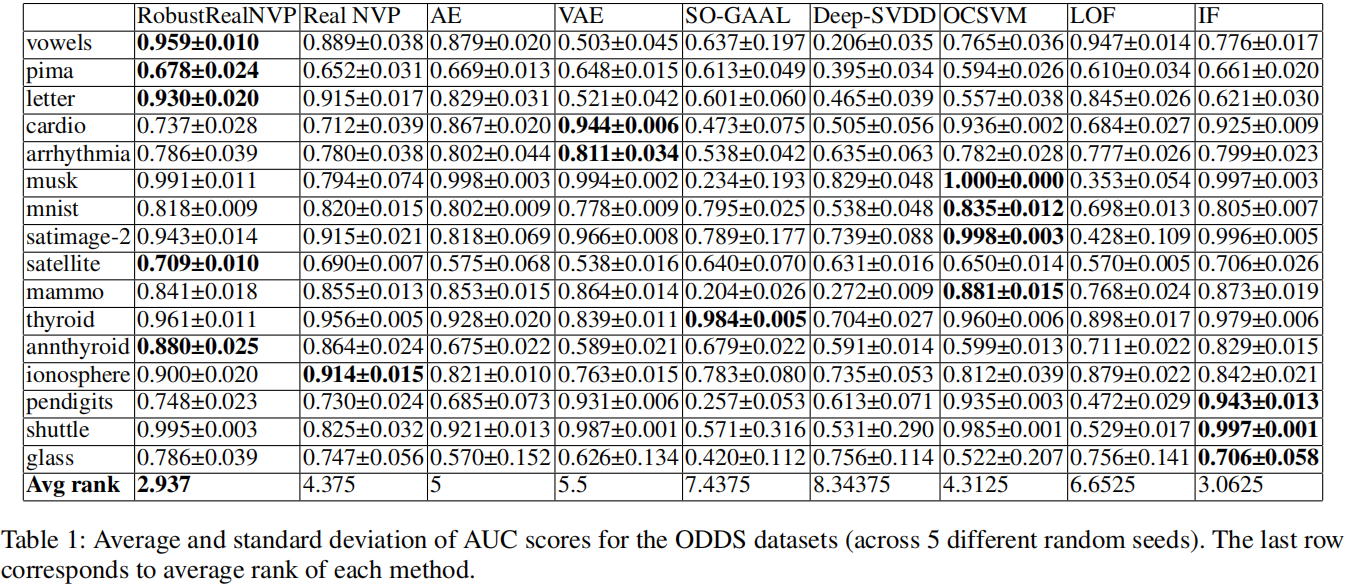
Results for ODDS data

表1显示了ODDS数据集上各种方法的AUC分数。考虑到数据集的多样性，没有一种方法能始终优于所有其他方法，但与其他基线相比，RobustRealNVP的*均排名最高。IF也达到了高度竞争的结果。深度学习方法(即SO-GAAL, Deep-SVDD)产生的结果相对较差，因为它们中的大多数是为干净的训练数据设计的，这在无监督的AD设置中是不可用的。

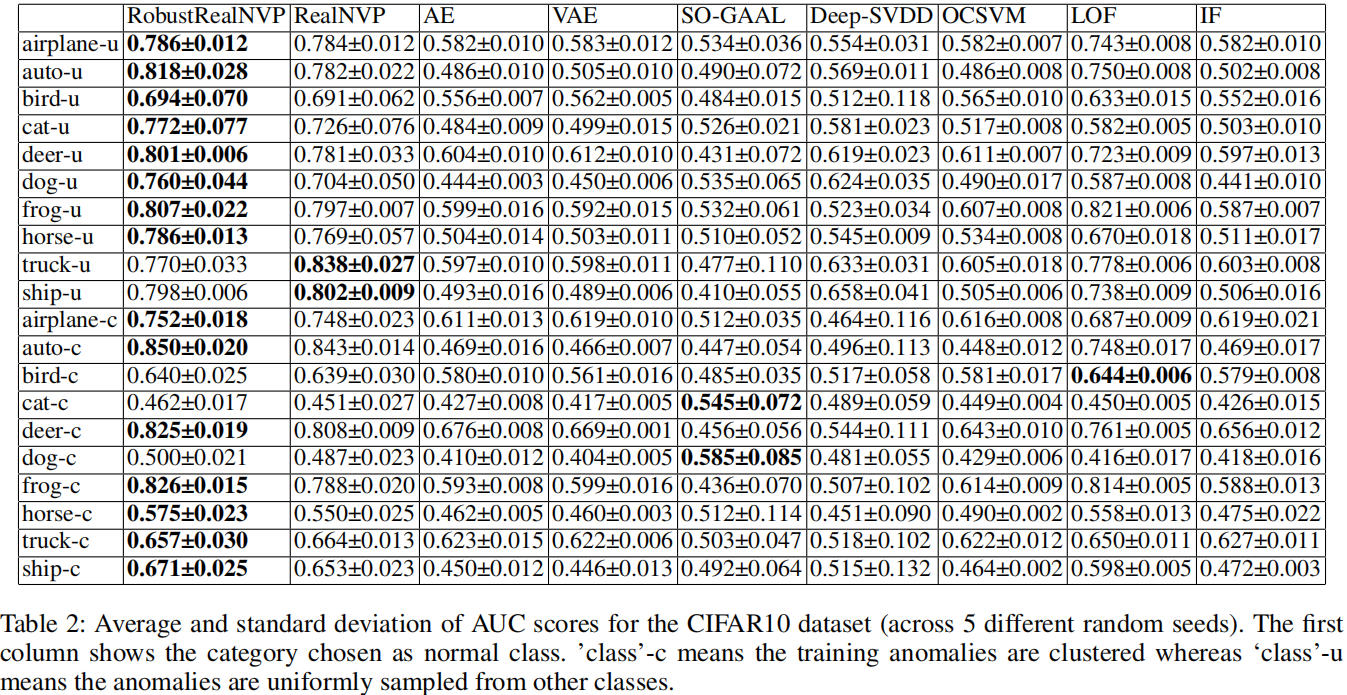
Results for CIFAR10

表2给出了选择不同类别的图像作为正常类时，各种方法的AUC得分。

在20个实验中的15个中，RobustRealNVP优于所有基线方法。与ODDS结果类似，深度学习方法在受污染的数据上训练时表现不佳。对于Deep-SVDD，表2中报告的AUC分数略低于原始论文(Ruff et al. 2018)中报告的值，因为我们的实验是在受污染的训练数据上进行的，而不是干净的训练数据。然而，即使我们使用Deep-SVDD论文中报告的结果(使用干净的训练数据)，RobustRealNVP在所有10个具有均匀异常的CIFAR10数据集上仍然优于Deep-SVDD。此外，Deep-SVDD在异常集中的数据上也表现不佳

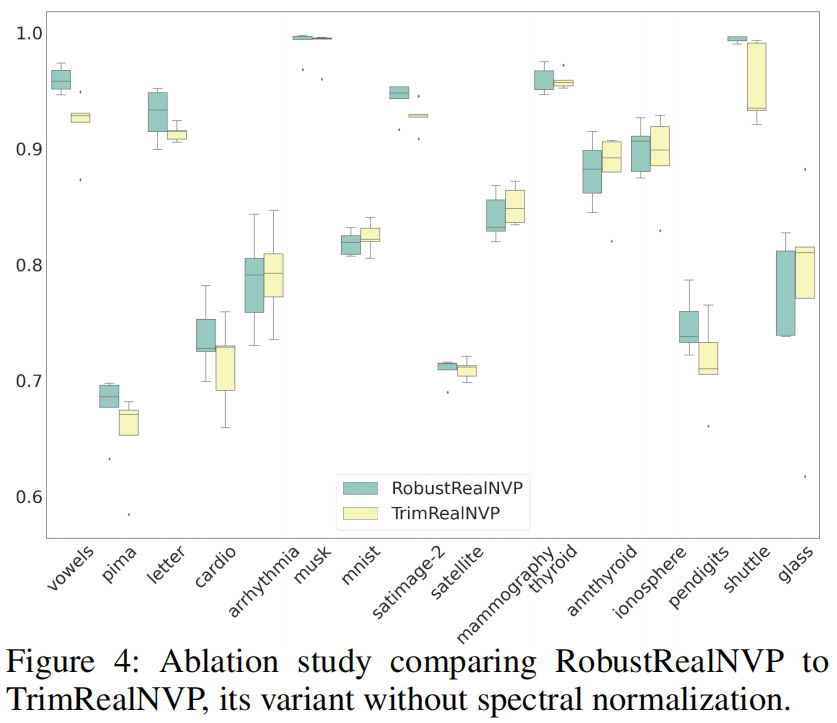
Ablation Study for Spectral Normalization

我们使用ODDS数据集进行消融研究，以证明谱归一化(SN)的有效性。在图4中，我们看到RobustRealNVP在16个数据集中的8个中表现优于TrimRealNVP，并且在至少4个剩余数据集中表现相同。这些结果与合成实验结果一起证明了SN在我们的框架中的有效性。

Sensitivity Analysis

在实践中，异常比往往是未知的，这使得很难确定要丢弃的数据点的数量。为了研究被高估或低估时RobustRealNVP的稳健性，我们对CIFAR10数据集进行了敏感性分析，将估计的污染比从0.05变化到0.2(注意，真正的异常比为0.1)。图6所示的结果表明，即使异常比率高估或低估高达15%，我们的方法在大多数设置下仍然保持稳定。

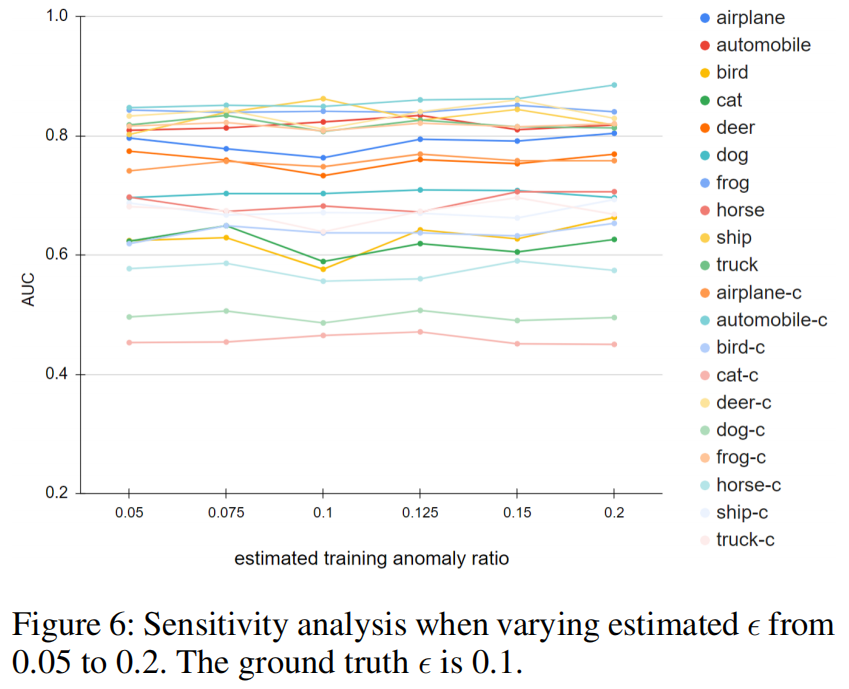
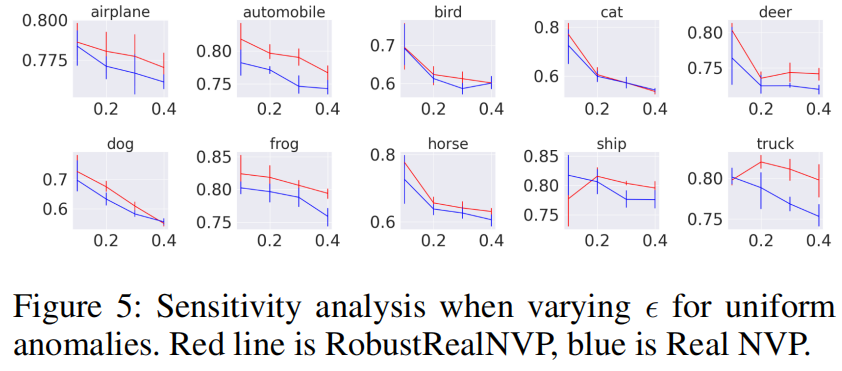
此外，我们还对真实异常比在0.1 ~ 0.4范围内变化的CIFAR10数据集进行了敏感性分析。图5所示的RealNVP和RobustRealNVP的结果表明，在大多数情况下，RobustRealNVP的表现始终优于RealNVP。

个人评述：基于 Real NVP 构建数据的概率密度函数。

对于存在异常的情况，根据Real NVP输出的概率大小，从小到大排序，丢弃密度概率小的样本，再用剩余的样本进行梯度下降，减小异常样本的影响。

对于异常聚集的情况，则用谱归一化进行处理，让整个网络满足Lipschitz=k的约束。

基于的原理就是Lipschitz假设