[论文阅读] Density estimation using real nvp

Density estimation using real nvp

参考资料：

苏剑林. (Aug. 26, 2018). 《细水长flow之RealNVP与Glow：流模型的传承与升华》[Blog post]. Retrieved from https://kexue.fm/archives/5807
《Density estimation using real nvp》
文中代码来源：https://github.com/xqding/RealNVP/tree/master

简介

生成概率模型不仅具有创建新内容的能力，而且还具有广泛的重建相关应用，包括修补、去噪、着色和超分辨率。

由于感兴趣的数据通常是高维和高度结构化的，这一领域的挑战是建立足够强大的模型来捕捉其复杂性，同时仍然是可训练的。我们通过引入 real-valued non-volume preserving（real NVP，实值非体积保持）转换 来解决这一挑战，这是一种易于处理且具有表现力的高维数据建模方法。

该模型能够对数据点进行高效准确的推断、采样和对数密度估计。此外，本文提出的体系结构可以根据该模型提取的层次特征精确有效地重建输入图像。

模型

Change of variable formula

给定一个观测数据变量 $x \in X$。一个隐变量 $z \in Z$ 上的简单先验概率分布 $p_Z$，一个双射 $f:X\rightarrow Z(g = f^{-1})$，变量变换公式定义了 $x$ 上的模型分布：

\[p_X(x)=p_Z(f(x))\left| \text{det} \left( \frac{\partial f(x)}{\partial x^T} \right) \right| \tag{2} \]

\[log(p_X(x))=log(P_Z(f(x)))+log\left( \left| \text{det}\left( \frac{\partial f(x)}{\partial x^T} \right) \right| \right) \tag{3} \]

其中 $\frac{\partial f(x)}{\partial x^T}$ 是函数 $f$ 关于 $x$ 的的雅克比矩阵

在隐空间中绘制了一个样本 $z \sim p_Z$，它的逆的像 $x=f^{-1}(z)=g(z)$ 生成了一个原空间的样本。计算点 $x$ 上的密度，可以通过计算它的像 $f(x)$ 密度并乘以相关的雅克比行列式 $ \text{det} \left( \frac{\partial f(x)}{\partial x^T} \right)$ 得到。如图1所示

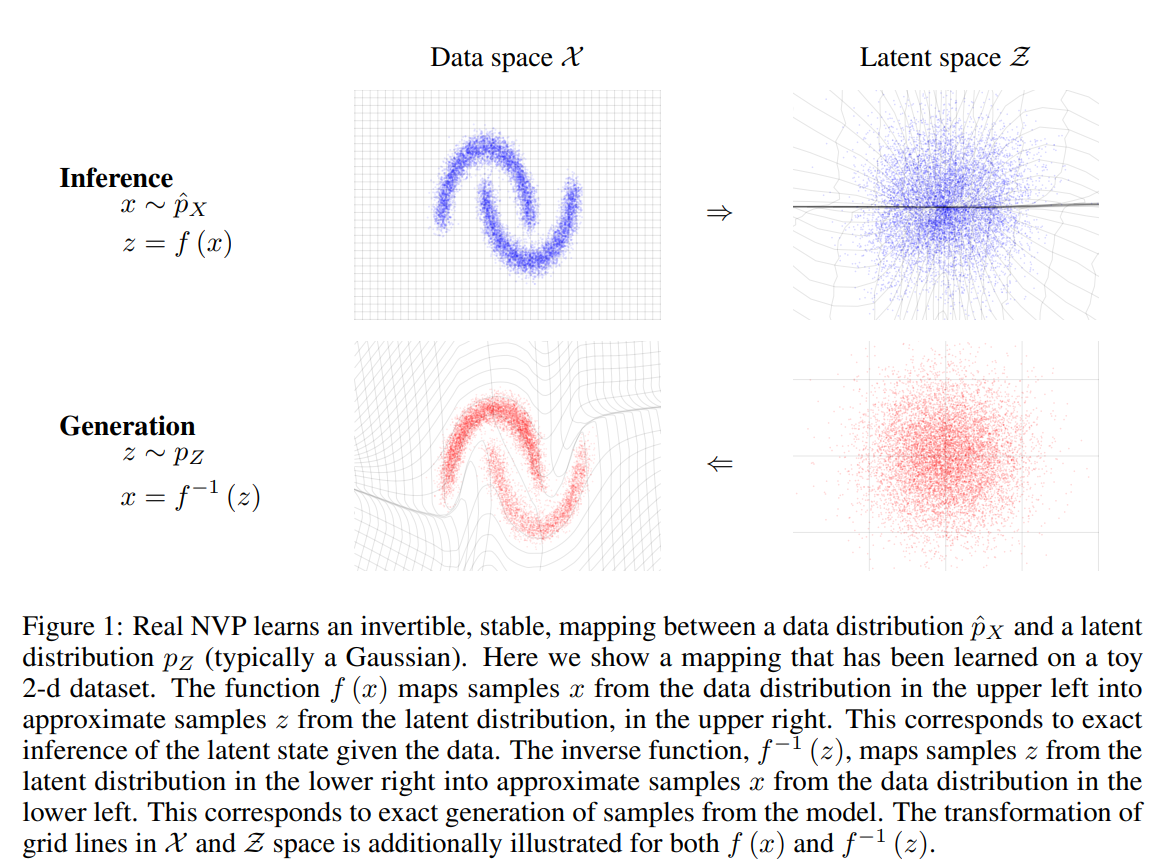
耦合层

通过对函数 $f$ 的精心设计，可以学习到一个双射模型，该模型既易于处理，又非常灵活。由于计算变换的雅可比行列式对于有效地训练使用这个原理是至关重要的，这项工作利用了一个简单的观察，即三角形矩阵的行列式可以有效地计算为其对角线项的乘积。

我们将通过叠加一系列简单的双射函数来构建一个灵活且易于处理的双射函数。在每个简单的双射中，输入向量的$x_{d+1:D}$部分使用一个函数更新，这个函数很容易求逆，但它以复杂的方式依赖于输入向量的剩余部分。我们把这些简单的双射称为一个仿射耦合层。给定 $D$ 维输入$x$ 和 $d<D$，仿射耦合层的输出 $y$ 符合方程：

\[\begin{align} y_{1:d}&=x_{1:d} \tag{4}\\ y_{d+1:D}&=x_{d+1:D}\odot exp(s(x_{1:d}))+t(x_{1:d}) \tag{5} \end{align} \]

其中 $s$ 和 $t$ 表示缩放和平移，两个函数均为 $R^d \mapsto R^{D-d}$。 $\odot$ 代表哈达玛积乘积。

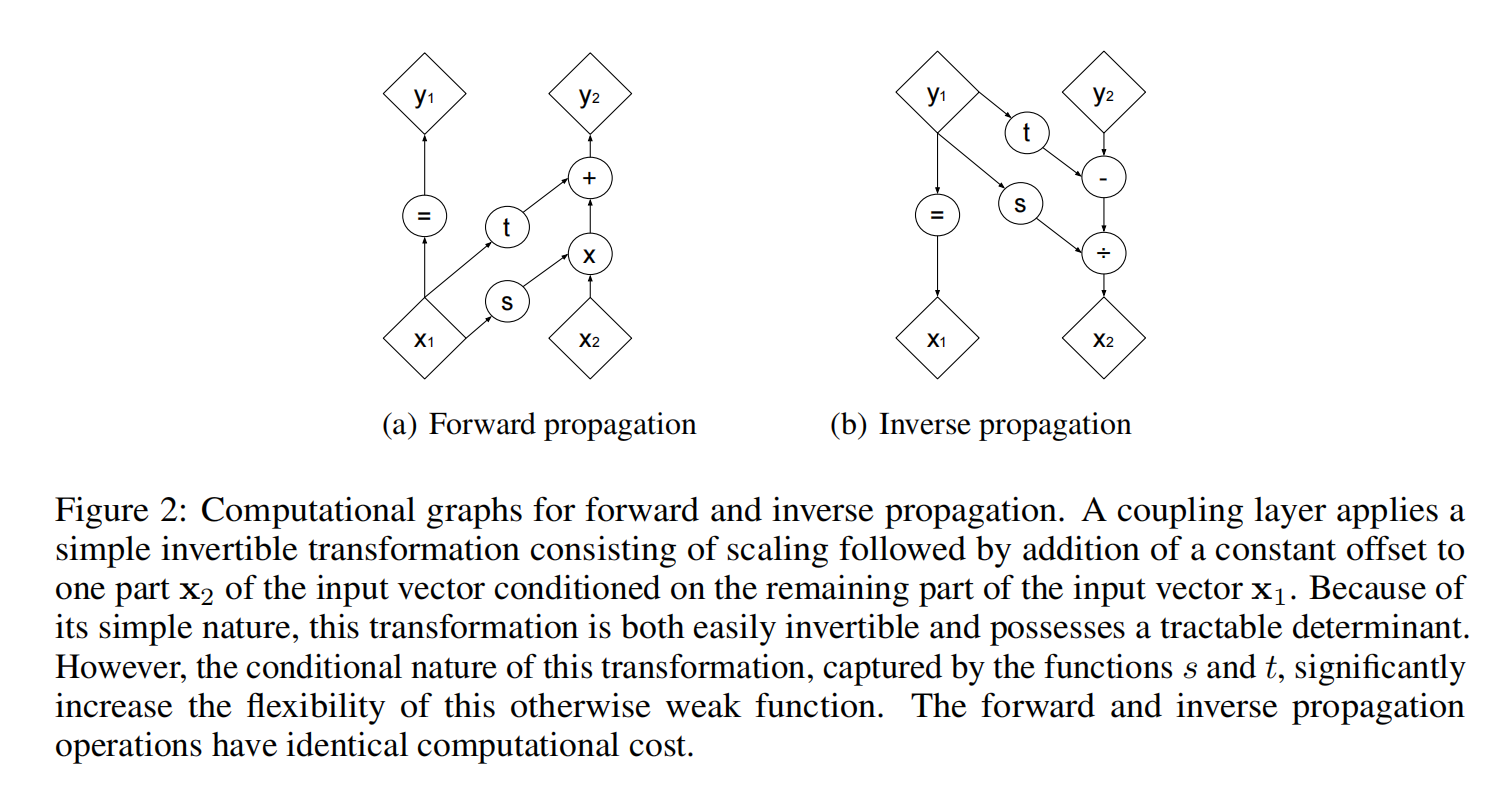
具体如图2(a)所示， $x_1$ 对应 $x_{1:d}$，$x_2$ 对应 $x_{d+1:D}$。公式(5)相当于对 $x_2$ 进行一个仿射变换。

雅克比矩阵

该变换的雅克比矩阵如下：

\[\frac{\partial y}{\partial x^T}=\begin{bmatrix} \mathbb{I}_d & 0\\ \frac{\partial y_{d+1:D}}{\partial x^T_{1:d}} & diag(exp[s(x_{1:d})]) \end{bmatrix} \tag{6} \]

该雅克比矩阵的行列式为 $exp(\sum_js(x_{1:d})_j)$。由于计算耦合层运算的雅可比行列式不涉及计算s或t的雅可比行列式，因此这些函数可以任意复杂。在本文我们使用深度卷积网络。

计算这些耦合层的逆函数并不比前向传播复杂，这意味着对于这个模型，采样和推理一样有效。其公式表达如下：

\[\begin{cases} y_{1:d}&=x_{1:d}\\ y_{d+1:D}&=x_{d+1:D}\odot exp(s(x_{1:d}))+t(x_{1:d})\\ \end{cases}\\\tag{7} \]

\[\Leftrightarrow \begin{cases} x_{1:d}&=y_{1:d}\\ x_{d+1:D}&=(y_{d+1:D} - t(y_{1:d})) \odot exp(-s(y_{1:d}))\\ \end{cases}\\\tag{8} \]

具体如图2(b)所示。主要是 $y_1=x_1$，导致倒推十分方便。

耦合层组合

尽管耦合层功能强大，但它们的正向转换会使某些组件保持不变，如下图所示。

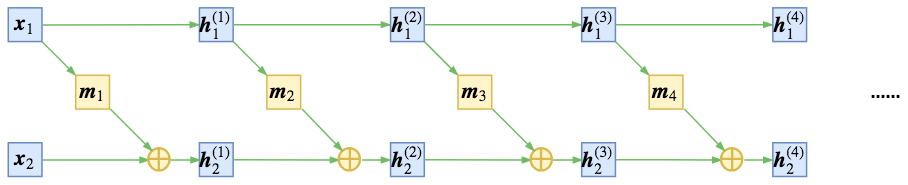
简单的耦合使得其中一部分仍然保持恒等，信息没有充分混合

这个困难可以通过交替组合耦合层来克服，这样在一个耦合层中保持不变的组件在下一个耦合层中更新。如下图所示。

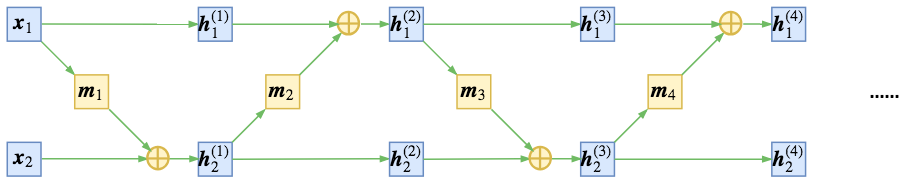
通过交叉耦合，充分混合信息，达到更强的非线性

最后的得到的雅克比行列式也是容易计算的

\[\frac{\partial (f_b \circ f_a)}{\partial x_a^T}(x_a)=\frac{\partial f_a}{\partial x_a^T}(x_a)\cdot\frac{\partial f_b}{\partial x_b^T}(x_b=f_a(x_a)) \tag{10} \]

\[\det(A \cdot B)=\det(A)\det(B) \tag{11} \]

类似的，它的逆函数也能容易计算得到

\[(f_b \circ f_a)^{-1}=f_a^{-1} \circ f_b^{-1} \tag{12} \]

耦合层代码示例

参考代码：https://github.com/xqding/RealNVP/tree/master

此处的代码比较简单，只考虑了数据是2维的情况。

class Affine_Coupling(nn.Module):
    def __init__(self, mask, hidden_dim):
        super(Affine_Coupling, self).__init__()
        self.input_dim = len(mask)
        self.hidden_dim = hidden_dim

        ## mask to seperate positions that do not change and positions that change.
        ## mask[i] = 1 means the ith position does not change.
        self.mask = nn.Parameter(mask, requires_grad = False)

        ## layers used to compute scale in affine transformation
        self.scale_fc1 = nn.Linear(self.input_dim, self.hidden_dim)
        self.scale_fc2 = nn.Linear(self.hidden_dim, self.hidden_dim)
        self.scale_fc3 = nn.Linear(self.hidden_dim, self.input_dim)
        self.scale = nn.Parameter(torch.Tensor(self.input_dim))
        init.normal_(self.scale)

        ## layers used to compute translation in affine transformation 
        self.translation_fc1 = nn.Linear(self.input_dim, self.hidden_dim)
        self.translation_fc2 = nn.Linear(self.hidden_dim, self.hidden_dim)
        self.translation_fc3 = nn.Linear(self.hidden_dim, self.input_dim)

    def _compute_scale(self, x):
        ## compute scaling factor using unchanged part of x with a neural network
        s = torch.relu(self.scale_fc1(x*self.mask))
        s = torch.relu(self.scale_fc2(s))
        s = torch.relu(self.scale_fc3(s)) * self.scale        
        return s

    def _compute_translation(self, x):
        ## compute translation using unchanged part of x with a neural network        
        t = torch.relu(self.translation_fc1(x*self.mask))
        t = torch.relu(self.translation_fc2(t))
        t = self.translation_fc3(t)        
        return t
    
    def forward(self, x):
        ## convert latent space variable to observed variable
        s = self._compute_scale(x)
        t = self._compute_translation(x)
        
        y = self.mask * x + (1 - self.mask) * (x * torch.exp(s) + t)        
        logdet = torch.sum((1 - self.mask)*s, -1)
        
        return y, logdet

    def inverse(self, y):
        ## convert observed varible to latent space variable
        s = self._compute_scale(y)
        t = self._compute_translation(y)
                
        x = self.mask * y + (1 - self.mask) * ((y - t) * torch.exp(-s))
        logdet = torch.sum((1 - self.mask)*(-s), -1)
        
        return x, logdet

scale_fc1，scale_fc1，scale_fc1 为当前耦合层的函数 $s$ 对应的神经网络

translation_fc1，translation_fc2，translation_fc3 为当前耦合层的函数 $t$ 对应的神经网络

self.mask 起到将 $x$ 划分成 $x_1,x_2$ 的作用，其中 $x_1$ 对应 $x_{1:d}$，$x_2$ 对应 $x_{d+1:D}$

此处 forward 函数将隐空间变量 $z$ 转换成观察到的样本 $x$ ；inverse 函数则相反，将观察到的样本 $x$ 转换成隐空间变量 $z$

logdet 表示当前耦合层所对应函数的雅克比行列式的对数值。

已知样本，求样本所对应的概率密度，相当于将样本 $x$ 转换成 $z$ ，使用的是 inverse 函数，函数中 logdet 对应公式3 的 $log\left( \left| \text{det}\left( \frac{\partial f(x)}{\partial x^T} \right) \right| \right)$，损失函数即为样本 $x$ 的似然估计的相反数，具体如下：

先求隐变量 $z$ 所对应的正态分布的概率，再加上经过一系列耦合层后，所有雅克比行列式的对数值的和 logdet_tot，最后取相反数

for idx_step in range(num_steps):
    ## sample data from the scipy moon dataset
    X, label = datasets.make_moons(n_samples = 512, noise = 0.05)
    X = torch.Tensor(X).to(device = device)

    ## transform data X to latent space Z
    z, logdet_tot = realNVP.inverse(X)

    ## calculate the negative loglikelihood of X
    loss = torch.log(z.new_tensor([2*math.pi])) + torch.mean(torch.sum(0.5*z**2, -1) - logdet_tot)
    
    optimizer.zero_grad()
    loss.backward()
    
    optimizer.step()

已知样本 $x$ 的概率密度函数，需要生成$x$，相当于将 $z$ 转换成样本 $x$ 的过程，使用的是 forward 函数，函数中 logdet 对应 $log\left( \left| \text{det}\left( \frac{\partial g(z)}{\partial z^T} \right) \right| \right)$，损失函数为隐变量 $z$ 的似然估计的相反数，具体如下：

先求出 $z$ 生成的 $x$ 对应的概率密度，再加上经过一系列耦合层后，所有雅克比行列式的对数值的和 logdet_tot，最后取相反数

for idx_step in range(num_steps):
    Z = torch.normal(0, 1, size = (1024, 2))
    Z = Z.cuda()
    X, logdet = realNVP(Z)

    logp = -compute_U(X)
    loss = torch.mean(-logdet - logp)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

带掩蔽的卷积

flow中的两个操作：

将输入分割为两部分 $x_1,x_2$ ，然后输入到耦合层中，而模型中的 $s,t$ 事实上只对 $x_1$ 进行处理；
特征输入耦合层之前，要随机打乱原来特征的各个维度（相当于乱序的特征）。这两个操作都会破坏局部相关性，比如分割操作有可能割裂原来相邻的像素，随机打乱也可能将原来相邻的两个像素分割得很远。

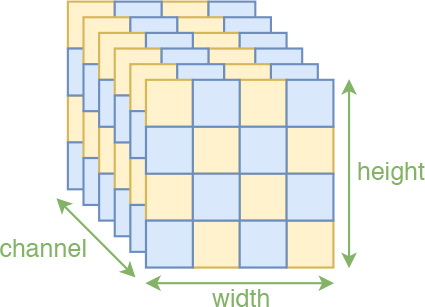
RealNVP约定分割和打乱操作，都只对“通道”轴执行。也就是说，沿着通道将输入分割为 $x_1,x_2$后，$x_1$还是具有局部相关性的。还有沿着通道按着同一方式打乱整体后，空间部分的相关性依然得到保留，因此在模型 $s,t$ 中就可以使用卷积了。

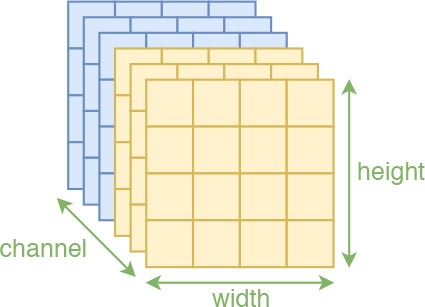
沿着通道轴进行分割，不损失空间上的局部相关性

在RealNVP中，将输入分割为两部分的操作称为mask，因为这等价于用0/1来区别标注原始输入。

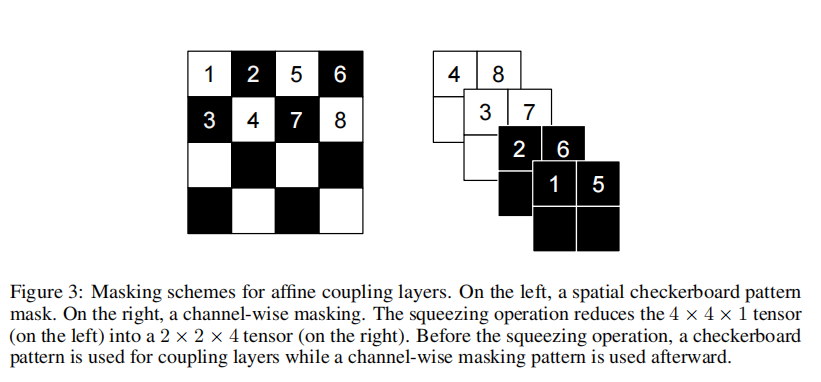
除了前面说的通过通道轴对半分的mask外，RealNVP事实上还引入了一种空间轴上的交错mask，如下图。这种mask称为棋盘式mask（格式像国际象棋的棋盘）。这种特殊的分割也保留了空间局部相关性，原论文中是两种mask方式交替使用的，但这种棋盘式mask相对复杂，也没有什么特别明显的提升，所以在Glow中已经被抛弃。

沿着空间轴交错（棋盘）分割，也是一种保持空间局部相关性的方案

分区可以使用二进制掩码 $b$ 实现，使用 $y$ 的函数形式如下：

\[y=b\odot x + (1-b) \odot (x \odot \exp(s(b\odot x))+t(b \odot x)) \tag{9} \]

多尺度结构

squeeze操作

RealNVP使用squeeze操作实现了一个多尺度架构：对于每个通道，它将图像划分为 $2 \times 2 \times c$ 形状的子正方形，然后将它们重新塑造为 $1 \times 1 \times 4c$ 形状的子正方形。压缩操作将 $h \times w \times c$ 张量转换为 $\frac{h}{2} × \frac{w}{2} × 4c$ 的张量，有效地用空间大小交换通道数量。

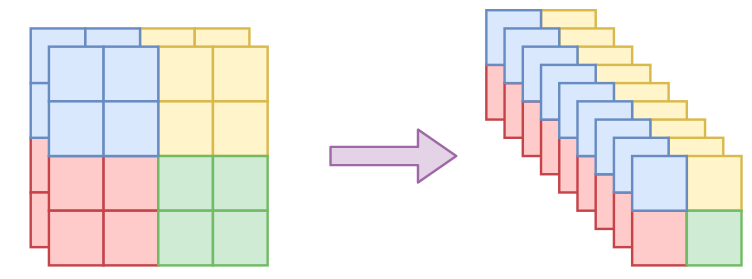
squeeze操作图示，其中2x2的小区域可以换为自定义大小的区域

多尺度结构

在所有耦合层中传播 $D$ 维向量会很麻烦，这涉及到计算和内存成本，以及需要训练的参数数量。RealNVP的每一步的多尺度操作直接将数据尺寸减少到原来的一半。如图所示。

原始输入经过第一步flow运算（“flow运算”指的是多个仿射耦合层的复合）后，输出跟输入的大小一样，这时候将输入对半分开两半$z_1,z_2$ （自然也是沿着通道轴），其中 $z_1$ 直接输出，而只将 $z_2$ 送入到下一步flow运算，后面的依此类推。比如图中的特例，最终的输出由 $z_1,z_3,z_5$ 组成，总大小跟输入一样。

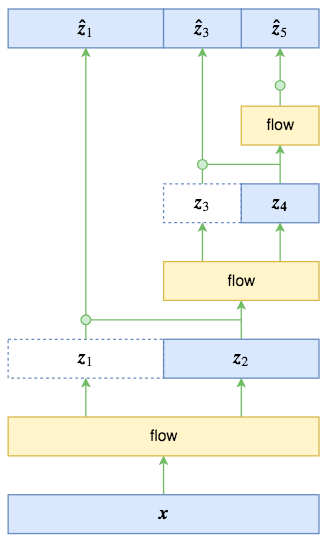
RealNVP中的多尺度结构图示

具体公式如下：

\[h^{(0)}=x\\ (z^{(i+1)},h^{(i+1)})=f^{(i+1)}(h^{(i)})\\ z^{(L)}=f^{(L)}(h^{(L-1)})\\ z=(z^{(1)},\dots,z^{(L)}) \]

最终输出的先验分布

该部分完全搬运《细水长flow之RealNVP与Glow：流模型的传承与升华》一文中的内容。

事实上，作为不同位置的多尺度输出，$z_1,z_3,z_5$的地位是不对等的，而如果直接设一个总体的标准正态分布，那就是强行将它们对等起来，这是不合理的。最好的方案，应该是写出条件概率公式

\[p(z_1,z_3,z_5)=p(z_1|z_3,z_5)p(z_3|z_5)p(z_5) \]

由于 $z_3,z_5$ 是由 $z_2$ 完全决定的，$z_5$ 也是由 $z_4$ 完全决定的，因此条件部分可以改为

\[p(z_1,z_3,z_5)=p(z_1|z_2)p(z_3|z_4)p(z_5) \]

RealNVP和Glow假设右端三个概率分布都是正态分布，其中 $p(z_1|z_2)$ 的均值方差由 $z_2$ 算出来（可以直接通过卷积运算，这有点像VAE），$p(z_3|z_4)$的均值方差由$z_4$ 算出来，$p(z_5)$ 的均值方差直接学习出来。

显然这样的假设会比简单认为它们都是标准正态分布要有效得多。我们还可以换一种表述方法：上述的先验假设相当于做了如下的变量代换

\[\hat{z}_1=\frac{z_1-\mu(z_2)}{\sigma(z_2)},\hat{z}_3=\frac{z_3-\mu(z_4)}{\sigma(z_4)}, \hat{z}_5=\frac{z_5-\mu}{\sigma} \]

然后认为 $[\hat{z}_1,\hat{z}_3,\hat{z}_5]$ 服从标准正态分布。同NICE的尺度变换层一样，这三个变换都会导致一个非1的雅可比行列式，也就是要往loss中加入形如 $\sum_{i=1}^D{log \sigma_i}$ 的这一项。

咋看之下多尺度结构就是为了降低运算量，但并不是那么简单。由于flow模型的可逆性，输入输出维度一样，事实上这会存在非常严重的维度浪费问题，这往往要求我们需要用足够复杂的网络去缓解这个维度浪费。多尺度结构相当于抛弃了 p(z) 是标准正态分布的直接假设，而采用了一个组合式的条件分布，这样尽管输入输出的总维度依然一样，但是不同层次的输出地位已经不对等了，模型可以通过控制每个条件分布的方差来抑制维度浪费问题（极端情况下，方差为0，那么高斯分布坍缩为狄拉克分布，维度就降低1），条件分布相比于独立分布具有更大的灵活性。而如果单纯从loss的角度看，多尺度结构为模型提供了一个强有力的正则项（相当于多层图像分类模型中的多条直连边）。

在 https://github.com/xqding/RealNVP/tree/master 中的代码，只假设了$z$ 服从标准正态分布。

posted @ 2023-04-12 09:54 Un-Defined 阅读(552) 评论(0) 编辑收藏举报

刷新页面返回顶部

UnDefined

[论文阅读] Density estimation using real nvp

Density estimation using real nvp

简介

相关工作

模型

Change of variable formula

耦合层

雅克比矩阵

耦合层组合

耦合层代码示例

带掩蔽的卷积

多尺度结构

squeeze操作

多尺度结构

最终输出的先验分布

公告