遗传算法详解(LINGO及MatlabGA工具箱求解实现)

遗传算法

1.前言

遗传算法是一种基于生物界自然群体遗传进化机制的自适应全局优化概率搜索算法。它与传统算法不同，不依赖梯度信息，而是通过模拟自然进化过程来搜索最优解。

例子：兔子的遗传进化

有人说，现代医学阻碍了人类的进化？你怎么看？

2．发展历程

遗传算法由密歇根大学的约翰·霍兰德和他的同事于二十世纪六十年代在对细胞自动机（英文：cellular automata）进行研究时率先提出。在二十世纪八十年代中期之前，对于遗传算法的研究还仅仅限于理论方面，直到在匹兹堡召开了第一届世界遗传算法大会。随着计算机计算能力的发展和实际应用需求的增多，遗传算法逐渐进入实际应用阶段。1989年，纽约时报作者约翰·马科夫写了一篇文章描述第一个商业用途的遗传算法--进化者（英文：Evolver）。之后，越来越多种类的遗传算法出现并被用于许多领域中，财富杂志500强企业中大多数都用它进行时间表安排、数据分析、未来趋势预测、预算、以及解决很多其他组合优化问题。

3．应用领域

4．适用问题

全局最优化问题（用其他优化方法较难求解，通常选择GA和LINGO）

5．算法详解

刚才说到了遗传算法的来源与基础，下面我们来具体说一说生物进化与遗传算法名词的对应关系。

5.1 对应关系

生物进化	遗传算法
环境	适应函数
适者生存	适应函数值最大的解被保留的概率最大
个体	问题的一个解
染色体	解的编码
基因	编码的元素
种群	根据适应函数选择的一组解
交叉（交配）	以一定的方式由双亲产生后代的过程
变异	编码的某些分量发生变化的过程

了解了上面的对应关系之后，我们再一起来看遗传算法究竟是怎么实现的。

5.2 算法思想

遗传算法是从代表问题可能潜在解集的一个种群(population)

开始的，而一个种群则由经过基因编码(coding)的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。为了简化，往往采用二进制编码。对种群反复进行选择(selection)、交叉(crossover)、变异(mutation)操作，估计各个体的适应值(fitness)，根据”适者生存、优胜劣汰”的进化规则，产生最好的种群，使适应性好的个体比适应性差的个体有更多的繁殖机会。最后把末代种群中的最优个体经过解码(decoding),可以获得满足要求的最优解。

5.3流程图描述

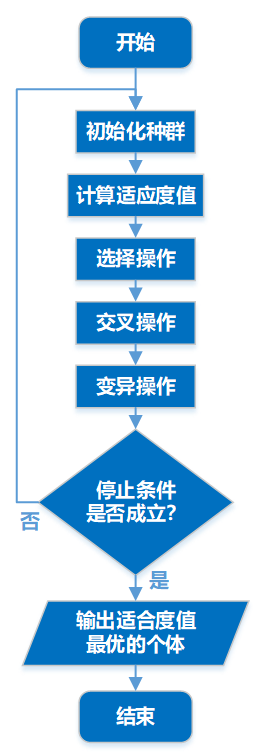
5.4 伪代码描述

(1) 随机产生初始种群;

(2) 计算种群体中每个个体的适应度值,判断是否满足停

止条件，若不满足，则转第(3)步,否则转第(7)步;

(3) 按由个体适应值所决定的某个规则选择将进入下一代

的个体;

(4) 按交叉概率Pc进行交叉操作,生产新的个体;

(5) 按变异概率Pm进行变异操作,生产新的个体;

(6) 输出种群中适应度值最优的染色体作为问题的满意解

或最优解。

Ø 具体讲解

遗传算法的具体实现

问题

如何进行编码？

如何产生初始种群？

如何定义适应函数？

如何进行遗传操作(复制、交叉、变异)？

如何产生下一代种群？

如何定义停止准则？

6．例题解析

6.1 例1：求解多变量多约束非线性规划问题

求解以下问题的解

函数图像：

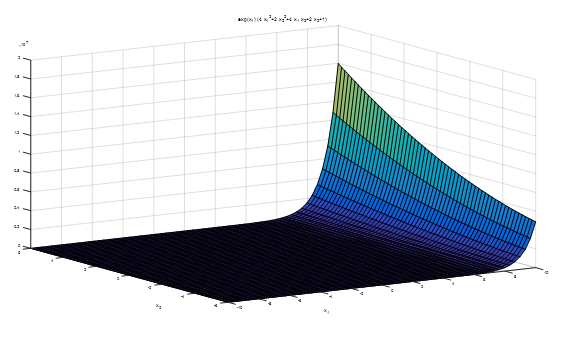
解法：

这题属于规划类问题，我们可以用LINGO来求解。

(1) 在LINGO中求解：

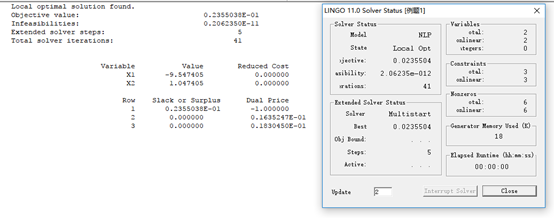
那么在遗传算法里面我们要怎么样去解决它呢？

(2) 在MATLAB中求解(GA工具箱求解)：

这里使用到的是MATLAB自带的GA工具箱，即GADS工具箱。

遗传工具箱共有四大版本，分别是

英国Sheffield《genetic arithmetic toolbox》(GATBX遗传算法工具箱)

中国陈益《simple genetic algorithms laboratory》(SGALAB简单遗传算法实验室)

美国NCSU-IE《Genetic Algorithm Optimization Tool》(GAOT遗传算法优化工具箱)

美国MathWorks《Genetic Algorithm and Direct Search Toolbox 》(GADS遗传算法和直接搜索工具箱)

6.2 例2：求解最值问题

求解以下问题

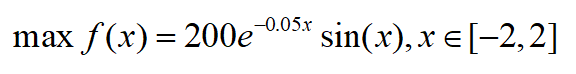
函数图像为

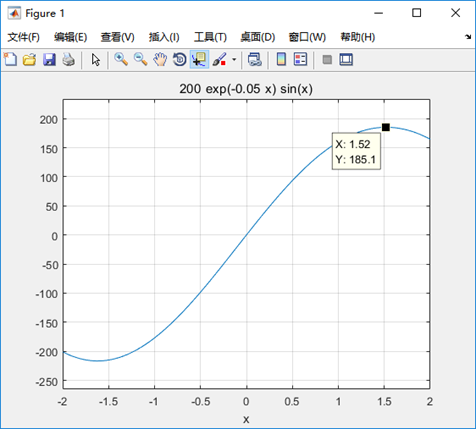
最大值大约在x=1.5附近取得。

(1) 在LINGO中求解：

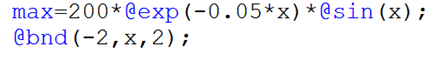
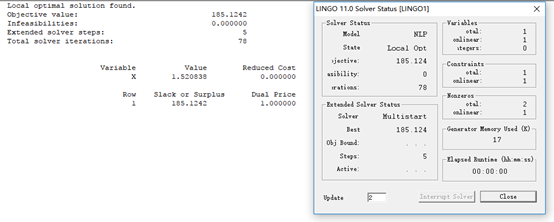
(2) 在MATLAB中求解：

第一种方法：使用GA工具箱

注意：GA工具箱默认求最小值！若要求最大值，需要加上负号！

代码实现如下：

%主程序代码,本程序采用遗传算法接力进化，
%将上次进化结束后得到的最终种群作为下次输入的初始种群
%主程序代码,
clc;
close all;
clear all;

% 进化的代数
T=50;
% 初始的种群
options=gaoptimset('Generations',T);
[x,fval,reason,output,final_pop]=ga(@fitnessfun,1,options);

%进行第二次接力进化
options1=gaoptimset('Generations',T,'InitialPopulation',final_pop,'PlotFcns',@gaplotbestf);
[x,fval,reason,output,final_pop]=ga(@fitnessfun,1,options1);

Bestx=x
BestFval=-fval


% 适应度函数
function f = fitnessfun(x)
    if(x<-2|x>2)
        f=100;
    else
        f=-200*exp(-0.05*x)*sin(x);
    end
end

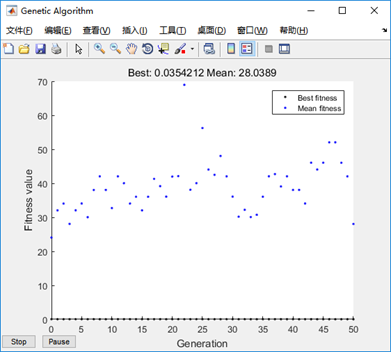
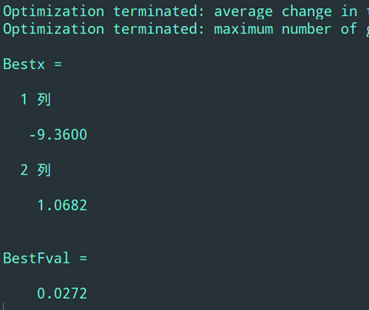
生成结果如下：

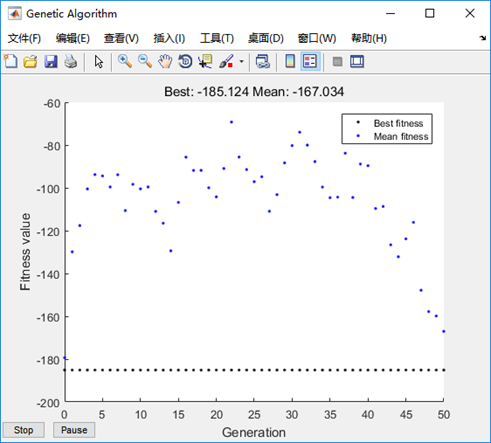
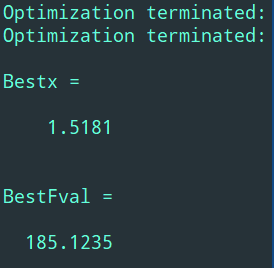
要点：适应度函数的选取

第二种方法：使用GA工具箱GUI（有可能在将来的版本中移除）

这里我给大家实际演示一下。

要点

第三种方法：自定义实现遗传算法

接下来就步入正题了，因为工具箱提供的功能有限，很多时候不能很好地满足我们的需要，那我们怎么自己实现一个遗传算法呢？

代码实现如下：

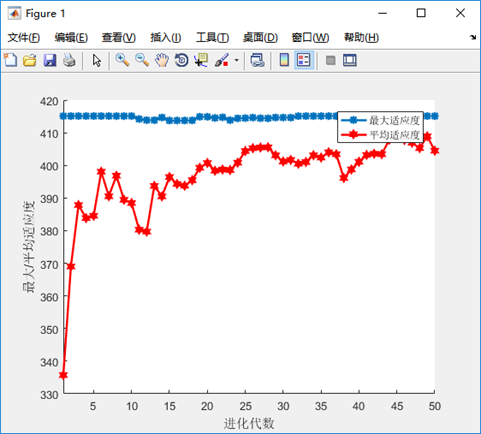
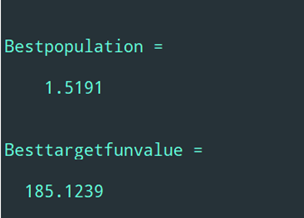
%主程序代码,本程序采用遗传算法接力进化，
%将上次进化结束后得到的最终种群作为下次输入的初始种群
clc;
close all;
clear all;

%进化的代数
T=100;
optionsOrigin=gaoptimset('Generations',T);
[x,fval,reason,output,finnal_pop]=ga(@fitnessfun,2,optionsOrigin);

%进行第二次接力进化
options1=gaoptimset('Generations',T,'InitialPopulation',finnal_pop,'PlotFcns',@gaplotbestf);
[x,fval,reason,output,finnal_pop,trace]=ga(@fitnessfun,2,options1);

Bestx=x
BestFval=fval


% 适应度函数
function f = fun(x)
    g1=1.5+x(1)*x(2)-x(1)-x(2);
    g2=-x(1)*x(2)-10;
    if (g1>0|g2>0)
        f=100;
    else
        f=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);;    
    end
end

%主程序：
%用遗传算法求解y=200*exp(-0.05*x).*sin(x)在[-2 2]区间上的最大值
clc;
clear all;
close all;

global BitLength
global boundsbegin
global boundsend
bounds=[-2 2];%一维自变量的取值范围
precision=0.0001; %运算精度
boundsbegin=bounds(:,1);
boundsend=bounds(:,2);
%计算如果满足求解精度至少需要多长的染色体
BitLength=ceil(log2((boundsend-boundsbegin)' ./ precision));
popsize=50; %初始种群大小

Generationnmax=100;  %最大代数
pcrossover=0.90; %交配概率
pmutation=0.09; %变异概率
%产生初始种群
population=round(rand(popsize,BitLength));
%计算适应度,返回适应度Fitvalue和累积概率cumsump
[Fitvalue,cumsump]=fitnessfun(population);  
Generation=1;
while Generation<Generationnmax+1
   for j=1:2:popsize 
      %选择操作
      seln=selection(population,cumsump);
      %交叉操作
      scro=crossover(population,seln,pcrossover);
      scnew(j,:)=scro(1,:);
      scnew(j+1,:)=scro(2,:);
      %变异操作
      smnew(j,:)=mutation(scnew(j,:),pmutation);
      smnew(j+1,:)=mutation(scnew(j+1,:),pmutation);
   end
   population=smnew;  %产生了新的种群
   %计算新种群的适应度   
   [Fitvalue,cumsump]=fitnessfun(population);
   %记录当前代最好的适应度和平均适应度
   [fmax,nmax]=max(Fitvalue);
   fmean=mean(Fitvalue);
   ymax(Generation)=fmax;
   ymean(Generation)=fmean;
   %记录当前代的最佳染色体个体
   x=transform2to10(population(nmax,:));
   %自变量取值范围是[-2 2],需要把经过遗传运算的最佳染色体整合到[-2 2]区间
  xx=boundsbegin+x*(boundsend-boundsbegin)/(power((boundsend),BitLength)-1);
   xmax(Generation)=xx;
   Generation=Generation+1
end
Generation=Generation-1;
Bestpopulation=xx
Besttargetfunvalue=targetfun(xx)
%绘制经过遗传运算后的适应度曲线。一般地，如果进化过程中种群的平均适应度与最大适
%应度在曲线上有相互趋同的形态，表示算法收敛进行得很顺利，没有出现震荡；在这种前
%提下，最大适应度个体连续若干代都没有发生进化表明种群已经成熟。
figure(1);
hand1=plot(1:Generation,ymax);
set(hand1,'linestyle','-','linewidth',1.8,'marker','*','markersize',6)
hold on;

hand2=plot(1:Generation,ymean);
set(hand2,'color','r','linestyle','-','linewidth',1.8,...
'marker','h','markersize',6)
xlabel('进化代数');ylabel('最大/平均适应度');xlim([1 Generationnmax]);
legend('最大适应度','平均适应度');
box off;hold off;


%子程序：新种群交叉操作,函数名称存储为crossover.m
function scro=crossover(population,seln,pc);
BitLength=size(population,2);
pcc=IfCroIfMut(pc);  %根据交叉概率决定是否进行交叉操作，1则是，0则否
if pcc==1
   chb=round(rand*(BitLength-2))+1;  %在[1,BitLength-1]范围内随机产生一个交叉位
   scro(1,:)=[population(seln(1),1:chb) population(seln(2),chb+1:BitLength)];
   scro(2,:)=[population(seln(2),1:chb) population(seln(1),chb+1:BitLength)];
else
   scro(1,:)=population(seln(1),:);
   scro(2,:)=population(seln(2),:);
end  


%子程序：计算适应度函数, 函数名称存储为fitnessfun
function [Fitvalue,cumsump]=fitnessfun(population);
global BitLength
global boundsbegin
global boundsend
popsize=size(population,1);   %有popsize个个体
for i=1:popsize
   x=transform2to10(population(i,:));  %将二进制转换为十进制
    %转化为[-2,2]区间的实数
xx=boundsbegin+x*(boundsend-boundsbegin)/(power((boundsend),BitLength)-1); 
   Fitvalue(i)=targetfun(xx);  %计算函数值，即适应度
end
%给适应度函数加上一个大小合理的数以便保证种群适应值为正数
Fitvalue=Fitvalue'+230;
%计算选择概率
fsum=sum(Fitvalue);
Pperpopulation=Fitvalue/fsum;
%计算累积概率
cumsump(1)=Pperpopulation(1);
for i=2:popsize
   cumsump(i)=cumsump(i-1)+Pperpopulation(i);
end
cumsump=cumsump';

%子程序：新种群变异操作，函数名称存储为mutation.m
function snnew=mutation(snew,pmutation);
BitLength=size(snew,2);
snnew=snew;
pmm=IfCroIfMut(pmutation);  %根据变异概率决定是否进行变异操作，1则是，0则否
if pmm==1
   chb=round(rand*(BitLength-1))+1;  %在[1,BitLength]范围内随机产生一个变异位
   snnew(chb)=abs(snew(chb)-1);
end   


%子程序：判断遗传运算是否需要进行交叉或变异, 函数名称存储为IfCroIfMut.m
function pcc=IfCroIfMut(mutORcro);
test(1:100)=0;
l=round(100*mutORcro);
test(1:l)=1;
n=round(rand*99)+1;
pcc=test(n);  


%子程序：新种群选择操作, 函数名称存储为selection.m
function seln=selection(population,cumsump);
%从种群中选择两个个体
for i=1:2
   r=rand;  %产生一个随机数
   prand=cumsump-r;
   j=1;
   while prand(j)<0
       j=j+1;
   end
   seln(i)=j; %选中个体的序号
end


%子程序：将2进制数转换为10进制数,函数名称存储为transform2to10.m
function x=transform2to10(Population);
BitLength=size(Population,2);
x=Population(BitLength);
for i=1:BitLength-1
   x=x+Population(BitLength-i)*power(2,i);
end


%子程序：对于优化最大值或极大值函数问题，目标函数可以作为适应度函数
%函数名称存储为targetfun.m
function y=targetfun(x); %目标函数
y=200*exp(-0.05*x).*sin(x);