图的简单应用(C/C++实现)
存档:
1 #include <stdio.h> 2 #include <stdlib.h> 3 #define maxv 10//定义最大顶点数 4 typedef char elem;//图中顶点的数据类型 5 #include "graph.h" 6 void main() 7 { 8 elem v0; 9 int v; 10 mgraph g; 11 printf("1.初始化函数测试:\n"); 12 initial(g); 13 printf("2.创建函数测试:\n"); 14 create(g); 15 printf("3.输出函数测试:\n"); 16 printg(g); 17 printf("4.求最短路径:\n"); 18 printf("请输出源顶点数据v0:"); 19 scanf("%c",&v0); 20 v=locate(g,v0); 21 dijkstra(g,v); 22 printf("5.输出最短路径:\n"); 23 printpath(g,v); 24 printf("\n"); 25 }
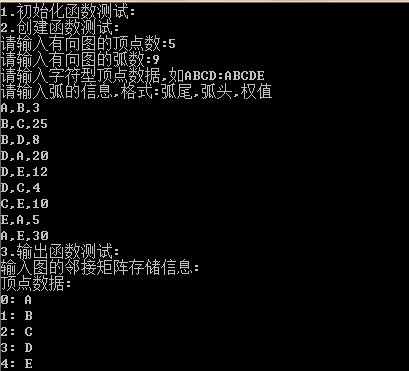
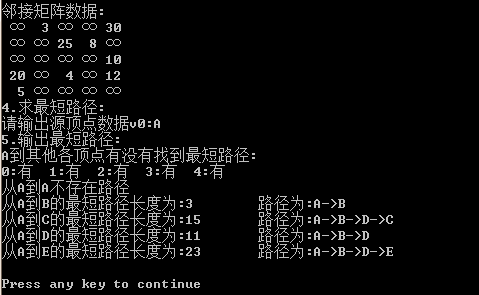
1 //有向带权网的邻接矩阵,顶点数据为字符型 2 #define inf 32767 3 typedef struct MGraph 4 { 5 elem vexes[maxv];//顶点表 6 int edges[maxv][maxv];//邻接矩阵 7 int n,e;//顶点数n和边数e 8 }mgraph; 9 void initial(mgraph &g)//初始化函数 10 { 11 int i,j; 12 g.e=0; 13 g.n=0; 14 for(j=0;j<maxv;j++)//建立顶点表 15 g.vexes[j]=0; 16 for(i=0;i<maxv;i++) 17 { 18 for(j=0;j<maxv;j++) 19 { 20 g.edges[i][j]=inf;//初始化邻接矩阵 21 } 22 } 23 } 24 int locate(mgraph g,elem u)//查找顶点对应的数组下标值 25 { 26 for(int i=0;i<g.n;i++) 27 { 28 if(g.vexes[i]==u) 29 return i; 30 } 31 return -1; 32 } 33 void create(mgraph &g)//创建有向带权网的邻接矩阵存储 34 { 35 int i,j,k,w; 36 elem u,v; 37 printf("请输入有向图的顶点数:"); 38 scanf("%d",&g.n); 39 printf("请输入有向图的弧数:"); 40 scanf("%d",&g.e); 41 fflush(stdin);//清空缓存中的数据 42 printf("请输入字符型顶点数据,如ABCD:"); 43 for(j=0;j<g.n;j++) 44 scanf("%c",&g.vexes[j]);//建立顶点表 45 fflush(stdin); 46 printf("请输入弧的信息,格式:弧尾,弧头,权值\n"); 47 for(k=0;k<g.e;k++) 48 { 49 scanf("%c,%c,%d",&u,&v,&w); 50 i=locate(g,u); 51 j=locate(g,v); 52 g.edges[i][j]=w; 53 fflush(stdin); 54 } 55 } 56 void printg(mgraph g)//输出有向带权网的邻接矩阵 57 { 58 int i,j; 59 printf("输入图的邻接矩阵存储信息:\n"); 60 printf("顶点数据:\n"); 61 for(i=0;i<g.n;i++) 62 printf("%d: %c\n",i,g.vexes[i]); 63 printf("邻接矩阵数据:\n"); 64 for(i=0;i<g.n;i++) 65 { 66 for(j=0;j<g.n;j++) 67 { 68 if(g.edges[i][j]==inf) 69 printf(" ∞"); 70 else 71 printf("%3d",g.edges[i][j]); 72 } 73 printf("\n"); 74 } 75 } 76 int dist[maxv];//dist存当前找到的最短路径长度 77 int path[maxv];//当前找到的最短路径最后的一个中转顶点 78 bool s[maxv];//标记当前是否已求出最短路径,false表示没求出,true表示已求出 79 void dijkstra(mgraph g,int v)//迪杰斯特拉算法从顶点v到其余各顶点的最短路径 80 { 81 int mindis,i,j,u; 82 for(i=0;i<g.n;i++) 83 { 84 dist[i]=g.edges[v][i];//当前最短路径长度初始化 85 s[i]=false;//s[]标记还没求出当前路径 86 if(g.edges[v][i]<inf)//初始化当前找到的最短路径最后一个中转顶点 87 path[i]=v; 88 else 89 path[i]=-1; 90 } 91 s[v]=true;//源点编号v标记已求出最短路径 92 path[v]=0;//源点v没有前驱顶点 93 for(i=0;i<g.n;i++)//循环直到所有顶点的最短路径都求出或没有最短路径 94 { 95 mindis=inf; 96 u=-1;//存当前找到的路径最短的新顶点下标 97 for(j=0;j<g.n;j++)//选取不在s中且具有最小距离的顶点u 98 { 99 if((s[j]==false)&&(dist[j]<mindis)) 100 { 101 u=j; 102 mindis=dist[j]; 103 } 104 } 105 if(mindis<inf)//如果找到了新的最短路径 106 { 107 s[u]=true;//新选出顶点u标记为找到了最短路径 108 for(j=0;j<g.n;j++)//修改未找到最短路径顶点信息 109 { 110 if(s[j]==false) 111 { 112 if(g.edges[u][j]<inf&&dist[u]+g.edges[u][j]<dist[j]) 113 { 114 dist[j]=dist[u]+g.edges[u][j];//修改当前最短路径长度 115 path[j]=u;//修改当前最短路径最后一个中转点 116 } 117 } 118 } 119 } 120 } 121 } 122 void printpath(mgraph g,int v)//输出最短路径和最短路径长度 123 { 124 int i,j,w; 125 int road[maxv];//为输出最短路径做临时存储 126 printf("%c到其他各顶点有没有找到最短路径:\n",g.vexes[v]); 127 for(i=0;i<g.n;i++) 128 { 129 if(s[i]) 130 printf("%d:有 ",i); 131 else 132 printf("%d:无 ",i); 133 } 134 printf("\n"); 135 for(i=0;i<maxv;i++) 136 road[i]=-1; 137 for(i=0;i<g.n;i++) 138 { 139 if((s[i]==true)&&(i!=v))//当前顶点有最短路径,并且不是源点 140 { 141 printf("从%c到%c的最短路径长度为:%d\t路径为:",g.vexes[v],g.vexes[i],dist[i]); 142 printf("%c->",g.vexes[v]); 143 w=path[i];//最短路径途径的顶点 144 j=0;//为实现逆转标记途径顶点数 145 while(w!=v)//回溯途径顶点 146 { 147 road[j]=w; 148 j++; 149 w=path[w]; 150 } 151 for(j--;j>=0;j--)//输出最短路径 152 { 153 printf("%c->",g.vexes[road[j]]); 154 road[j]=-1; 155 } 156 printf("%c\n",g.vexes[i]); 157 } 158 else 159 printf("从%c到%c不存在路径\n",g.vexes[v],g.vexes[i]); 160 } 161 }
运行结果如下:
作 者:Angel_Kitty
出 处:https://www.cnblogs.com/ECJTUACM-873284962/
关于作者:阿里云ACE,目前主要研究方向是Web安全漏洞以及反序列化。如有问题或建议,请多多赐教!
版权声明:本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接。
特此声明:所有评论和私信都会在第一时间回复。也欢迎园子的大大们指正错误,共同进步。或者直接私信我
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是作者坚持原创和持续写作的最大动力!
欢迎大家关注我的微信公众号IT老实人(IThonest),如果您觉得文章对您有很大的帮助,您可以考虑赏博主一杯咖啡以资鼓励,您的肯定将是我最大的动力。thx.

我的公众号是IT老实人(IThonest),一个有故事的公众号,欢迎大家来这里讨论,共同进步,不断学习才能不断进步。扫下面的二维码或者收藏下面的二维码关注吧(长按下面的二维码图片、并选择识别图中的二维码),个人QQ和微信的二维码也已给出,扫描下面👇的二维码一起来讨论吧!!!

欢迎大家关注我的Github,一些文章的备份和平常做的一些项目会存放在这里。


















【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 分享 3 个 .NET 开源的文件压缩处理库,助力快速实现文件压缩解压功能!
· Ollama——大语言模型本地部署的极速利器
· [AI/GPT/综述] AI Agent的设计模式综述