浅谈切比雪夫多项式推导及其实现模版归类
切比雪夫多项式
概述:
切比雪夫多项式是与棣美弗定理有关,以递归方式定义的一系列正交多项式序列。 通常,第一类切比雪夫多项式以符号Tn表示, 第二类切比雪夫多项式用Un表示。切比雪夫多项式 Tn 或 Un 代表 n 阶多项式。
切比雪夫多项式在逼近理论中有重要的应用。这是因为第一类切比雪夫多项式的根(被称为切比雪夫节点)可以用于多项式插值。相应的插值多项式能最大限度地降低龙格现象,并且提供多项式在连续函数的最佳一致逼近。
基本性质:
对每个非负整数n, Tn(x) 和 Un(x) 都为 n次多项式。 并且当n为偶(奇)数时,它们是关于x 的偶(奇)函数, 在写成关于x的多项式时只有偶(奇)次项。
按切比雪夫多项式的展开式:
一个N 次多项式按切比雪夫多项式的展开式为如下,多项式按切比雪夫多项式的展开可以用 Clenshaw 递推公式计算。第一类切比雪夫多项式由以下递推关系确定。
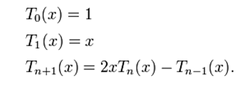
也可以用母函数表示。
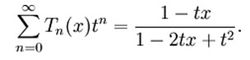
第二类切比雪夫多项式 由以下递推关系给出。
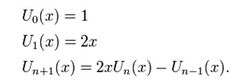
此时母函数为
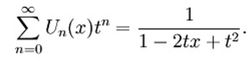
Clenshaw递推公式
在数值分析中,Clenshaw递推公式 (由Charles William Clenshaw发现)是一个求切比雪夫多项式的值的递归方法。
切比雪夫多项式
N次切比雪夫多项式,是下面形式的多项式p(x)
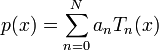
其中Tn是n阶切比雪夫多项式
Clenshaw递推公式
Clenshaw递推公式可以用来计算切比雪夫多项式的值。给定
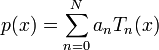
我们定义
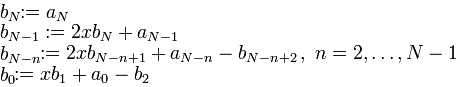
于是

(注)上面的公式在 N=0,1的情况下无意义。此时我们可以用下面的公式:

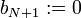
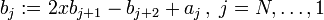
(downward, omit if N=0)
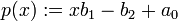
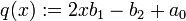
这里

或者
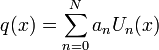
其中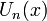 是第二类切比雪夫多项式
是第二类切比雪夫多项式
棣莫弗(de Moivre)原理
设两个复数(用三角形式表示)Z1=r1(cosθ1+isinθ1),Z2=r2(cosθ2+isinθ2),则:
Z1Z2=r1r2[cos(θ1+θ2)+isin(θ1+θ2)].
证:先讲一下复数的三角形式的概念。在复平面C上,用向量Z(a,b)来表示Z=a+bi.于是,该向量可以分成两个在实轴,虚轴上的分向量.如果向量Z与实轴的夹角为θ,这两个分向量的模分别等于rcosθ,risinθ(r=√a^2+b^2).所以,复数Z可以表示为Z=r(cosθ+isinθ).这里θ称为复数Z的辐角.
因为Z1=r1(cosθ1+isinθ1),Z2=r2(cosθ2+isinθ2),所以
Z1Z2=r1r2(cosθ1+isinθ1)(cosθ2+isinθ2)
=r1r2(cosθ1cosθ2+icosθ1sinθ2+isinθ1cosθ2-sinθ1sinθ2)
=r1r2[(cosθ1cosθ2-sinθ1sinθ2)+i(cosθ1sinθ2+sinθ1cosθ2)]
=r1r2[cos(θ1+θ2)+isin(θ1+θ2)].
其实该定理可以推广为一般形式:
设n个复数Z1=r1(cosθ1+isinθ1),Z2=r2(cosθ2+isinθ2),……,Zn=rn(cosθn+isinθn),则:
Z1Z2……Zn=r1r2……rn[cos(θ1+θ2+……+θn)+isin(θ1+θ2+……+θn)].
证:用数学归纳法即可,归纳基础就是两个复数相乘的棣莫弗定理。
如果把棣莫弗定理和欧拉(Euler)公式“e^iθ=cosθ+isinθ”(参见《泰勒公式》,严格的证明需要复分析)放在一起看,则可以用来理解欧拉公式的意义。
利用棣莫弗定理有:
Z1Z2……Zn=r1r2……rn [cos(θ1+θ2+……+θn)+isin(θ1+θ2+……+θn)]
如果可以把所有的复数改写成指数的形式,即:Z1=r1e^iθ1,Z2=r2e^iθ2,……,Zn=rne^iθn,
Z1Z2……Zn=r1r2……rn e^i(θ1+θ2+……+θn)
这和指数的可加性一致.
在一般形式中如果令Z1=Z2=……=Zn=Z,则能导出复数开方的公式.有兴趣可自己推推看.
下面这题可作为切比雪夫多项式的模版:
Trig Function
TimeLimit: 2000/1000 MS (Java/Others) Memory Limit:32768/32768 K (Java/Others)
Total Submission(s): 714 Accepted Submission(s): 206
Problem Description
f(cos(x))=cos(n∗x) holds for all x.
Given two integersn and m , you need to calculate the coefficient of x^m in f(x), modulo 998244353
Input
Multiple testcases (no more than 100).
Each test casecontains one line consisting of two integers n and m.
1≤n≤109,0≤m≤104
Output
Output the answerin a single line for each test case.
Sample Input
2 0
2 1
2 2
Sample Output
998244352
0
2
【题意】
给出一个函数,代入n,m后求出xm的系数,并取模输出。
【思路】
我们先尝试把cos(nx)化为cos(x)的形式,然后把cos(x)用x代换,就可以得到f(x)=...的形式,然后就能得到所求的系数了。
那么我们如何把cos(nx)化为cos(x)的形式呢。
其实可以尝试着暴力写出前几项的形式。如下图:
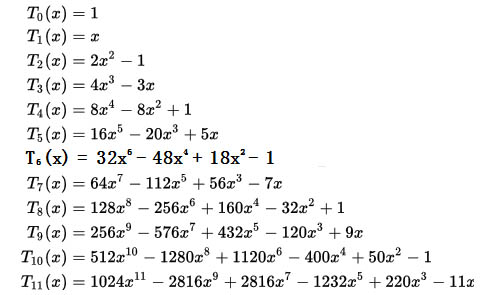
由写出的式子,我们可以发现以下几点:
- 当m大于n时,答案显然为0。
- 当n为奇数且m为偶数或n为偶数且m为奇数时答案显然为0。
- 当n为奇数,且m为1时,答案的绝对值为n。
- 当n为偶数,且m为0时,答案的绝对值为1。
- 其余情况答案的绝对值均为【 n * (n-m+2) * (n-m+4) * ... * (n+m-4) * (n+m-2) 】/(m!)。(注意逆元的运用)
- 上面出现绝对值的情况,3和4 当(n/2)%2 == 0 时符号为正,否则为负;5 当((n-m)/2)%2 == 0时,符号为正,否则符号为负。
依照这个规律分类讨论一下即可。
于是我们可以得到以下一般解析式
注意"!!"不是阶乘的阶乘,而是不超过n且与n具有相同奇偶性的所有正整数连乘积。
n分类讨论下,当n为偶数时m=2*k, n为奇数时m=2*k-1
还有注意下"!!"的约分,可能下面的比上面的大
于是我们就得到了以下代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn=1e5+5; 5 const int mod=998244353; 6 ll fac[maxn]={1}; 7 ll n,m; 8 void init() 9 { 10 for(int i=1;i<maxn;i++) 11 fac[i]=fac[i-1]*i%mod; 12 } 13 ll qmod(ll x,int q) 14 { 15 ll res=1; 16 while(q) 17 { 18 if(q%2) 19 res=res*x%mod; 20 x=x*x%mod; 21 q/=2; 22 } 23 return res; 24 } 25 int main(void) 26 { 27 init(); 28 while(~scanf("%lld%lld",&n,&m)) 29 { 30 if(m>n) 31 puts("0"); 32 else if(n%2&&m%2==0) 33 puts("0"); 34 else if(n%2==0&&m%2) 35 puts("0"); 36 else 37 { 38 ll fz=n%mod; 39 if(m>=1) 40 { 41 for(int i=n-m+1;i<=n+m-1;i++) 42 { 43 if(i%2==(n+m-2)%2) 44 { 45 fz=fz*i%mod; 46 } 47 } 48 ll tmp=fz*qmod(fac[m],mod-2)%mod; 49 if((n-m)/2%2) 50 tmp=-tmp; 51 printf("%lld\n",(tmp+mod)%mod); 52 } 53 else 54 { 55 ll t=1; 56 for(int i=n+m-1;i<=n-m;i++) 57 { 58 if(i%2==(n+m-2)%2) 59 t=t*i%mod; 60 } 61 ll tmp=fz*qmod(fac[m],mod-2)%mod*qmod(t, mod-2)%mod; 62 if((n-m)/2%2) 63 tmp=-tmp; 64 printf("%lld\n",(tmp+mod)%mod); 65 } 66 } 67 } 68 }
作 者:Angel_Kitty
出 处:https://www.cnblogs.com/ECJTUACM-873284962/
关于作者:阿里云ACE,目前主要研究方向是Web安全漏洞以及反序列化。如有问题或建议,请多多赐教!
版权声明:本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接。
特此声明:所有评论和私信都会在第一时间回复。也欢迎园子的大大们指正错误,共同进步。或者直接私信我
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是作者坚持原创和持续写作的最大动力!
欢迎大家关注我的微信公众号IT老实人(IThonest),如果您觉得文章对您有很大的帮助,您可以考虑赏博主一杯咖啡以资鼓励,您的肯定将是我最大的动力。thx.

我的公众号是IT老实人(IThonest),一个有故事的公众号,欢迎大家来这里讨论,共同进步,不断学习才能不断进步。扫下面的二维码或者收藏下面的二维码关注吧(长按下面的二维码图片、并选择识别图中的二维码),个人QQ和微信的二维码也已给出,扫描下面👇的二维码一起来讨论吧!!!

欢迎大家关注我的Github,一些文章的备份和平常做的一些项目会存放在这里。


















【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 分享 3 个 .NET 开源的文件压缩处理库,助力快速实现文件压缩解压功能!
· Ollama——大语言模型本地部署的极速利器
· [AI/GPT/综述] AI Agent的设计模式综述