AIM Tech Round 4 (Div. 2)(A，暴力，B，组合数，C，STL+排序)

A. Diversity

time limit per test：1 second
memory limit per test：256 megabytes
input：standard input
output：standard output

Calculate the minimum number of characters you need to change in the string s, so that it contains at least k different letters, or print that it is impossible.

String s consists only of lowercase Latin letters, and it is allowed to change characters only to lowercase Latin letters too.

Input

First line of input contains string s, consisting only of lowercase Latin letters (1 ≤ |s| ≤ 1000, |s| denotes the length of s).

Second line of input contains integer k (1 ≤ k ≤ 26).

Output

Print single line with a minimum number of necessary changes, or the word «impossible» (without quotes) if it is impossible.

Examples
Input
yandex
6
Output
0
Input
yahoo
5
Output
1
Input
google
7
Output
impossible
Note

In the first test case string contains 6 different letters, so we don't need to change anything.

In the second test case string contains 4 different letters: {'a', 'h', 'o', 'y'}. To get 5 different letters it is necessary to change one occurrence of 'o' to some letter, which doesn't occur in the string, for example, {'b'}.

In the third test case, it is impossible to make 7 different letters because the length of the string is 6.

题目链接：http://codeforces.com/contest/844/problem/A

题意：大概是要在长度为len的字符串中至少要存在x个不同的字符需要变换多少次

emmmm，似乎有坑的题，窝石乐志在Test 6和Test 12上连翻跟头，代码应该很清楚，看代码吧！

下面给出AC代码：

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 int a[27];
 4 int main()
 5 {
 6     string s;
 7     cin>>s;
 8     int len=s.size();
 9     int x;
10     cin>>x;
11     if(x>len)
12     {
13         printf("impossible");
14         return 0;
15     }
16     for(int i=0;i<len;i++)
17     {
18         a[s[i]-'a'+1]++;
19     }
20     int sum=0;
21     for(int i=1;i<=26;i++)
22     {
23         if(a[i]!=0)
24         {
25             a[i]=1;
26             sum++;
27         }
28     }
29     if(x<=sum)
30         cout<<0;
31     else
32         cout<<x-sum;
33     return 0;
34 }

B. Rectangles

time limit per test：1 second
memory limit per test：256 megabytes
input：standard input
output：standard output

You are given n × m table. Each cell of the table is colored white or black. Find the number of non-empty sets of cells such that:

  1. All cells in a set have the same color.
  2. Every two cells in a set share row or column.
Input

The first line of input contains integers n and m (1 ≤ n, m ≤ 50) — the number of rows and the number of columns correspondingly.

The next n lines of input contain descriptions of rows. There are m integers, separated by spaces, in each line. The number equals 0 if the corresponding cell is colored white and equals 1 if the corresponding cell is colored black.

Output

Output single integer  — the number of non-empty sets from the problem description.

Examples
Input
1 1
0
Output
1
Input
2 3
1 0 1
0 1 0
Output
8
Note

In the second example, there are six one-element sets. Additionally, there are two two-element sets, the first one consists of the first and the third cells of the first row, the second one consists of the first and the third cells of the second row. To sum up, there are 8 sets.

题目链接：http://codeforces.com/contest/844/problem/B

题目大意

求选出在同一行或同一列颜色相同的格子，共有多少种选法。

题解

杨辉三角预处理组合数，设b[i]为第i行1的个数，则： i=1n∑j=1b[i]Cjb[i]

 

 

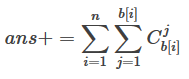
列同理，注意去掉块数为1的。

下面给出AC代码：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 const int mod=1e9+7;
 5 int mymap[55][55];
 6 int main()
 7 {
 8     int n,m;
 9     scanf("%d%d",&n,&m);
10     for(int i=1;i<=n;i++)
11     {
12         for(int j=1;j<=m;j++)
13         {
14             scanf("%d",&mymap[i][j]);
15         }
16     }
17     ll ans=n*m;
18     for(int i=1;i<=n;i++)
19     {
20         int num1=0;
21         int num2=0;
22         for(int j=1;j<=m;j++)
23         {
24             if(mymap[i][j]==1)
25                 num1++;
26             else
27                 num2++;
28         }
29         ans+=((ll)pow(2,num1)-1-num1);
30         ans+=((ll)pow(2,num2)-1-num2);
31     }
32     for(int i=1;i<=m;i++)
33     {
34         int num1=0;
35         int num2=0;
36         for(int j=1;j<=n;j++)
37         {
38             if(mymap[j][i]==1)
39                 num1++;
40             else
41                 num2++;
42         }
43         ans+=((ll)pow(2,num1)-1-num1);
44         ans+=((ll)pow(2,num2)-1-num2);
45     }
46     printf("%lld\n",ans);
47     return 0;
48 }

C. Sorting by Subsequences

time limit per test：1 second
memory limit per test：256 megabytes
input：standard input
output：standard output

You are given a sequence a1, a2, ..., an consisting of different integers. It is required to split this sequence into the maximum number of subsequences such that after sorting integers in each of them in increasing order, the total sequence also will be sorted in increasing order.

Sorting integers in a subsequence is a process such that the numbers included in a subsequence are ordered in increasing order, and the numbers which are not included in a subsequence don't change their places.

Every element of the sequence must appear in exactly one subsequence.

Input

The first line of input data contains integer n (1 ≤ n ≤ 105) — the length of the sequence.

The second line of input data contains n different integers a1, a2, ..., an ( - 109 ≤ ai ≤ 109) — the elements of the sequence. It is guaranteed that all elements of the sequence are distinct.

Output

In the first line print the maximum number of subsequences k, which the original sequence can be split into while fulfilling the requirements.

In the next k lines print the description of subsequences in the following format: the number of elements in subsequence ci (0 < ci ≤ n), then ci integers l1, l2, ..., lci (1 ≤ lj ≤ n) — indices of these elements in the original sequence.

Indices could be printed in any order. Every index from 1 to n must appear in output exactly once.

If there are several possible answers, print any of them.

Examples
Input
6
3 2 1 6 5 4
Output
4
2 1 3
1 2
2 4 6
1 5
Input
6
83 -75 -49 11 37 62
Output
1
6 1 2 3 4 5 6
Note

In the first sample output:

After sorting the first subsequence we will get sequence 1 2 3 6 5 4.

Sorting the second subsequence changes nothing.

After sorting the third subsequence we will get sequence 1 2 3 4 5 6.

Sorting the last subsequence changes nothing.

题目链接：http://codeforces.com/contest/844/problem/C

分析：排序之后,记录每个数字原来在哪里就好.可以形成环的,环的个数就是子列个数。

下面给出AC代码：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N=1e5+10;
 4 int n,a[N],sa[N],r[N];
 5 bool vis[N];
 6 bool cmp(int x,int y)
 7 {
 8     return a[x]<a[y];
 9 }
10 vector<int> v[N];
11 int main()
12 {
13     scanf("%d",&n);
14     for (int i=1;i<=n;i++)
15         scanf("%d",&a[i]),sa[i]=i;
16     sort(sa+1,sa+n+1,cmp);
17     int ans=0;
18     for (int i=1;i<=n;i++)
19     if (!vis[i])
20     {
21         ans++;
22         v[ans].push_back(i);
23         vis[i]=1;
24         for(int x=sa[i];x!=i;x=sa[x])
25             vis[x]=1,v[ans].push_back(x);
26     }
27     printf("%d\n",ans);
28     for(int i=1;i<=ans;i++)
29     {
30         printf("%d ",(int)v[i].size());
31         for(int j=0;j<v[i].size();j++)
32             printf("%d ",v[i][j]);
33         puts("");
34     }
35     return 0;
36 }

 

posted @ 2017-08-25 09:09  Angel_Kitty  阅读(406)  评论(0)  编辑  收藏  举报