Codeforces Round #336 (Div. 2)【A.思维，暴力，B.字符串，暴搜，前缀和，C.暴力，D，区间dp，E，字符串,数学】

A. Saitama Destroys Hotel

time limit per test：1 second

memory limit per test：256 megabytes

input：standard input

output：standard output

Saitama accidentally destroyed a hotel again. To repay the hotel company, Genos has volunteered to operate an elevator in one of its other hotels. The elevator is special — it starts on the top floor, can only move down, and has infinite capacity. Floors are numbered from 0 to s and elevator initially starts on floor s at time 0.

The elevator takes exactly 1 second to move down exactly 1 floor and negligible time to pick up passengers. Genos is given a list detailing when and on which floor passengers arrive. Please determine how long in seconds it will take Genos to bring all passengers to floor 0.

Input

The first line of input contains two integers n and s (1 ≤ n ≤ 100, 1 ≤ s ≤ 1000) — the number of passengers and the number of the top floor respectively.

The next n lines each contain two space-separated integers f_i and t_i (1 ≤ f_i ≤ s, 1 ≤ t_i ≤ 1000) — the floor and the time of arrival in seconds for the passenger number i.

Output

Print a single integer — the minimum amount of time in seconds needed to bring all the passengers to floor 0.

Examples

Input

3 7
2 1
3 8
5 2

Output

11

Input

5 10
2 77
3 33
8 21
9 12
10 64

Output

79

Note

In the first sample, it takes at least 11 seconds to bring all passengers to floor 0. Here is how this could be done:

1. Move to floor 5: takes 2 seconds.

2. Pick up passenger 3.

3. Move to floor 3: takes 2 seconds.

4. Wait for passenger 2 to arrive: takes 4 seconds.

5. Pick up passenger 2.

6. Go to floor 2: takes 1 second.

7. Pick up passenger 1.

8. Go to floor 0: takes 2 seconds.

This gives a total of 2 + 2 + 4 + 1 + 2 = 11 seconds.

题目链接：http://codeforces.com/contest/608/problem/A

【题意】一楼梯从最高层开始依次下降，每下一层花1s，如果该层有人，则等乘客到达后载客继续下降，乘客进电梯的时间忽略不计，给定有乘客的楼层数及乘客到达时间，求承载所有乘客下至第0层所花费的最小时间。

下面给出AC代码：

#include <bits/stdc++.h>
using namespace std;
int main()
{
    int n,m,a,b;
    cin>>n>>m;
    int t=0;
    while(n--)
    {
        cin>>a>>b;
        t=max(b-(m-a),t);
    }
    cout<<m+t<<endl;
}

B. Hamming Distance Sum

time limit per test：2 seconds

memory limit per test：256 megabytes

input：standard input

output：standard output

Genos needs your help. He was asked to solve the following programming problem by Saitama:

The length of some string s is denoted |s|. The Hamming distance between two strings s and t of equal length is defined as 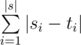, where s_i is the i-th character of s and t_i is the i-th character of t. For example, the Hamming distance between string "0011" and string "0110" is |0 - 0| + |0 - 1| + |1 - 1| + |1 - 0| = 0 + 1 + 0 + 1 = 2.

Given two binary strings a and b, find the sum of the Hamming distances between a and all contiguous substrings of b of length |a|.

Input

The first line of the input contains binary string a (1 ≤ |a| ≤ 200 000).

The second line of the input contains binary string b (|a| ≤ |b| ≤ 200 000).

Both strings are guaranteed to consist of characters '0' and '1' only.

Output

Print a single integer — the sum of Hamming distances between a and all contiguous substrings of b of length |a|.

Examples

Input

01
00111

Output

3

Input

0011
0110

Output

2

Note

For the first sample case, there are four contiguous substrings of b of length |a|: "00", "01", "11", and "11". The distance between "01" and "00" is |0 - 0| + |1 - 0| = 1. The distance between "01" and "01" is |0 - 0| + |1 - 1| = 0. The distance between "01" and "11" is |0 - 1| + |1 - 1| = 1. Last distance counts twice, as there are two occurrences of string "11". The sum of these edit distances is 1 + 0 + 1 + 1 = 3.

The second sample case is described in the statement.

题目链接：http://codeforces.com/contest/608/problem/B

【题意】给定两个字符串a,b，求b中所有跟a长度相同的子串中，各个字符与a中相应字符的差的绝对值的和。
【分析】对于字符串b中每个字符,记录该字符之前包含该字符在内的子串中0,1出现的次数。对于长度为lena的字符串a，长度为lenb的字符串b，a中第i个字符可以与b中第i到第lenb-lena+i个字符进行比较。若a中字符为0，则最后结果加上该区间内的字符为1的字符个数，若为1，则加上字符为0的个数。

下面给出AC代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int cnt[300];
int main()
{
    string a,b;
    cin>>a>>b;
    int len1=a.size();
    int len2=b.size();
    ll ans=0;
    for(int i=0;i<len2;i++)
    {
        cnt[b[i]]++;
        if(i>=len2-len1)
        {
            ans+=(len2-len1+1)-cnt[a[i-(len2-len1)]];
            cnt[b[i-(len2-len1)]]--;
        }
    }
    cout<<ans<<endl;
    return 0;
}

C. Chain Reaction

time limit per test：2 seconds

memory limit per test：256 megabytes

input：standard input

output：standard output

There are n beacons located at distinct positions on a number line. The i-th beacon has position a_i and power level b_i. When the i-th beacon is activated, it destroys all beacons to its left (direction of decreasing coordinates) within distance b_i inclusive. The beacon itself is not destroyed however. Saitama will activate the beacons one at a time from right to left. If a beacon is destroyed, it cannot be activated.

Saitama wants Genos to add a beacon strictly to the right of all the existing beacons, with any position and any power level, such that the least possible number of beacons are destroyed. Note that Genos's placement of the beacon means it will be the first beacon activated. Help Genos by finding the minimum number of beacons that could be destroyed.

Input

The first line of input contains a single integer n (1 ≤ n ≤ 100 000) — the initial number of beacons.

The i-th of next n lines contains two integers a_i and b_i (0 ≤ a_i ≤ 1 000 000, 1 ≤ b_i ≤ 1 000 000) — the position and power level of the i-th beacon respectively. No two beacons will have the same position, so a_i ≠ a_j if i ≠ j.

Output

Print a single integer — the minimum number of beacons that could be destroyed if exactly one beacon is added.

Examples

Input

4
1 9
3 1
6 1
7 4

Output

1

Input

7
1 1
2 1
3 1
4 1
5 1
6 1
7 1

Output

3

Note

For the first sample case, the minimum number of beacons destroyed is 1. One way to achieve this is to place a beacon at position 9 with power level 2.

For the second sample case, the minimum number of beacons destroyed is 3. One way to achieve this is to place a beacon at position 1337 with power level 42.

题目链接：http://codeforces.com/contest/608/problem/C

【题意】一连串灯塔，从左到右排列，位于位置a[i]的灯塔，激活后，可以破坏距离为b[i]范围内的其他灯塔，灯塔仅可向左边攻击，攻击他人自己不受损坏，受损的灯塔不能被再次激活。 现在整个排列的最右边放置一个灯塔，使得从右向左依次激活灯塔后，受破坏的灯塔个数最少。
【分析】激活最右边的灯塔之后，所有被破坏的灯塔中距离激活的灯塔最远的灯塔左边的灯塔得以存活，所以从左向右依次记录激活该灯塔后，左边剩余灯塔个数，算出最大值，用总灯塔数减去该最大值。

下面给出AC代码：

#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
int m[1000005];
int dp[1000005];
int main (void)
{
    int n;
    cin>>n;
    int x,y;
    int mins=0x3ffffff;
    int maxn=0;
    for(int i = 0; i < n; i++){
        cin>>x>>y;
        m[x]=y;
        mins=min(mins,x);
        maxn=max(maxn,x);
    }
    for(int i = mins; i <= maxn; i++){
            if(!m[i]) {dp[i]=dp[i-1]; continue;}
            if(i-m[i]-1>=0) dp[i]=dp[i-m[i]-1]+1;
            else dp[i]=1;
    }
    long long  ans=0;
    for(int i = mins; i <= maxn; i++){
       if(ans<dp[i]) ans=dp[i];
    }
    cout<<n-ans<<endl;
    return 0;
}

有一种简写，反正我没太看懂QAQ

#include<bits/stdc++.h>
using namespace std;
const int MAXA=1000002;
int n,t[MAXA],a,b[MAXA],i,ans;
int main()
{
    for(cin>>n;cin>>a;cin>>b[a+1]);
    for(i=1;i<MAXA;ans=max(ans,t[i++]))t[i]=(b[i]?(t[max(i-1-b[i], 0)]+1):t[i-1]);
    cout<<n-ans<<endl;
    return 0;
}

D. Zuma

time limit per test:2 seconds

memory limit per test:512 megabytes

input:standard input

output：standard output

Genos recently installed the game Zuma on his phone. In Zuma there exists a line of n gemstones, the i-th of which has color c_i. The goal of the game is to destroy all the gemstones in the line as quickly as possible.

In one second, Genos is able to choose exactly one continuous substring of colored gemstones that is a palindrome and remove it from the line. After the substring is removed, the remaining gemstones shift to form a solid line again. What is the minimum number of seconds needed to destroy the entire line?

Let us remind, that the string (or substring) is called palindrome, if it reads same backwards or forward. In our case this means the color of the first gemstone is equal to the color of the last one, the color of the second gemstone is equal to the color of the next to last and so on.

Input

The first line of input contains a single integer n (1 ≤ n ≤ 500) — the number of gemstones.

The second line contains n space-separated integers, the i-th of which is c_i (1 ≤ c_i ≤ n) — the color of the i-th gemstone in a line.

Output

Print a single integer — the minimum number of seconds needed to destroy the entire line.

Examples

Input

3
1 2 1

Output

1

Input

3
1 2 3

Output

3

Input

7
1 4 4 2 3 2 1

Output

2

Note

In the first sample, Genos can destroy the entire line in one second.

In the second sample, Genos can only destroy one gemstone at a time, so destroying three gemstones takes three seconds.

In the third sample, to achieve the optimal time of two seconds, destroy palindrome 4 4 first and then destroy palindrome 1 2 3 2 1.

题目链接：http://codeforces.com/contest/608/problem/D

题意:输入一个字符串；每次消去一个回文串，问最少消去的次数为多少？

思路:一般对于可以从中间操作的，一般看成是从头开始(因为只需要考虑一边)，当考虑最左边的数时，有多少中消去方法？每种消去方法对结果的贡献又是多少？同时结果的区间又是怎么变化？这就是dp式子；

1.当单独消去这个元素时，dp[l][r] = 1 + dp[l+1][r];
2.当存在一个k,l< k <= r，使得c[l] == c[k]时，可以认为在中间消除到只剩下一个回文串时，“顺带”把这一对元素消除；因为只少消到只剩下一个元素，那这个元素也是一个回文串，这时dp式子就是 dp[l][r] = dp[l+1][k-1] + dp[k+1][r];
那么当这里面的元素本来就为0呢？这就是我前面k的取值范围没有包括l的原因，这就是把[l , l + 1]当成回文串来消去，dp[l][r] = 1+dp[l+2][r];

#include<bits/stdc++.h>
using namespace std;
const int maxn=510;
int num[maxn];
int dp[maxn][maxn];
int main()
{
    int n;cin>>n;
    memset(dp,0x3f,sizeof(dp));
    for(int i=1;i<=n;++i)
    {
        scanf("%d",&num[i]);
        dp[i][i]=1;
    }
    for(int len=2;len<=n;++len)
    {//枚举区间长度
        for(int l=1;l<=n-len+1;++l)
        {//枚举区间左端点
            int r=l+len-1;
            for(int k=l;k<r;++k)
            {
                dp[l][r]=min(dp[l][r],dp[l][k]+dp[k+1][r]);
            }
            if(num[l]==num[r])
            {
                if(l+1==r){dp[l][r]=1;}
                dp[l][r]=min(dp[l][r],dp[l+1][r-1]);
            }
        }
    }
    printf("%d\n",dp[1][n]);
    return 0;
}

E. Marbles

time limit per test：2 seconds

memory limit per test：256 megabytes

input：standard input

output：standard output

In the spirit of the holidays, Saitama has given Genos two grid paths of length n (a weird gift even by Saitama's standards). A grid path is an ordered sequence of neighbouring squares in an infinite grid. Two squares are neighbouring if they share a side.

One example of a grid path is (0, 0) → (0, 1) → (0, 2) → (1, 2) → (1, 1) → (0, 1) → ( - 1, 1). Note that squares in this sequence might be repeated, i.e. path has self intersections.

Movement within a grid path is restricted to adjacent squares within the sequence. That is, from the i-th square, one can only move to the (i - 1)-th or (i + 1)-th squares of this path. Note that there is only a single valid move from the first and last squares of a grid path. Also note, that even if there is some j-th square of the path that coincides with the i-th square, only moves to (i - 1)-th and (i + 1)-th squares are available. For example, from the second square in the above sequence, one can only move to either the first or third squares.

To ensure that movement is not ambiguous, the two grid paths will not have an alternating sequence of three squares. For example, a contiguous subsequence (0, 0) → (0, 1) → (0, 0) cannot occur in a valid grid path.

One marble is placed on the first square of each grid path. Genos wants to get both marbles to the last square of each grid path. However, there is a catch. Whenever he moves one marble, the other marble will copy its movement if possible. For instance, if one marble moves east, then the other marble will try and move east as well. By try, we mean if moving east is a valid move, then the marble will move east.

Moving north increases the second coordinate by 1, while moving south decreases it by 1. Similarly, moving east increases first coordinate by 1, while moving west decreases it.

Given these two valid grid paths, Genos wants to know if it is possible to move both marbles to the ends of their respective paths. That is, if it is possible to move the marbles such that both marbles rest on the last square of their respective paths.

Input

The first line of the input contains a single integer n (2 ≤ n ≤ 1 000 000) — the length of the paths.

The second line of the input contains a string consisting of n - 1 characters (each of which is either 'N', 'E', 'S', or 'W') — the first grid path. The characters can be thought of as the sequence of moves needed to traverse the grid path. For example, the example path in the problem statement can be expressed by the string "NNESWW".

The third line of the input contains a string of n - 1 characters (each of which is either 'N', 'E', 'S', or 'W') — the second grid path.

Output

Print "YES" (without quotes) if it is possible for both marbles to be at the end position at the same time. Print "NO" (without quotes) otherwise. In both cases, the answer is case-insensitive.

Examples

Input

7
NNESWW
SWSWSW

Output

YES

Input

3
NN
SS

Output

NO

Note

In the first sample, the first grid path is the one described in the statement. Moreover, the following sequence of moves will get both marbles to the end: NNESWWSWSW.

In the second sample, no sequence of moves can get both marbles to the end.

题目链接：http://codeforces.com/contest/608/problem/E

分析：先贴代码，用reverse做！

下面给出AC代码：

#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=1000005;
int n;
char s1[maxn],s2[maxn];
int main(){
    scanf("%d%s%s",&n,s1+1,s2+1);
    reverse(s1+1,s1+n);
    for(int i=1;i<n;++i)
    {
        if(s1[i]=='N')s1[i]='S';
        else if(s1[i]=='S')s1[i]='N';
        else if(s1[i]=='W')s1[i]='E';
        else s1[i]='W';
    }
    unsigned long long h1=0,h2=0,fa=1;
    for(int i=1;i<n;++i)
    {
        h1=h1+s1[i]*fa;
        h2=h2*233u+s2[n-i];
        fa*=233u;
        if(h1==h2)return puts("NO"),0;
    }
    puts("YES");
    return 0;
}