浅谈数据结构之主席树(线段树进阶版)

今天看了点主席树的概念，加上飞哥上次讲的，目前对主席树有了大致的了解，简单谈谈吧，不讲代码，只讲思路，日后贴题！

      Orz高级数据结构发明者主席！！最早在CLJ的课件里第一次看到了这个词，最近做区间第K大时又想起了这茬，这方面资料也挺少的，于是再次膜拜下主席,对主席树理解有不到位的地方也欢迎指正。

 

然后读以下文字时最好有些线段树的预备知识，毕竟根据发明者的原话：“想法是对原序列的每一个前缀[1..i]建立出一颗线段树维护值域上每个数的出现次数，然后发现这样的树是可以减的，然后就没有然后了”

主席树可以用来解决如下问题：“给出一列数,a1,a2…an,每次询问其中连续的一段区间ai到aj其中的第K大的数是多少？”

建那么多的线段树显然会MLE！！但是为了便于理解，这里先把这个岔放下。我们先新开一个数组t[n]，其中存着an排序并去重的值。

那么每棵线段树维护的内容是什么呢？是a1到ai这段区间中的数在t[n]中出现的次数。这段话的内容也许有点抽象，举个例子 an：4 1 1 2 8 9 4 4 3

排序并去重后得到{tn}

tn：1 2 3 4 8 9

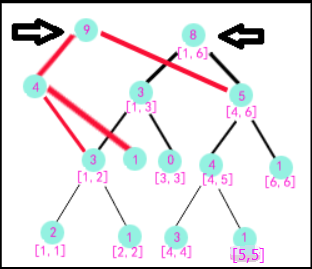
下面对前缀a[1..9]建树，它有两个1,一个2,一个3，三个4，一个8和一个9，那么它的出现次数便是线段树维护的值（为表示清楚记为Cn）建树完后如下图，树中每个节点的值表示t[i,j]中的数字在a[1..9]中出现的次数和，i，j即为节点下面标出的区间。

下面我们来看对于这棵树如何求第K大值。比如我们求a[1..9]中第6大的数是多少？我们看到根节点的左儿子只有4个元素，那么第6大数一定在右儿子中，并且我们可以把问题递归下去即求区间t[4,6]的三个数中为a[1..9]去除所有数字为t[1],t[2],t[3]后第2大的数是多少。（c[1]+c[2]+c[3]=4，那么6-4=2）。我们看到此时的左儿子（区间t[4,5]）有4个元素，4>2,因此第二大数一定在左儿子中，递归进入左儿子，此时即求区间t[4,5]的两个数中

为a[1..9]去除所有数字为t[1],t[2],t[3],t[6]后第2大的数是多少。最后区间[4,4]有三个元素，3>2，所以第二大数一定在区间[4,4]里即t[4]=4，所以a[1..9]中第6大数为4。

这里要记住的是对于每个i , a[1,i]都有一棵树，求a[L,R]的第K大与求a[1,R]的类似，只要在每层递归时减去a[1，L-1]所在树的相应部分即可，比如在a[L,R]，小于t[mid]的数有6个，在a[1,L-1] 小于t[mid]的数有2个，那么在a[L,R] 小于t[mid]的数就有6-2=4个，递归过程和上面类似，不再详细展开。

下面解决MLE这个梗。如下图画出a1…5到9为前缀的树，然后发现树的形态都非常像！！

 

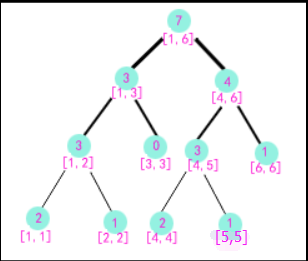
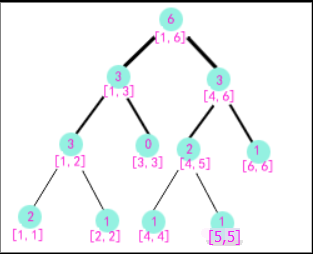
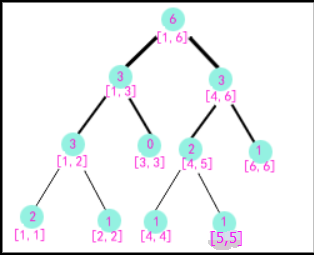
这是我们能够压缩的空间。例如以a[1..9]为前缀建的树的右子树与以a[1..8]为前缀建的树的右子树是相同的！！因此在建树a[1..9]的时候（建树是从1到9的顺序）根节点可以直接向a[1..8]的右子树连一条边。同理，对于根节点的左儿子来说（现在把这个点看做根节点），它的左子树和a[1..8]的相应部分也是相同的，因此也连一条边，如下图所示

 

这样我们只增加了三个点却保存了两棵树的所有信息！！像这样在前面树的基础上建树，我们只需要开一个数组储存图示两个箭头所指的根的位置就够了，顺着根向下遍历便是如前所述一棵完整的线段树