后缀数组(一堆干货)

其实就是将两篇论文里的东西整合在了一起，并且提供了一个比较好理解的板。

 

后缀数组

 

        字符串：一个字符串S是将n个字符顺次排列形成的数组，n称为S的长度，表示为len(S)。S的第i个字符表示为S[i]。

        子串：字符串S的子串S[i…j]，i<=j，表示从S串中从i到j这一段，也就是顺次排列S[i]，S[i+1]，……，S[j]形成的字符串。

        后缀：后缀是指从某个位置i开始到整个字符串末尾结束的一个特殊子串。字符串S的从i开关的后缀表示为Suffix(S,i)，也就是Suffix(S,i)=S[i…len(S)]。

 

        关于字符串的大小比较，是指通常所说的“字典顺序”比较，也就是对于两个字符串u、v，令i从1开始顺次比较u[i]和v[i]，如果u[i]＝v[i]则令i加1，否则若u[i]<v[i]则认为u<v，u[i]>v[i]则认为u>v（也就是v<u），比较结束。如果i>len(u)或者i>len(v)仍未比较结果，那么若len(u)<len(v)则认为u<v，若len(u)=len(v)则认为u=v，若len(u)>len(v)则u>v。

        从字符串的大小比较定义来看，S的开头两个位置后缀u和v进行比较的结果不可能是相等，因为u=v的必要条件len(u)=len(v)是不可能满足的。

        对于约定的字符串S，从位置i开头的后缀直接写成Suffix(i)，省去参数S。

 

        后缀数组：后缀数组SA是一个一维数组，它保存1..n的某个排列SA[1]，SA[2]，……，SA[n]，并保证Suffix(SA[i])<Suffix(SA[i+1])，1<=i<n。也就是将S的n个后缀从小到大进行排序之后把排好序的后缀的开头位置顺次放入SA中。

        名次数组：名次数组Rank[i]表示在字符串S中以i开始后缀在所有的后缀中排名第几。

        简单地说，后缀数组是“排第几的是谁？”，名次数组是“你排第几？”。容易看出后缀数组和名次数组互为逆运算。

 

下面仅介绍倍增法构造后缀数组

         最直接的方法，当然是把S的后缀都看作一些普通的字符串，按照一般字符串排序的方法对它们从小到大进行排序。

         不难看出这样的方法是很笨拙的，因为它没有利用各个后缀之间的有机联系，所以它的效率不高。倍增算法正是充分利用了各个后缀之间的联系，将构造后缀数组的数组的最坏时间复杂度成功降到O(nlogn)。

         对于一个字符串u，我们定义u的k－前缀

         定义k－前缀比较关系<k、=k和<=k：

         设两个字符串u和v，

                u<kv 当且仅当uk<vk

                u=kv 当且仅当uk=vk

                u≤kv 当且仅当uk≤vk

        直观地看这些加了一个下标k的比较符号的意义就是对两个字符串的前k个字符进行字典序比较，特别的一点就是在作大于和小于的比较时如果某个字符串的长度达不到k也没有关系，只要能够在k个字符比较结束之前得到第一个字符串小于第二个字符串就可以了。

        根据前缀比较符的性质我们可以得到以下的非常重要的性质：

                性质1.1 对于k>n，Suffix(i)<kSuffix(j)等价于 Suffix(i)<Suffix(j)。

                性质1.2 Suffix(i)=2kSuffix(j)等价于

                        Suffix(i)=kSuffix(j)且Suffix(i+k)=kSuffix(j+k)。

                性质1.3 Suffix(i)<2kSuffix(j)等价于

                        Suffix(i)<kSuffix(j)或（Suffix(i)=kSuffix(j)且Suffix(i+k)<kSuffix(j+k)）。

        这里有一个问题，当i+k>n或者j+k>n的时候Suffix(i+k)或者Suffix(j+k)是无明确定义的表达式，所以我们在字符串S的末尾添加一个’$’特殊符号，让它比字符串中所有的字符都小，这样即可以满足字典序比较的要求，也能不越界。

 

        基于上面的结论，倍增算法的主要思路是：用倍增的方法对每个字符开始的长度为2^k的子字符串进行排序，求出排名，即rank值。k从0开始，每次加1，当2^k大于n以后，每个字符开始的长度为2^k的子字符串便相当于所有的后缀。并且这些子字符串一定已经比较出大小，即Rank值中没有相同的值，那么此时的Rank值就是最后的结果。每一次排序都利用上次长度为2^k-1的字符串Rank值，那么长度为2^k的字符串就可以用两个长度为2^k-1的字符串的排名作为关键字表示，然后进行基数排序，便得出了长度为2^k的字符串的rank值。以字符串“aabaaaab”为例，整个过程如图2所示。其中x、y是表示长度为2^k的字符串的两个关键字。第一趟排序x是直接将字符串转化成数字，y直接赋值为0。

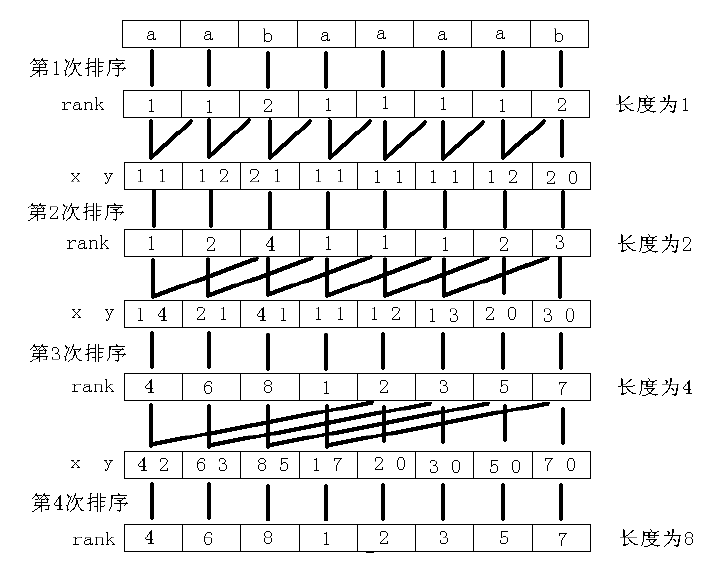
最长公共前缀

         现在一个字符串S的后缀数组SA可以在O(nlogn)的时候内计算出来。利用SA我们已经可以做很多事情，比如在O(mlogn)的时间内进行模式匹配，其中m，n分别为模式串和待匹配串的长度。但是要想更充分地发挥后缀数组的威力，我们还需要计算一个辅助的工具――最长公共前缀（Longest Common Prefix）。

         对于两个字符串u，v定义函数lcp(u,v)=max(i|u=iv)，也就是从头开始顺次比较u和v的对应字符，对应字符持续相等的最大位置，称为这两个字符串的最长公共前缀。

         对正整数i，j定义LCP(i,j)=lcp(Suffix(SA[i]),Suffix(SA[j])，其中i，j均为1到n的整数。LCPi(I,j)也就是后缀数组中第i个和第j个后缀的最长公共前缀的长度。

         关于LCP有两个显而易见的性质：

                  性质1     LCP(i,j)=LCP(j,i)

                  性质2      LCP(i,i)=len(Suffix(SA[i]))=n-SA[i]+1

         这两个性质的用处在于，我们计算LCP(i,j)时只需要考虑i<j的情况，因为i>j时可交换I,j，i=j时可以直接输出结果n-SA[i]+1。

         直接根据定义，用顺次比较对应字符的方法来计算LCP(I,j)显然是很低效的，时间复杂度为O(n)，所以我们必须进行适当的预处理以降低每次计算LCP的复杂度。

         经过仔细的分析，我们发现LCP函数有一个非常好的性质：

                   设i<j，则LCP(i,j)=min{LCP(k-1,k)|i+1<=k<=j}         （LCP Theorem）  

         要证明LCPTheorem，首先证明 LCP Lemma：

                   对任意1<=i<j<k<=n，LCP(I,k)=min{LCP(I,j),LCP(j,k)}

         证明：设p=min{LCP(I,j),LCP(j,k)}，则有LCP(I,j)>=p,LCP(j,k)>=p。

                   设Suffix(SA[i])=u，Suffix(SA[j])=v，Suffix(SA[k])=w。

                   由u=LCP(I,j)v得u=pv；同理v=pw。

                   于是Suffix(SA[i])=pSuffix(SA[k])，即LCP(I,k)>=p。         （1）

                   又设LCP(I,k)=q>p，则

                   U[1]=w[1],u[2]=w[2],…,u[q]=w[q]。

                   而min{LCP(I,j),LCP(j,k)}=p，说明u[p+1]!=v[p+1]或v[p+1]!=w[q+1]

                   设u[p+1]=x，v[p+1]=y，w[p+1]=z，显然为x<=y<=z，又由p<q得p+1<q，应该有x=z，也就是x=y=z，这与u[p+1]!=v[p+1]或v[p+1]!=w[q+1]矛盾。

                   于是，q>p不成立，即LCP(I,k)<=p。                              （2）

                   综合（1）（2）知LCP(I,k)=p=min{LCP(I,j),LCP(j,k)}，LCP Lemma得证。

         根据数学归纳法可证得，LCPTheorem成立。

 

         定义一维数组height，令;height[i]=LCP(i-1,i)，1<i<=n，并设height[1]=0。

         由LCP Theorem，LCP(I,j)=min{height[k]|i+1<=k<=j}，也就是说，计算LCP(I,j)等同于询问一维数组height中下标在i+1到j范围内的所有元素的最小值。如果height数组是固定的，这就是非常经典的RMQ(Range Minimum Query)问题。

         对于一个固定字符串S，其height数组显然是固定的，只要我们能高效地求出height数组，那么运用RMQ方法进行预处理之后，每次计算LCP(I,j)的时间复杂度就是常数级了。于是只有一个问题了――如果尽量高效地算出height数组。

         根据计算后缀数组的经验，我们不应该把n个后缀看成互不相关的普通字符串，而应该尽量利用它们之间的联系，下面证明一个非常有用的性质：

         为了描述方便，设h[i]=height[Rank[i]]，即height[i]=h[SA[i]]。h数组满足一个性质：

         性质3      对于i>1且Rank[i]>1，一定有h[i]>=h[i-1]-1。

         为了证明性质3，我们有必要明确两个事实：

         设i<n，j<n，Suffix(i)和Suffix(j)满足lcp(Suffix(i),Suffix(j))>1，则以下两点成立：

         Fact1 Suffix(i)<Suffix(j) 等价于 ;Suffix(i+1)<Suffix(j+1)。

         Fact2 一定有lcp(Suffix(i+1),Suffix(j+1))=lcp(Suffix(i),Suffix(j))-1。

         看起来很神奇，但其实很自然：lcp(Suffix(i),Suffix(j))>1说明Suffix(i)和Suffix(j)的第一个字符是相同的，设它为a，则Suffix(i)相当于a后连接Suffix(i+1)，Suffix(j)相当于a后连接Suffix(j+1)。比较Suffix(i)和Suffix(j)时，第一个字符一定是相等的，于是后面就等价比较Suffix(i)和Suffix(j)，因此Fact 1成立。Fact 2可类似证明。

 

         于是可以证明性质3：

         当h[i-1]<=1时，结论显然成立，因h[i]>=0>=h[i-1]-1。

         当h[i-1]>1时，也即height[Rank[i-1]]>1，可见Rank[i-1]>1，因height[1]=0。

         令j=i-1，k=SA[Rank[j]-1]。显然有Suffix(k)<Suffix(j)。

         根据h[i-1]=lcp(Suffix(k),Suffix(j))>1和Suffix(k)<Suffix(j)。

         由Fact 2 知lcp(Suffix(k+1),Suffix(i))=h[i-1]-1。

         由Fact 1 知Rank[k+1]<Rank[i]，也就是Rank[k+1]<=Rank[i]-1。

         于是根据LCPCorollary，有

         LCP(Rank[i]-1,Rank[i])>=LCP(Rank[k+1],Rank[i])

                                               =lcp(Suffix(k+1),Suffix(i))

                                               =h[i-1]-1

         由于h[i]=height[Rank[i]]=LCP(Rank[i]-1,Rank[i])，最终得到h[i]>=h[i-1]-1。

        

         根据性质3，可以令i从1循环到n按照如下方法依次算了h[i]：

         若Rank[i]=1，则h[i]=0。字符比较次数为0.

         若i=1或者h[i-1]<=1，则直接将Suffix(i)和Suffix(Rank[i]-1)从第一个字符开始依次比较直到有字符不同，由此算出h[i]。字符比较次数为h[i]+1，不超过h[i]-h[i-1]+2。

         否则，说明i>1，Rank[i]>1，h[i-1]>1，根据性质3，Suffix(i)和Suffix(Rank[i]-1)至少有前h[i-1]-1个字符是相同的，于是字符比较可以从h[i-1]开始，直到某个字符不相同，由此计算出h[i]。字符比较次数为h[i]-h[i-1]+2。

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 using namespace std;
 5 const int N=21000;
 6 struct SuffixArray
 7 {
 8     int n,len,A[N],C[N],sa[N],rank[N],height[N];
 9     struct RadixEle
10     {
11         int id,k[2];
12         RadixEle(){}
13         RadixEle(int a,int b,int c){id=a;k[0]=b;k[1]=c;}
14     }RT[N],RE[N];
15     void RadixSort()
16     {
17         for(int y=1;y>=0;y--)
18         {
19             memset(C,0,sizeof(C));
20             for(int i=1;i<=n;i++) C[RE[i].k[y]]++;
21             for(int i=1;i<N;i++) C[i]+=C[i-1];
22             for(int i=n;i>=1;i--) RT[C[RE[i].k[y]]--]=RE[i];
23             for(int i=1;i<=n;i++) RE[i]=RT[i];
24         }
25         for(int i=1;i<=n;i++)
26         {
27             rank[RE[i].id]=rank[RE[i-1].id];
28             if(RE[i].k[0]!=RE[i-1].k[0]||RE[i].k[1]!=RE[i-1].k[1])
29                 rank[RE[i].id]++;
30         }
31     }
32     void CalcSA()
33     {
34         for(int i=1;i<=n;i++) RE[i]=RadixEle(i,A[i],0);
35         RadixSort();
36         for(int k=1;1+k<=n;k*=2)
37         {
38             for(int i=1;i<=n;i++) 
39                 RE[i]=RadixEle(i,rank[i],(i+k<=n?rank[i+k]:0));
40             RadixSort();
41         }
42         for(int i=1;i<=n;i++) sa[rank[i]]=i;
43     }
44     void CalcHeight()
45     {
46         int h=0;
47         for(int i=1;i<=n;i++)
48         {
49             if(rank[i]==1) h=0;
50             else
51             {
52                 int k=sa[rank[i]-1];
53                 if(--h<0) h=0;
54                 while(A[i+h]==A[k+h]) h++;
55             }
56             height[rank[i]]=h;
57         }
58     }
59 }SA;

 

posted @ 2017-03-25 22:46  Angel_Kitty  阅读(2352)  评论(3)  编辑  收藏  举报