从零开始学建树(树的分治，树的重心)

分治算法在树的路径问题中的应用

一、树的分治算法

树的分治算法是分治思想在树型结构上的体现。

任一个具有n个节点的连通路，它的任何一棵树的树枝数为n-1

分治：除去树中的某些对象，使原树被分解成若干互不相交的部分。

分治算法分为两种：一种是点的分治，一种是边的分治

1.基于点的分治

1.选取一个点将无根树转为有根树

2.递归处理每一颗以根结点的儿子为根的子树

2.基于边的分治

1.在树中选取一条边

2. 将原有的树分成两棵不相交的树，递归处理。

可以证明在基于点的分治中，如果每次都选取树的重心，那么至多递归
O(LogN)次。

基于边的分治最坏情况下递归次数为O(N)。

二、树的重心

我们选取一个点，要求将其删去后，结点最多的树的结点个数最小，这个点被称作”树的重心”

下面给出一个定理：

存在一个点使得分出的子树的结点个数均不大于N/2

证明：(反证法证明)

 

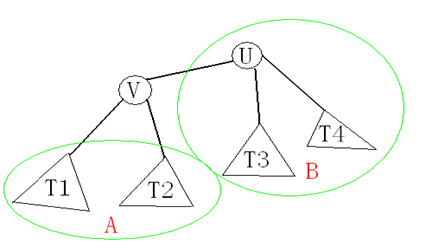
假设U是树的重心，记Size(X)表示以X为根的子树的结点个数。记V为U的儿子中Size值最大的点。

假设Size(V)>N/2，那么我们考虑V作为根结点的情况，记Size’(X)表示此时以X为根的子树的结点个数。

如图。

    对于A部分，显然Size’(Ti)<Size(V)

    对于B部分，Size’(U) = N-Size(V)<Size(V)

    这与树的重心定义矛盾。

    定理得证。

//日后将会给出一些例题去运用以上的结论

转载请注明：http://www.cnblogs.com/ECJTUACM-873284962/