从零基础学三分查找

转载请注明：http://www.cnblogs.com/ECJTUACM-873284962/

今晚是我们学长第二次讲课，讲了一个三分！认真听了一下，感觉不是很难，可能会比二分还简单些！我就把上课讲的内容归纳为一篇文章概述吧！以后也会重点讲解的！

简单点说二分是查找区间，相当于一次函数，三分就是二次函数了，求它的极值，怎么做，数学常用的是求导，计算机就用查找咯，那么请看下面的简单概述吧！

一. 概念

在二分查找的基础上，在右区间（或左区间）再进行一次二分，这样的查找算法称为三分查找，也就是三分法。
三分查找通常用来迅速确定最值。
二分查找所面向的搜索序列的要求是：具有单调性（不一定严格单调）；没有单调性的序列不是使用二分查找。
与二分查找不同的是，三分法所面向的搜索序列的要求是：序列为一个凸性函数。通俗来讲，就是该序列必须有一个最大值（或最小值），在最大值（最小值）的左侧序列，必须满足不严格单调递增（递减），右侧序列必须满足不严格单调递减（递增）。如下图，表示一个有最大值的凸性函数：

二、算法过程

（1）、与二分法类似，先取整个区间的中间值mid。
  
mid = (left + right) / 2;

 

（2）、再取右侧区间的中间值midmid，从而把区间分为三个小区间。
 
midmid = (mid + right) / 2;

 

（3）、我们mid比midmid更靠近最值，我们就舍弃右区间，否则我们舍弃左区间？。
比较mid与midmid谁最靠近最值，只需要确定mid所在的函数值与midmid所在的函数值的大小。当最值为最大值时，mid与midmid中较大的那个自然更为靠近最值。最值为最小值时同理。 
if (cal(mid) > cal(midmid))  
     right = midmid;  
else  
      left = mid;
（4）、重复（1）（2）（3）直至找到最值。
（5）、另一种三分写法
 1 double three_devide(double low,double up)
 2 {
 3     double m1,m2;
 4     while(up-low>=eps)
 5     {
 6         m1=low+(up-low)/3;
 7         m2=up-(up-low)/3;
 8         if(f(m1)<=f(m2))
 9             low=m1;
10         else
11             up=m2;
12     }
13     return (m1+m2)/2;
14 }
算法的正确性：
1、mid与midmid在最值的同一侧。由于凸性函数在最大值（最小值）任意一侧都具有单调性，因此，mid与midmid中，更大（小）的那个 数自然更为靠近最值。此时，我们远离最值的那个区间不可能包含最值，因此可以舍弃。
2、mid与midmid在最值的两侧。由于最值在中间的一个区间，因此我们舍弃一个区间后，并不会影响到最值
 1 const double EPS = 1e-10;
 2 double calc(double x)
 3 {
 4     // f(x) = -(x-3)^2 + 2;
 5     return -(x-3.0)*(x-3.0) + 2;
 6 }
 7 
 8 double ternarySearch(double low, double high)
 9 {
10     double mid, midmid;
11     while (low + EPS < high)
12     {
13         mid = (low + high) / 2;
14         midmid = (mid + high) / 2;
15         double mid_value = calc(mid);
16         double midmid_value = calc(midmid);
17         if (mid_value > midmid_value)
18             high = midmid;
19         else
20             low = mid;
21     }
22     return low;
23 }

调用ternarySearch(0, 6)，返回的结果为3.0000

我们都知道 二分查找 适用于单调函数中逼近求解某点的值。

如果遇到凸性或凹形函数时，可以用三分查找求那个凸点或凹点。

下面的方法应该是三分查找的一个变形。

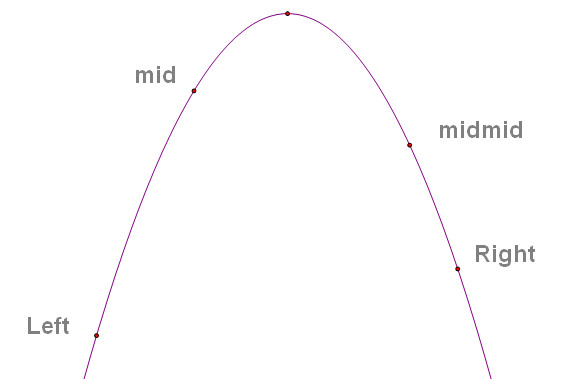
如图所示，已知左右端点L、R，要求找到白点的位置。

思路：通过不断缩小 [L,R] 的范围，无限逼近白点。

做法：先取 [L,R] 的中点 mid，再取 [mid,R] 的中点 mmid，通过比较 f(mid) 与 f(mmid) 的大小来缩小范围。

         当最后 L=R-1 时，再比较下这两个点的值，我们就找到了答案。

1、当 f(mid) > f(mmid) 的时候，我们可以断定 mmid 一定在白点的右边。

反证法：假设 mmid 在白点的左边，则 mid 也一定在白点的左边，又由 f(mid) > f(mmid) 可推出 mmid < mid，与已知矛盾，故假设不成立。

所以，此时可以将 R = mmid 来缩小范围。

2、当 f(mid) < f(mmid) 的时候，我们可以断定 mid 一定在白点的左边。

反证法：假设 mid 在白点的右边，则 mmid 也一定在白点的右边，又由 f(mid) < f(mmid) 可推出 mid > mmid，与已知矛盾，故假设不成立。

同理，此时可以将 L = mid 来缩小范围。

 

 1 int SanFen(int l,int r) //找凸点
 2 {
 3     while(l < r-1)
 4     {
 5         int mid  = (l+r)/2;
 6         int mmid = (mid+r)/2;
 7         if( f(mid) > f(mmid) )
 8             r = mmid;
 9         else
10             l = mid;
11     }
12     return f(l) > f(r) ? l : r;
13 }
 
 日后会以例题的形式进行详细的讲解，这个也就是入门级！
posted @ 2017-03-11 22:11  Angel_Kitty  阅读(4480)  评论(4)  编辑  收藏  举报