hdu 4288 Coder (线段树，区间部分更新)

http://acm.hdu.edu.cn/showproblem.php?pid=4288

题意：

给出三种操作add x 向集合里添加x（这里保证集合中不存在该元素）, del x删除集合里的x（这里保证集合里面不存在x），

sum：

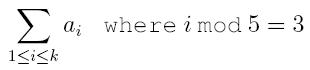
然后给出N个操作，输出每次的sum；

思路：

才开始看到这题就想到了上次那个维护区间（i-a）%k == 0的题目区间部分更新的题目，每个线段树上的节点添加记录该区间内模k余(0到k-1)的值，可是这里是求整个区间，而且一旦删除一个值它们原来满足模k的余数就会发生改变。直接就晕了。。。看了下解题报告原来和上次的题目是类似的，我们还是记录当前区间模5余（0到4）的值，只是稍微进行一下区间合并即可，解题的关键就在于这里的区间合并。当向上更新的时候当前节点的左子树模5余数不变，只要加上就好，而对于右子树由于在该区间的前边又添加len[rt<<1]这些长度的值，所以原来他们模5的余数对于整体的父亲节点来说已经改变了我们只要右子树模5等于i的现在对应于父亲节点为模5等与（len[rt<<1] + i ）%5.然后合并完毕了。。

离散化+离线处理 +区间合并

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <string>

#define CL(a,num) memset((a),(num),sizeof(a))
#define iabs(x)  ((x) > 0 ? (x) : -(x))
#define Min(a,b) (a) > (b)? (b):(a)
#define Max(a,b) (a) > (b)? (a):(b)

#define ll __int64
#define inf 0x7f7f7f7f
#define MOD 100000007
#define lc l,m,rt<<1
#define rc m + 1,r,rt<<1|1
#define pi acos(-1.0)
#define test puts("<------------------->")
#define maxn 10000007
#define M 100007
#define N 100007
using namespace std;
//freopen("din.txt","r",stdin);

ll Mod[N<<2][5];
int len[N<<2];
int val[N],a[N];
char op[N][5];

void pushup(int rt){
    int i;
    len[rt] = len[rt<<1] + len[rt<<1|1];
    //关键理解合并
    for (i = 0; i < 5; ++i) Mod[rt][i] = Mod[rt<<1][i];
    int Lx = len[rt<<1];
    for (i = 0; i < 5; ++i) Mod[rt][(Lx + i)%5] += Mod[rt<<1|1][i];
}
void build(int l,int r,int rt){
    for (int i = 0; i < 5; ++i) Mod[rt][i] = 0;
    len[rt] = 0;
    if (l == r) return ;
    int m = (l + r)>>1;
    build(lc);
    build(rc);
}
void update(int pos,int sc,int l,int r,int rt){
    if (l == r){
        len[rt] += sc;
        Mod[rt][1] += sc*a[l];//对于一个叶子节点来说区间是[1,1]所以模5等于1
        return ;
    }
    int m = (l + r)>>1;
    if (pos <= m) update(pos,sc,lc);
    else update(pos,sc,rc);
    pushup(rt);
}
int bSearch(int L,int R,int v){
    int l = L;
    int r = R;
    while (l <= r){
        int m = (l + r)>>1;
        if (a[m] == v) return m;
        else if (v < a[m]) r = m - 1;
        else l = m + 1;
    }
    return -1;
}
int main(){
    //freopen("din.txt","r",stdin);
    int i,n;
    while (~scanf("%d",&n)){
        int ct = 0;
        for (i = 0; i < n; ++i){
            scanf("%s",op[i]);
            if (op[i][0] != 's'){
                scanf("%d",&val[i]);
                a[++ct] = val[i];
            }
        }
        //离散化
        sort(a + 1,a + 1 + ct);
        int nn = 1;
        for (i = 2; i <= ct; ++i){
            if (a[i] != a[i - 1]) a[++nn] = a[i];
        }
        //离线处理
        build(1,nn,1);
        for (i = 0; i < n; ++i){
            if (op[i][0] == 'a') update(bSearch(1,nn,val[i]),1,1,nn,1);
            else if (op[i][0] == 'd') update(bSearch(1,nn,val[i]),-1,1,nn,1);
            else printf("%I64d\n",Mod[1][3]);
        }
    }
    return 0;
}