pku 3687 Labeling Balls 拓扑排序

http://poj.org/problem?id=3687

本人强烈推荐这道题。。。

才开始自己理解错了题意，以为单纯的利用优先队列每次从入度为0的队列中选出编号最小的点即可，样例过了可是无限WA最后看了看解题报告，原来我理解错了。要求序列小的要尽量靠前，而且输出的不是得到的序列，而是根据序列得到的重量。。

 

很不错的解题报告，本人转载：

在基本的拓扑排序的基础上又增加了一个要求：编号最小的节点要尽量排在前面；在满足上一个条件的基础上，编号第二小的节点要尽量排在前面；在满足前两个条件的基础上，编号第三小的节点要尽量排在前面……依此类推。（注意，这和字典序是两回事，不可以混淆。）

如图 1 所示，满足要求的拓扑序应该是：6 4 1 3 9 2 5 7 8 0。

 

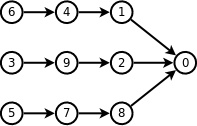
图 1 一个拓扑排序的例子

一般来说，在一个有向无环图中，用 BFS 进行拓扑排序是比较常见的做法，如算法 1 所示。但是它不一定能得到本题要求的拓扑序。

1. 把所有入度为 0 的节点放进队列 Q

2. WHILE： Q 不是空队列

3.     从 Q 中取出队列首元素 a，把 a 添加到答案的尾部。

4.     FOR：所有从 a 出发的边 a → b

5.         把 b 的入度减 1。如果 b 的入度变为 0，则把 b 放进队列 Q。

算法 1 用 BFS 进行拓扑排序

为了解决本问题，下面让我来探究一下拓扑序的一些性质。以图 1 为例，节点 0 毫无疑问排在最后。除了节点 0 以外，有三条互相平行的路径：6 → 4 → 1、 3 → 9 → 2 和 5 → 7→ 8。一条路径上的各个节点的先后关系都是不能改变的，比如路径 6 → 4 → 1 上的三个节点在拓扑序中，一定是 6 在最前，1 在最后。但是，互相平行的各条路径，在总的拓扑序中任意交错都是合法的。比如，以下都是图 1 的合法拓扑序：

6 4 1 3 9 2 5 7 8 0、 3 6 9 4 5 1 7 8 2 0、 5 6 4 7 3 8 1 9 2 0、 3 5 6 4 1 7 9 2 8 0、 6 5 7 8 4 3 9 2 1 0。

怎么才能找出题目要求的拓扑序呢？在这里，我想用字典序最先的拓扑序来引出这个算法。算法 2 可以求出字典序最先的拓扑序。

1. 把所有入度为 0 的节点放进优先队列 PQ

2. WHILE： PQ 不是空队列

3.     从 PQ 中取出编号最小的元素 a，把 a 添加到答案的尾部。

4.     FOR：所有从 a 出发的边 a → b

5.        把 b 的入度减 1。如果 b 的入度变为 0，则把 b 放进优先队列PQ。

算法 2 求出字典序最先的拓扑序

可见，算法 2 和算法 1 基本一样，只是把队列改成了优先队列。用它求出的图 1 的字典序最先的拓扑序为：3 5 6 4 1 7 8 9 2 0。但是这显然不是本题要求的答案，因为节点 1 的位置还不够靠前。

算法 2 可以算是一个贪心算法，每一步都找编号最小的节点。但是对于图 1 中的三条路径，头的编号比较小的，不一定要先出队列。正确的步骤应该如下：

1. 节点 0 的位置是铁定在最后的，不用考虑。只考虑剩下的三条路径。
2. 先找编号最小的，节点 1。把它和它所在的路径中位于它前面的节点全部拿出来。目前的答案是 6 4 1，这样， 节点 1 就尽量靠前了。
3. 再找剩下的节点中编号最小的，节点 2。把它和它所在的路径中位于它前面的节点全部拿出来。目前的答案是 6 4 1 3 9 2 ，这样，节点 2 就尽量靠前了。
4. 只剩下一条路径了，只能依次把其中的节点拿出来。最后答案就是 6 4 1 3 9 2 5 7 8 0。

显然，算法 2 的贪心策略对于这个问题是不可行的。不能着眼于每条路径的头，而是要找编号最小的节点在哪条路径上，优先把这条路径拿出来。但问题在于，在 BFS 的过程中，我们只能看到每条路径的头，看不到后面的节点，这该怎么办呢？

让我们换个角度想一想，节点 3 和 6，应该是 6 先出队列，因为节点 1 在 6 的后面。这和节点 3 和 6 的编号大小没有任何关系。但是，再看另外两条路径的尾部，节点 2 和 8，可以肯定地说，2 一定先出队列，因为它们后面都没有别的节点了，这个时候完全以这两个节点本身的编号大小决定顺序。归纳起来就是说，对于若干条平行的路径，小的头部不一定排在前面，但是大的尾部一定排在后面。于是，就有了算法 3。

1. 把所有出度为 0 的节点放进优先队列 PQ
2. WHILE： PQ 不是空队列
3.     从 PQ 中取出编号最大的元素 a，把 a 添加到答案的头部。
4.     FOR：所有指向 a 的边 b → a
5.        把 b 的出度减 1。如果 b 的出度变为 0，则把 b 放进优先队列PQ。

算法 3 求出本题目要求的拓扑序

 

自己的代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#define maxn 207
using namespace std;

int f[maxn],ind[maxn],map[maxn][maxn];
int arry[maxn];
int n,m;

struct cmp
{
    bool operator ()(int &a,int &b)
    {
        return a < b;
    }
};
void init()
{
    int i,j;
    for (i = 0; i <= n; ++i)
    {
        ind[i] = 0; f[i] = i;
        for (j = 0; j <= n; ++j)
        map[i][j] = 0;
    }
}
int find(int x)
{
    if (x != f[x])
    f[x] = find(f[x]);
    return f[x];
}
int main()
{
    //freopen("d.txt","r",stdin);
    int t,i,a,b;
    cin>>t;
    while (t--)
    {
        bool flag = false;
        cin>>n>>m;
        init();
        for (i = 0; i < m; ++i)
        {
            cin>>a>>b;
            if (map[b][a]) continue;
            map[b][a] = 1;
            int c = find(a);
            int d = find(b);
            //printf("%d %d %d %d\n",a,b,c,d);
            if (!flag && c != d)
            {
                ind[a]++;
                f[d] = c;
            }
            else
            {
                flag = true;
            }
        }
        if (flag) printf("-1\n");
        else
        {
            priority_queue< int, vector<int>,cmp>q;
            while (!q.empty()) q.pop();
            for (i = 1; i <= n; ++i)
            {
                if (ind[i] == 0)
                {
                    q.push(i);
                    ind[i] = -1;
                }
            }
            int ct = n;
            while (!q.empty())
            {
                int tmp = q.top(); q.pop();
                arry[tmp] = ct--;
                for (i = 1; i <= n; ++i)
                {
                    if (map[tmp][i])
                    {
                        ind[i]--;
                        if (ind[i] == 0)
                        {
                            ind[i] = -1;
                            q.push(i);
                        }
                    }
                }
            }
            for (i = 1; i < n; ++i)
            printf("%d ",arry[i]);
            printf("%d\n",arry[n]);
        }
    }
    return 0;
}