LeetCode Android Unlock Patterns

原题链接在这里：https://leetcode.com/problems/android-unlock-patterns/description/

题目：

Given an Android 3x3 key lock screen and two integers m and n, where 1 ≤ m ≤ n ≤ 9, count the total number of unlock patterns of the Android lock screen, which consist of minimum of m keys and maximum n keys.

Rules for a valid pattern:

1. Each pattern must connect at least m keys and at most n keys.
2. All the keys must be distinct.
3. If the line connecting two consecutive keys in the pattern passes through any other keys, the other keys must have previously selected in the pattern. No jumps through non selected key is allowed.
4. The order of keys used matters.

 

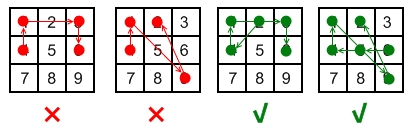
Explanation:

| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |

Invalid move: 4 - 1 - 3 - 6 
Line 1 - 3 passes through key 2 which had not been selected in the pattern.

Invalid move: 4 - 1 - 9 - 2
Line 1 - 9 passes through key 5 which had not been selected in the pattern.

Valid move: 2 - 4 - 1 - 3 - 6
Line 1 - 3 is valid because it passes through key 2, which had been selected in the pattern

Valid move: 6 - 5 - 4 - 1 - 9 - 2
Line 1 - 9 is valid because it passes through key 5, which had been selected in the pattern.

Example:
Given m = 1, n = 1, return 9.

题解：

从当前点cur开始做dfs. 每次remain steps 减一. stop condition 是remain steps为0, 此时只有一种可能, return 1.

在做dfs时需要确保下个数要么相连要么隔着的数已经visit过.

Time Complexity: O(n!). n是maximum pattern length. 共有O(n!)种可能结果.

Space: O(n). stack space.

AC Java:

class Solution {
    public int numberOfPatterns(int m, int n) {
        int [][] skip = new int[10][10];
        skip[1][3] = skip[3][1] = 2;
        skip[1][7] = skip[7][1] = 4;
        skip[3][9] = skip[9][3] = 6;
        skip[7][9] = skip[9][7] = 8;
        skip[1][9] = skip[9][1] = skip[3][7] = skip[7][3] = skip[2][8] = skip[8][2] = skip[4][6] = skip[6][4] = 5;
        
        boolean [] visited = new boolean[10];
        int res = 0;
        for(int i = m; i<=n; i++){
            // 1, 3, 7, 9是symmetric的
            res += dfs(skip, visited, 1, i-1) * 4;
            // 2, 4, 6, 8是symmetric的
            res += dfs(skip, visited, 2, i-1) * 4;
            res += dfs(skip, visited, 5, i-1);
        }
        return res;
    }
    
    private int dfs(int [][] skip, boolean [] visited, int cur, int remain){
        if(remain == 0){
            return 1;
        }
        
        int res = 0;
        visited[cur] = true;
        for(int i = 1; i<=9; i++){
            //如果i没被visited过，并且要么cur和i连着 要么cur和i之间的skip number之前visit 过
            if(!visited[i] && (skip[cur][i]==0 || visited[skip[cur][i]])){
                res += dfs(skip, visited, i, remain-1);
            }
        }
        visited[cur] = false;
        return res;
    }
}