LeetCode 1631. Path With Minimum Effort

原题链接在这里：https://leetcode.com/problems/path-with-minimum-effort/description/

题目：

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

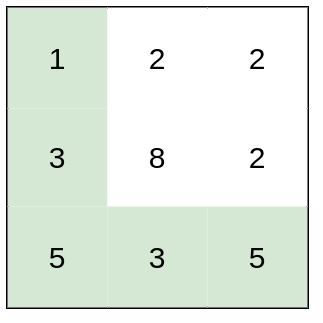
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

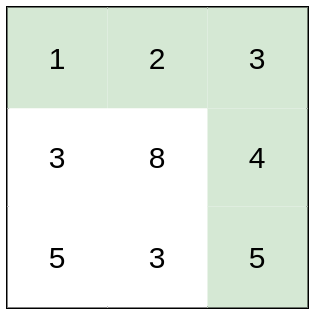
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

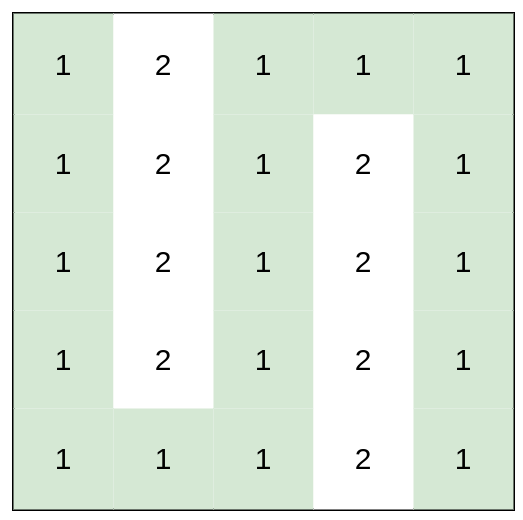
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

Constraints:

• rows == heights.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 106

题解：

Use minHeap to keep track of (x, y, diff), sorted based on diff.

When polling from minHeap, if it reaches the bottom right, then return the diff.

Otherwise, check all four directions and if not visited before, add to minHeap.

Time Complexity: O(m * n * log(m * n)). m = heights.length. n = heights[0].length.

Space: O(m * n).

AC Java:

class Solution {
    int[][] dirs = new int[][]{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    public int minimumEffortPath(int[][] heights) {
        int m = heights.length;
        int n = heights[0].length;

        boolean[][] visited = new boolean[m][n];
        PriorityQueue<int[]> minHeap = new PriorityQueue<>((a, b) -> a[2] - b[2]);
        minHeap.add(new int[]{0, 0, 0});
        while(!minHeap.isEmpty()){
            int[] cur = minHeap.poll();
            if(cur[0] == m - 1 && cur[1] == n - 1){
                return cur[2];
            }

            visited[cur[0]][cur[1]] = true;

            for(int [] dir : dirs){
                int x = cur[0] + dir[0];
                int y = cur[1] + dir[1];
                if(x < 0 || x >= m || y < 0 || y >= n || visited[x][y]){
                    continue;
                }

                int diff = Math.abs(heights[x][y] - heights[cur[0]][cur[1]]);
                minHeap.add(new int[]{x, y, Math.max(cur[2], diff)});
            }
        }

        return 0;
    }
}