LeetCode 2268. Minimum Number of Keypresses
原题链接在这里:https://leetcode.com/problems/minimum-number-of-keypresses/description/
题目:
You have a keypad with 9 buttons, numbered from 1 to 9, each mapped to lowercase English letters. You can choose which characters each button is matched to as long as:
- All 26 lowercase English letters are mapped to.
- Each character is mapped to by exactly
1button. - Each button maps to at most
3characters.
To type the first character matched to a button, you press the button once. To type the second character, you press the button twice, and so on.
Given a string s, return the minimum number of keypresses needed to type s using your keypad.
Note that the characters mapped to by each button, and the order they are mapped in cannot be changed.
Example 1:
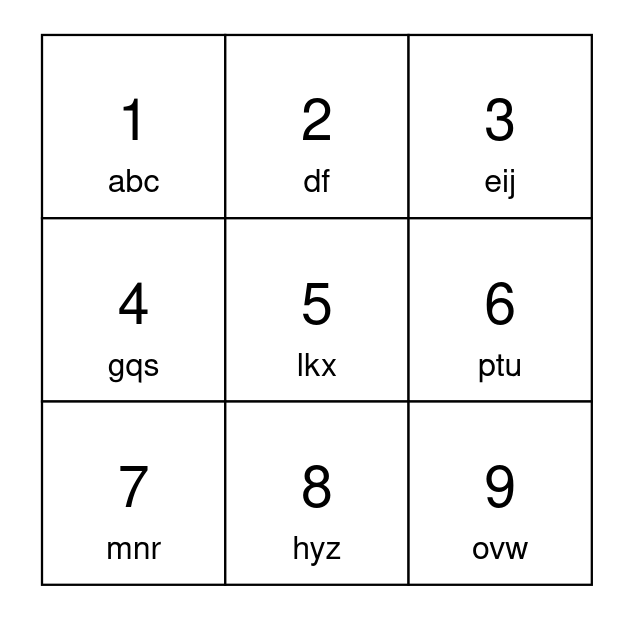
Input: s = "apple" Output: 5 Explanation: One optimal way to setup your keypad is shown above. Type 'a' by pressing button 1 once. Type 'p' by pressing button 6 once. Type 'p' by pressing button 6 once. Type 'l' by pressing button 5 once. Type 'e' by pressing button 3 once. A total of 5 button presses are needed, so return 5.
Example 2:
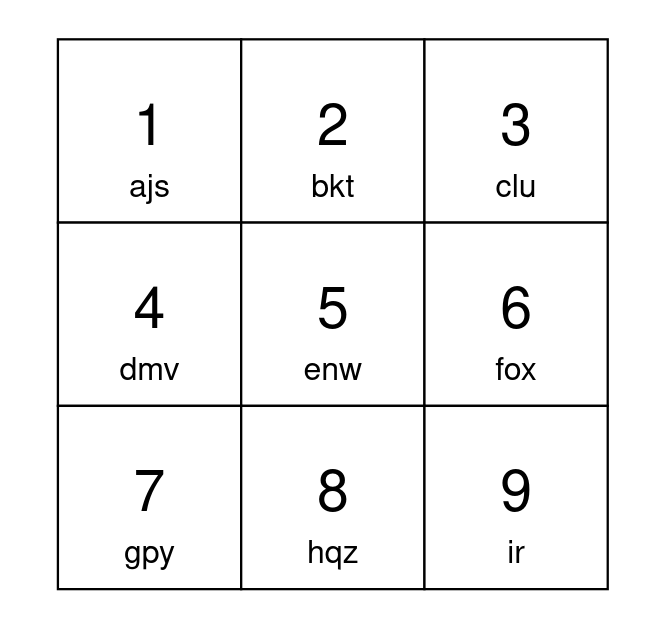
Input: s = "abcdefghijkl" Output: 15 Explanation: One optimal way to setup your keypad is shown above. The letters 'a' to 'i' can each be typed by pressing a button once. Type 'j' by pressing button 1 twice. Type 'k' by pressing button 2 twice. Type 'l' by pressing button 3 twice. A total of 15 button presses are needed, so return 15.
Constraints:
1 <= s.length <= 105sconsists of lowercase English letters.
题解:
Need to put the most frequent chars in the front of each button.
We put the 9 most frequent chars at the beginning of each button.
Then next 9 most frequent chars at the second of each button.
Time Complexity: O(n). n = s.length().
Space: O(1).
AC Java:
1 class Solution { 2 public int minimumKeypresses(String s) { 3 int[] count = new int[26]; 4 for(int i = 0; i < s.length(); i++){ 5 count[s.charAt(i) - 'a']++; 6 } 7 8 Arrays.sort(count); 9 int res = 0; 10 int ind = 0; 11 for(int i = 25; i >= 0; i--){ 12 res += count[i] * (ind / 9 + 1); 13 ind++; 14 } 15 16 return res; 17 } 18 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号