LeetCode 1373. Maximum Sum BST in Binary Tree

原题链接在这里：https://leetcode.com/problems/maximum-sum-bst-in-binary-tree/description/

题目：

Given a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

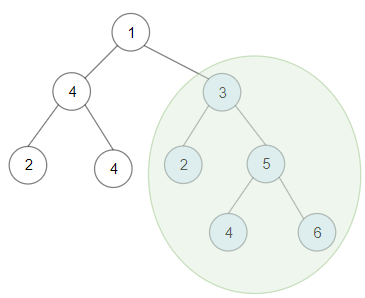
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Example 2:

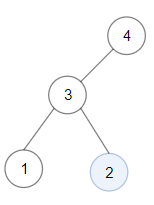
Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Constraints:

• The number of nodes in the tree is in the range [1, 4 * 104].
• -4 * 104 <= Node.val <= 4 * 104

题解：

Bottom up DFS. 

DFS state needs the current root node.

DFS returns an array with subtree min value, max value and sum. If the subtree is not a BST, then return null.

Check both left and right subtrees returned array are not null and rootval val is within (left substree.max, right subtree. min).

If current node could also be a subtree. update the res.

Note: when return current node subtree min and max, it needs to do Math.min(l[0], root.val) and Math.max(r[1], root.val). Since previous l[0] and r[1] could be Integer.MIN_VALUE or Integer.MAX_VALUE.

Time Complexity: O(n). n is number of nodes in the tree.

Space: O(h). The height of the tree.

AC Java:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int res = 0;
    public int maxSumBST(TreeNode root) {
        dfs(root);
        return res;
    }

    private int[] dfs(TreeNode root){
        if(root == null){
            return new int[]{Integer.MAX_VALUE, Integer.MIN_VALUE, 0};
        }

        int[] l = dfs(root.left);
        int[] r = dfs(root.right);
        if(l == null || r == null || root.val <= l[1] || root.val >= r[0]){
            return null;
        }
        
        int total = l[2] + r[2] + root.val;
        res = Math.max(res, total);
        int min = Math.min(l[0], root.val);
        int max = Math.max(r[1], root.val);
        return new int[]{min, max, total};
    }
}

类似Largest BST Subtree.