LeetCode 1340. Jump Game V

原题链接在这里：https://leetcode.com/problems/jump-game-v/description/

题目：

Given an array of integers arr and an integer d. In one step you can jump from index i to index:

• i + x where: i + x < arr.length and  0 < x <= d.
• i - x where: i - x >= 0 and  0 < x <= d.

In addition, you can only jump from index i to index j if arr[i] > arr[j] and arr[i] > arr[k] for all indices k between i and j (More formally min(i, j) < k < max(i, j)).

You can choose any index of the array and start jumping. Return the maximum number of indices you can visit.

Notice that you can not jump outside of the array at any time.

Example 1:

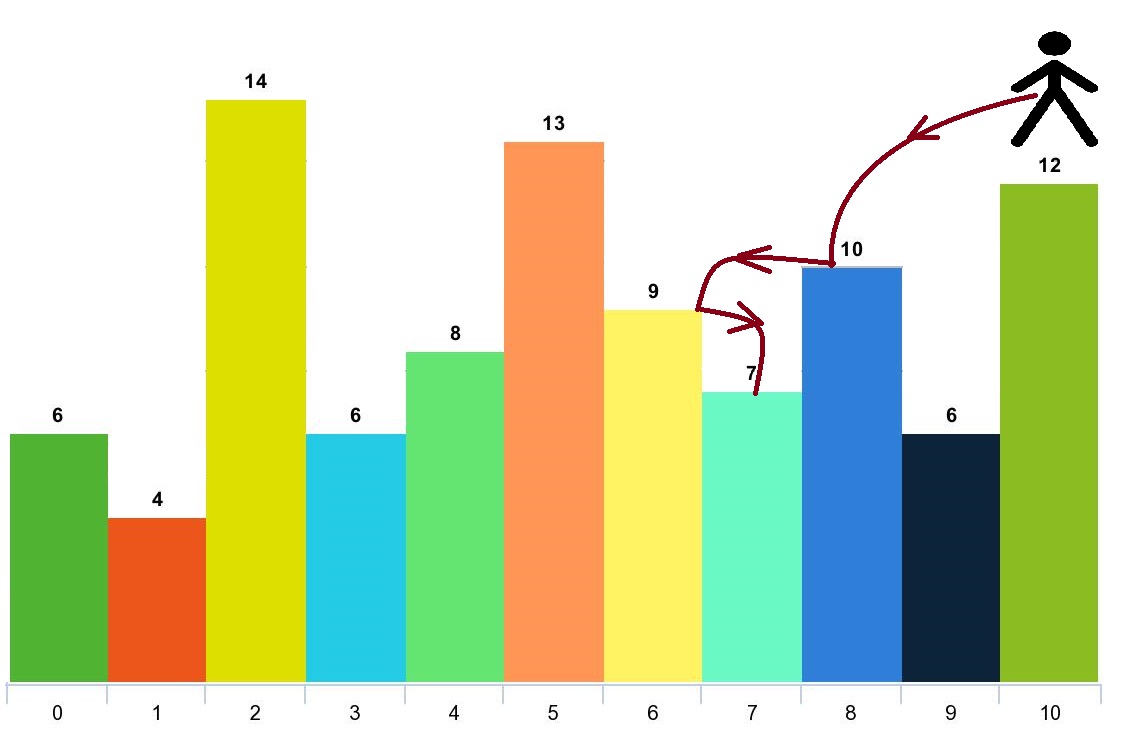
Input: arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
Output: 4
Explanation: You can start at index 10. You can jump 10 --> 8 --> 6 --> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.

Example 2:

Input: arr = [3,3,3,3,3], d = 3
Output: 1
Explanation: You can start at any index. You always cannot jump to any index.

Example 3:

Input: arr = [7,6,5,4,3,2,1], d = 1
Output: 7
Explanation: Start at index 0. You can visit all the indicies. 

Constraints:

• 1 <= arr.length <= 1000
• 1 <= arr[i] <= 105
• 1 <= d <= arr.length

题解：

Use DFS + memo. 
For each index, try to jump from this index and see how many indices it can reach.

Use memo to avoid re-comuputation.

Time Complexity: O(n*d). n = arr.length. Use the memo to and avoid re-compute. For each index, it needs O(d) time if all the reach nodes are pre-computed and saved into memo.

Space: O(n). 

AC Java:

class Solution {
    public int maxJumps(int[] arr, int d) {
        if(arr == null || arr.length == 0 || d <= 0){
            return 0;
        }

        int n = arr.length;
        int[] memo = new int[n];
        int res = 1;
        for(int i = 0; i < n; i++){
            res = Math.max(res, dfs(arr, d, i, n, memo));
        }

        return res;
    }

    private int dfs(int[] arr, int d, int i, int n, int[] memo){
        if(memo[i] != 0){
            return memo[i];
        }

        int res = 1;
        for(int j = i + 1; j <= Math.min(i + d, n - 1) && arr[j] < arr[i]; j++){
            res = Math.max(res, 1 + dfs(arr, d, j, n, memo));
        }

        for(int j = i - 1; j >= Math.max(i - d, 0) && arr[j] < arr[i]; j--){
            res = Math.max(res, 1 + dfs(arr, d, j, n, memo));
        }
        
        memo[i] = res;
        return res;
    }
}

类似Jump Game IV.