LeetCode 1443. Minimum Time to Collect All Apples in a Tree

原题链接在这里：https://leetcode.com/problems/minimum-time-to-collect-all-apples-in-a-tree/description/

题目：

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.

Example 1:

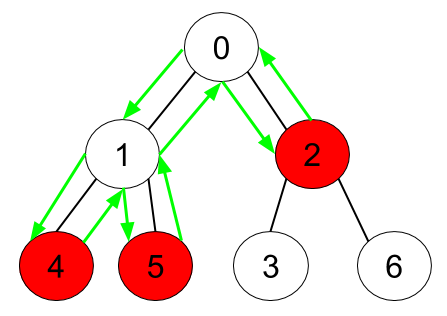
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 2:

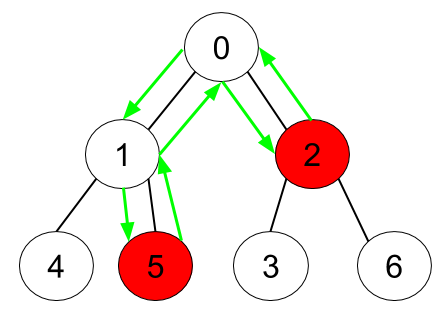
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

Constraints:

• 1 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai < bi <= n - 1
• hasApple.length == n

题解：

To get the minimum time, it needs to traverse all the subtree before it backtrack to the parent. 

e.g. 1->2->3, traverse 1->2->3 is better than 1->2->1->2->3

We first need to build the graph with edges, then perform DFS traversal.

DFS returns the minimum time for the while subtree.

DFS state needs graph, visited set, current node, current cost and hasApple boolean array.

If the current node has been visited, then return 0, that means this node is actually the parent.

For all the child, it needs to get add 2 to the next level curCost for going to the child and back.

If all the childChost is 0 and current node doesn't have a apple, then return 0.

Otherwise, return childCost + curCost.

Time Complexity: O(n). DFS takes O(v + e). since this is a tree, edges.length = n - 1.

Space: O(n).

AC Java:

class Solution {
    public int minTime(int n, int[][] edges, List<Boolean> hasApple) {
        HashMap<Integer, HashSet<Integer>> graph = new HashMap<>();
        for(int[] e : edges){
            graph.putIfAbsent(e[0], new HashSet<Integer>());
            graph.putIfAbsent(e[1], new HashSet<Integer>());
            graph.get(e[0]).add(e[1]);
            graph.get(e[1]).add(e[0]);
        }

        return dfs(graph, new HashSet<Integer>(), 0, 0, hasApple);
    }

    private int dfs(HashMap<Integer, HashSet<Integer>> graph, HashSet<Integer> visited, int cur, int curCost, List<Boolean> hasApple){
        if(visited.contains(cur)){
            return 0;
        }

        visited.add(cur);
        int childCost = 0;
        for(int child : graph.getOrDefault(cur, new HashSet<Integer>())){
            childCost += dfs(graph, visited, child, 2, hasApple);
        }

        if(childCost == 0 && !hasApple.get(cur)){
            return 0;
        }

        return childCost + curCost;
    }
}