LeetCode 834. Sum of Distances in Tree

原题链接在这里：https://leetcode.com/problems/sum-of-distances-in-tree/description/

题目：

There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given the integer n and the array edges where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

Return an array answer of length n where answer[i] is the sum of the distances between the ith node in the tree and all other nodes.

Example 1:

Input: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
Output: [8,12,6,10,10,10]
Explanation: The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer[0] = 8, and so on.

Example 2:

Input: n = 1, edges = []
Output: [0]

Example 3:

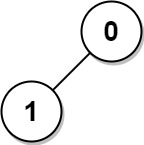
Input: n = 2, edges = [[1,0]]
Output: [1,1]

Constraints:

• 1 <= n <= 3 * 104
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• The given input represents a valid tree.

题解：

Count the sum of distance from one node, then we can simply do a DFS and it takes O(n) time. 
For all the nodes, we need O(n^2).

But we can do it with two traversal.

First DFS, bottom up. Update the count of each subtree incluing itself. count[root] += count[child].

And update sum of distance for root, res[root] += res[child] + count[child]. Why? it is like 1 -> 2 -> 3, res[2] = 1, count[2] = 2, res[1] = 3. It contains 1 to 2 and 1 to 3.

Second DFS, top down. Udpate the res for all nodes. If we move root to its child. cound[child] nodes get closer to new root, n - count[child] get further from new root.

Time Complexity: O(n). n is the number of nodes in tree. DFS takes O(n + e). But it is a tree. Thus e = n - 1.

Space: O(n).

AC Java:

class Solution {
    HashSet<Integer>[] tree;
    int [] res;
    int [] count;
    public int[] sumOfDistancesInTree(int n, int[][] edges) {
        tree = new HashSet[n];
        for(int i = 0; i < n; i++){
            tree[i] = new HashSet<Integer>();
        }
        res = new int[n];
        count = new int[n];
        for(int [] e : edges){
            tree[e[0]].add(e[1]);
            tree[e[1]].add(e[0]);
        }

        dfsCountRes(0, -1);
        dfsRes(0, -1);
        return res;
    }

    private void dfsCountRes(int root, int parent){
        for(int i : tree[root]){
            if(i == parent){
                continue;
            }

            dfsCountRes(i, root);
            count[root] += count[i];
            res[root] += res[i] + count[i];
        }

        count[root]++;
    }

    private void dfsRes(int root, int parent){
        for(int i : tree[root]){
            if(i == parent){
                continue;
            }

            res[i] = res[root] - count[i] + count.length - count[i];
            dfsRes(i, root);
        }
    }
}