LeetCode 1028. Recover a Tree From Preorder Traversal

原题链接在这里：https://leetcode.com/problems/recover-a-tree-from-preorder-traversal/description/

题目：

We run a preorder depth-first search (DFS) on the root of a binary tree.

At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node.  If the depth of a node is D, the depth of its immediate child is D + 1.  The depth of the root node is 0.

If a node has only one child, that child is guaranteed to be the left child.

Given the output traversal of this traversal, recover the tree and return its root.

Example 1:

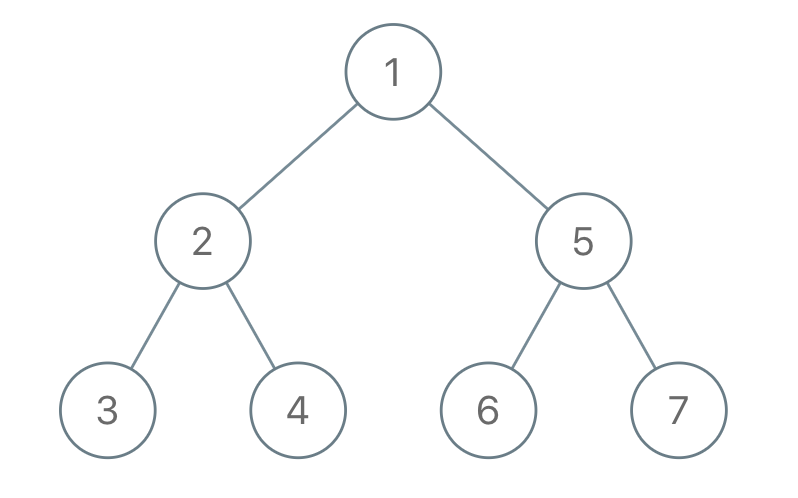
Input: traversal = "1-2--3--4-5--6--7"
Output: [1,2,5,3,4,6,7]

Example 2:

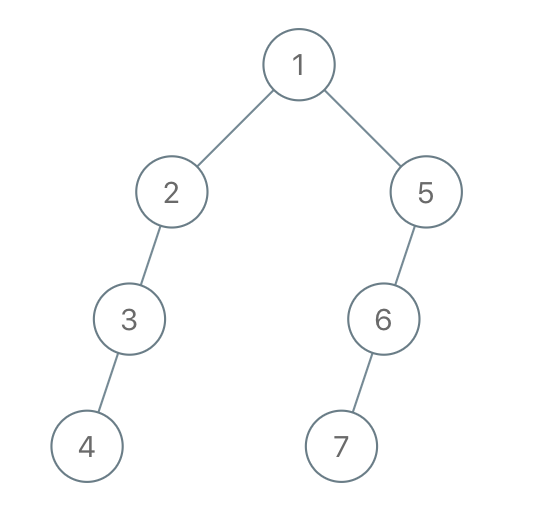
Input: traversal = "1-2--3---4-5--6---7"
Output: [1,2,5,3,null,6,null,4,null,7]

Example 3:

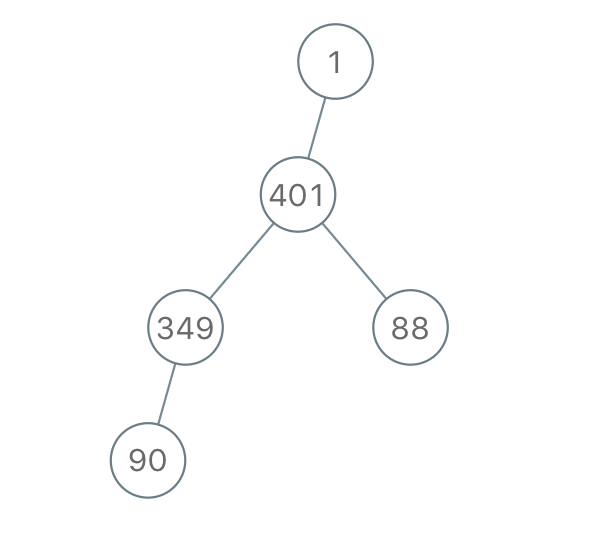
Input: traversal = "1-401--349---90--88"
Output: [1,401,null,349,88,90]

Constraints:

• The number of nodes in the original tree is in the range [1, 1000].
• 1 <= Node.val <= 109

题解：

For each number, the count of - before it means which level it belongs to.

Using a stack to maintain the trace of preorder visited node.

The first number is put into stack.

Then when we have -2, we know it is the child of root. The level is 1.

We keep popping until we have 1 node in the stack and assign 2 to its left or right child. If it doesn't have left child, assign to left. If not, assign to right.

In the end, the lasrt node in the stack is the root.

Time Complexity: O(traversal.length()). 

Space: O(h). h is the height of the tree. 

AC Java:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode recoverFromPreorder(String traversal) {
        Stack<TreeNode> stk = new Stack<>();
        int i = 0;
        while(i < traversal.length()){
            int level = 0;
            while(i < traversal.length() && traversal.charAt(i) == '-'){
                level++;
                i++;
            }

            int val = 0;
            while(i < traversal.length() && traversal.charAt(i) != '-'){
                val = val * 10 + (traversal.charAt(i) - '0');
                i++;
            }

            TreeNode node = new TreeNode(val);
            while(stk.size() > level){
                stk.pop();
            }

            if(!stk.isEmpty()){
                TreeNode top = stk.peek();
                if(top.left == null){
                    top.left = node;
                }else{
                    top.right = node;
                }
            }

            stk.push(node);
        }

        while(stk.size() > 1){
            stk.pop();
        }

        return stk.pop();
    }
}

AC Python:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def recoverFromPreorder(self, traversal: str) -> Optional[TreeNode]:
        stk = []
        i = 0
        while i < len(traversal):
            level = 0
            while i < len(traversal) and traversal[i] == '-':
                level += 1
                i += 1
            val = 0
            while i < len(traversal) and traversal[i] != '-':
                val = val * 10 + int(traversal[i])
                i += 1
            
            while len(stk) > level:
                stk.pop()
            
            node = TreeNode(val)
            if stk:
                if not stk[-1].left:
                    stk[-1].left = node
                else:
                    stk[-1].right = node
            stk.append(node)
        
        return stk[0]