LeetCode 2458. Height of Binary Tree After Subtree Removal Queries

原题链接在这里：https://leetcode.com/problems/height-of-binary-tree-after-subtree-removal-queries/

题目：

You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.

You have to perform m independent queries on the tree where in the ith query you do the following:

  • Remove the subtree rooted at the node with the value queries[i] from the tree. It is guaranteed that queries[i] will not be equal to the value of the root.

Return an array answer of size m where answer[i] is the height of the tree after performing the ith query.

Note:

  • The queries are independent, so the tree returns to its initial state after each query.
  • The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.

 

Example 1:

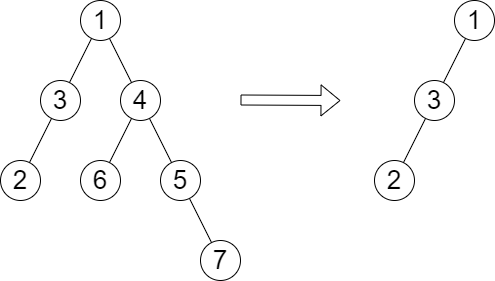
Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
Output: [2]
Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4.
The height of the tree is 2 (The path 1 -> 3 -> 2).

Example 2:

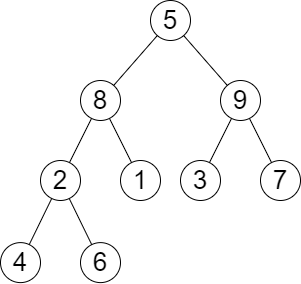
Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
Output: [3,2,3,2]
Explanation: We have the following queries:
- Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 4).
- Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 -> 8 -> 1).
- Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 6).
- Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 -> 9 -> 3).

Constraints:

  • The number of nodes in the tree is n.
  • 2 <= n <= 105
  • 1 <= Node.val <= n
  • All the values in the tree are unique.
  • m == queries.length
  • 1 <= m <= min(n, 104)
  • 1 <= queries[i] <= n
  • queries[i] != root.val

题解：

For each node, it has its depth and height.

 

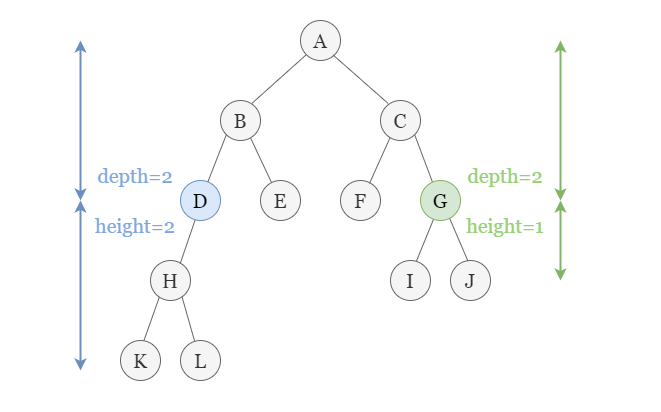
For each depth level, we maintain top 2 node with biggest height.

When removing one node, go to its depth level depth, if there is only one node, then it is going to be removed, the root height becomes depth - 1.

When it has 2 nodes on that depth level max1 and max2, if we are about to remove the biggest max1 node, then we need to use max2 height + depth as root height.

If we are not to remove the biggest max1 node, then root height is not changed.

Note: we could use minHeap to maintian top2, but since next query is working on the original tree, we need to add max1 and max2 back to minHeap.

Time Complexity: O(n + queries.length). n = total number of nodes in the tree.

Space: O(n). regardless res.

AC Java:

 1 /**
 2  * Definition for a binary tree node.
 3  * public class TreeNode {
 4  *     int val;
 5  *     TreeNode left;
 6  *     TreeNode right;
 7  *     TreeNode() {}
 8  *     TreeNode(int val) { this.val = val; }
 9  *     TreeNode(int val, TreeNode left, TreeNode right) {
10  *         this.val = val;
11  *         this.left = left;
12  *         this.right = right;
13  *     }
14  * }
15  */
16 class Solution {
17     public int[] treeQueries(TreeNode root, int[] queries) {
18         HashMap<Integer, Integer> depthHm = new HashMap<>();
19         HashMap<Integer, Integer> heightHm = new HashMap<>();
20         dfs(root, 0, depthHm, heightHm);
21         
22         // Maintain the depth and its corresponding two height node
23         HashMap<Integer, PriorityQueue<int[]>> depthToNodeHeight = new HashMap<>();
24         for(Map.Entry<Integer, Integer> entry : depthHm.entrySet()){
25             int val = entry.getKey();
26             int depth = entry.getValue();
27             depthToNodeHeight.putIfAbsent(depth, new PriorityQueue<>((a, b) -> a[1] == b[1] ? a[0] - b[0] : a[1] - b[1]));
28             depthToNodeHeight.get(depth).add(new int[]{val, heightHm.get(val)});
29             if(depthToNodeHeight.get(depth).size() > 2){
30                 depthToNodeHeight.get(depth).poll();
31             }
32         }
33         
34         int n = queries.length;
35         int [] res = new int[n];
36         int rootHeight = heightHm.get(root.val);
37         for(int i = 0; i < n; i++){
38             int dep = depthHm.get(queries[i]);
39             PriorityQueue<int []> top2 = depthToNodeHeight.get(dep);
40             if(top2.size() == 1){
41                 res[i] = dep - 1;
42                 continue;
43             }
44             
45             int [] max2 = top2.poll();
46             int [] max1 = top2.poll();
47             if(max1[0] == queries[i]){
48                 res[i] = dep + max2[1];
49             }else{
50                 res[i] = rootHeight;
51             }
52             top2.add(max1);
53             top2.add(max2);
54         }
55         
56         return res;
57     }
58     
59     private int dfs(TreeNode root, int depth, Map<Integer, Integer> depthHm, Map<Integer, Integer> heightHm){
60         if(root == null){
61             return -1;
62         }
63         
64         depthHm.put(root.val, depth);
65         int l = dfs(root.left, depth + 1, depthHm, heightHm);
66         int r = dfs(root.right, depth + 1, depthHm, heightHm);
67         int height = Math.max(l, r) + 1;
68         heightHm.put(root.val, height);
69         return height;
70     }
71 }

类似Maximum Depth of Binary Tree.

posted @ 2022-10-30 13:28  Dylan_Java_NYC  阅读(248)  评论(0)  编辑  收藏  举报