LeetCode 296. Best Meeting Point

原题链接在这里：https://leetcode.com/problems/best-meeting-point/

题目：

Given an m x n binary grid grid where each 1 marks the home of one friend, return the minimal total travel distance.

The total travel distance is the sum of the distances between the houses of the friends and the meeting point.

The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.

Example 1:

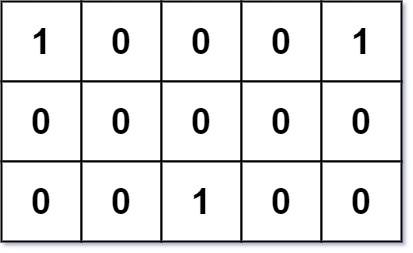
Input: grid = [[1,0,0,0,1],[0,0,0,0,0],[0,0,1,0,0]]
Output: 6
Explanation: Given three friends living at (0,0), (0,4), and (2,2).
The point (0,2) is an ideal meeting point, as the total travel distance of 2 + 2 + 2 = 6 is minimal.
So return 6.

Example 2:

Input: grid = [[1,1]]
Output: 1

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• grid[i][j] is either 0 or 1.
• There will be at least two friends in the grid.

题解：

When trying to minimize the manhattan distance, it is trying to minimize the absolute deviations of x and y.

And median minimize the absolute deviations.

We get all x and y when there is a building.

And calculate absolute deviations.

Time Complexity: O(m * n). m = grid.length. n = grid[0].length.

Space: O(m + n).

AC Java:

class Solution {
    public int minTotalDistance(int[][] grid) {
        if(grid == null || grid.length == 0 || grid[0].length == 0){
            return 0;
        }
        
        int m = grid.length;
        int n = grid[0].length;
        
        List<Integer> iIndexList = new ArrayList<>();
        for(int i = 0; i < m ; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 1){
                    iIndexList.add(i);
                }
            }
        }
        
        List<Integer> jIndexList = new ArrayList<>();
        for(int j = 0; j < n; j++){
            for(int i = 0; i < m; i++){
                if(grid[i][j] == 1){
                    jIndexList.add(j);
                }
            }
        }
        
        int iDist = dist(iIndexList);
        int jDist = dist(jIndexList);
        return iDist + jDist; 
    }
    
    private int dist(List<Integer> list){
        int l = 0;
        int r = list.size() - 1;
        int res = 0;
        
        while(l < r){
            res += list.get(r--) - list.get(l++);
        }
        
        return res;
    }
}

类似Minimum Moves to Equal Array Elements II.